Логіка - Мозгова Н.Г. - 4. Особливості імплікації

Серед формул логіки висловлювань є такі, які незалежно від значень істинності їх атомів є завжди істинними. їх називають тотожно істинними формулами або тавтологіями.

Прикладом тавтології є відомий вже вам закон виключеного третього - А V -А. Побудуємо його матрицю:

Як бачимо, незалежно від того, які значення істинності мають атоми (А, -А), формула в цілому має значення істинності - "Істина" (1).

Зазначимо, що будь-який закон логіки є тотожно істинною формулою або тавтологією.

*Дві формули F1 та F2с еквівалентними (рівносильними) тоді і тільки тоді, коли їх подвійна імплікація (F1-F2) - тавтологія.

Перевірку еквівалентності двох формул здійснюють за допомогою таблиць істинності. Якщо значення їх істинності в цілому однакові, то відповідні формули еквівалентні. Перевіримо, наприклад, чи еквівалентні такі формули:

А->Ві~А УВ

Побудуємо їх таблиці істинності:

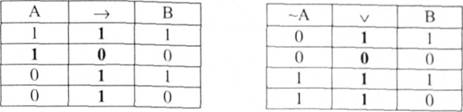
Очевидно, що подвійна імплікація цих формул є тавтологією:

(А -> В) <-* (~ А V В)

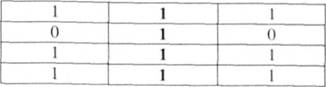
Деякими елементарними еквівалентностями логіки висловлювань є такі:

1) А—>В = ~А/В - вираження імплікації через диз'юнкцію та заперечення.

2), а) ~ (А Л В) = ~ А V - В;

Ь) ~(А/В) = ~АЛ~В- закони де Моргана.

3) А <-> В = (А —> В) Л (В —> А) - подвійна імплікація через імплікацію та кон'юнкцію.

4) Скориставшись еквівалентністю (1), отримаємо: А <-> В = (~А V В) Л (~В V А).

5) Скориставшись правилом де Моргана (2Ь), отримаємо: А <-> В н ~ (А Л ~В) Л ~(В Л -А).

Відношення еквівалентності дозволяє перетворювати одні (складні) висловлювання на інші (прості).

4. Особливості імплікації

Імплікація двох висловлювань (А та В) суттєво відрізняється від інших логічних операцій - кон'юнкції, диз'юнкції та подвійної імплікації. Якщо АЛВ = ВЛА, АУВ а ВуА, А<->В = В<->А, то А—>В Ф В->А. Тобто, якщо всі логічні операції є симетричними, то імплікація не є симетричною операцією.

Саме тому, ми давали її визначення не через випадок істинності, а через випадок хибності.

Тепер розглянемо випадки її істинності. Матриця імплікації має вигляд:

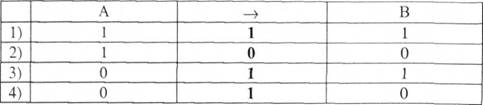
З таблиці видно, що:

1) Імплікація є завжди істинною, при хибному антецеденті, незалежно від значення істинності консеквента (рядки таблиці 3,4). В обох випадках А є хибним, але в третьому рядку В є істинним, а в 4-му В -хибне. Отже, ми можемо визначити істинність імплікації, знаючи тільки значення істинності лівої частини. Якщо вона хибна, то імплікація є істинною.

2) Імплікація є завжди істинною при істинному консеквенті (1, З рядки), незалежно від значення істинності антецедента. Так, у першому рядку він істинний, а в третьому - хибний. Це теж дозволяє визначати істинність імплікації тільки за значенням істинності консеквента.

Отже, імплікація є істинною тоді і тільки тоді, коли антецедент є хибним або консеквент є істинним.

5. Відношення логічного слідування

Дуже важливим у логіці висловлювань (і в логіці взагалі) є відношення логічного слідування, оскільки на ньому ґрунтуються всі умовиводи та доведення. Відношення логічного слідування позначають символом К Формула Б. н Б2 читається: "З Р. логічно слідує (випливає) Р2, або Р2 є логічним наслідком

З формули Р1 логічно слідує формула Р2 тоді і тільки тоді, коли їх імплікація (¥ ] —є завжди істинною формулою (* та етологією).

Між відношенням логічного слідування (Н) та імплікацією (—>) існує тісний зв'язок, але їх не слід плутати. Імплікація - це висловлювання, що складається з двох елементарних висловлювань і серед наборів її значень істинності може бути "хиба". *Логічне слідування - це відношення між двома висловлюваннями, яке є завжди істинною імплікацією.

Для перевірки, чи є Б2 логічним наслідком ¥г необхідно:

1) з'єднати їх знаком імплікації (Р,—"Р2);

2) побудувати таблицю для отриманої формули;

3) якщо ця формула є тавтологією, то з Р, логічно випливає її (Б, Ь Б2); якщо ця формула не є тавтологією, то з Б, логічно не випливає Р2

Нехай Р, - (АлВ), а Р2 - (А/В). Перевіримо, чи є ¥2 логічним наслідком Б,.

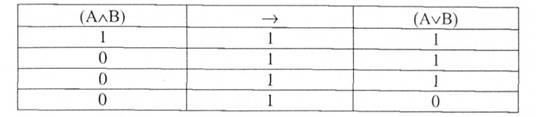
Оскільки отримана формула є тавтологією, то це означає, що Р, ьР2. Перевіримо тепер навпаки: чи є Р, логічним наслідком Р2.

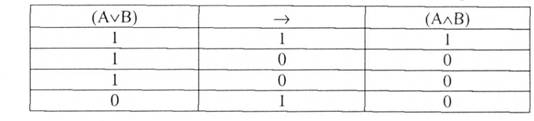
Оскільки ця формула не є тавтологією, то це означає, що Р, не є логічним наслідком з Р2

Якщо Р1ЬР2, але ¥2*¥19 то формула Р, є більш сильною по відношенню до Р2. Якщо ж Р,І-Р2 і $2і-¥1, то Р1 та Р2- рівносильні або еквівалентні.

Література для поглибленого вивчення розділу

А. Основна.

1. Гетманова А.Д. Логика. - М.: Новая школа, 1995. - С. 68-83.

2. Жеребкін В.Є. Логіка. - X.: Основа; К.: Знання, 1999. - С. 86-93.

3. Кириллов В.И., Старченко A.A. Логика. -М.: Высшая школа, 1995. -С. 158-163.

4. Конверський А.Є. Логіка. - К.: Четверта хвиля, 1998. - С. 195-202.

5. Иванов Е.А. Логика. - М: Издательство БЕК, 1996. - С. 137-171.

6. Свинцов В.И. Логика.-М.: Скорина; Весь мир, 1998.-С. 101-116.

7. Тофтул М.Г. Логіка: Навч. посібн. для студентів вищих навчальних закладів. - К.: Академія, 2003. - С. 90-102.

8. Хоменко І.В., Алексюк I.A. Основи логіки. - К.: Золоті ворота, 1996. -С. 96-145.

9. Хоменко І.В. Логіка: Підручник для студентів вищих навчальних закладів. - К.: Абрис, 2004. - С. 99-107.

В. Додаткова

1. Ивин А. А. Искусство правильно мыслить. - М.: Просвещение, 1990. -С. 154-209.

2. Карнап Р. Значение и необходимость. - М.: Наука, 1968. - С. 331-334.

3. Кондаков Н.И. Логический словарь-справочник. - М.: Наука, 1975. Статті: высказывание, дизъюнкция, импликация, исчисление высказываний, конъюнкция, отношение между суждениями, разделительное суждение, сложное суждение, суждение, условное суждение, эквивалентность.

4. Логические методы и формы научного познания. - К.: Наукова думка, 1984.-200 с.

5. Мельников В.Н. Логические задачи. - К.; Одесса: Вища школа, 1989. -С. 59-101; 154-177.

6. Свинцов В.И. Смысловой анализ и обработка текста. - М.: Наука 1979.-272 с.