Логіка - Мозгова Н.Г. - 4. Обернення судження

Умовами здобуття істинних висновків в умовиводі є: 1) істинність вихідних висловлювань або засновків; 2) правильність виводу. Поняття істинного висловлювання (судження) розглядалось нами в модулі IV - "Просте судження". Поняття ж "правильності виводу" пов'язане з відношенням логічного слідування. Для розкриття його змісту проаналізуємо таке міркування: "Якщо я склав залік з логіки (А) та залік з історії України (В), отже, я можу стверджувати, що я напевно склав залік з логіки або історії України". Логічна структура цього міркування є такою: "Якщо А і В, отже, А або В". Запишемо її у вигляді формули логіки висловлювань та побудуємо його таблицю істинності:

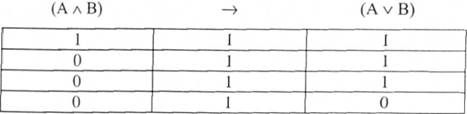
Як бачимо, формула логіки висловлювань, що відображає структуру нашого міркування, є завжди істинною формулою або тавтологією. А це, в свою чергу, означає, що між першим та другим твердженням існує відношення логічного слідування (АлВ ь А/В) - таку структуру міркування називають структурою правильного виводу. Таким чином, правильним умовивід є тоді і тільки тоді, коли висновок є логічним наслідком із засновків. У таку структуру ми можемо замість А і В поставити будь-які за змістом істинні твердження і завжди будемо отримувати істинний висновок.

Розглянемо інший приклад: "Якщо людина захворіє на грип (А), то в неї підніметься температура тіла (В). У цієї людини температура тіла підвищена (В). Отже, вона захворіла на грип (А)". Логічна структура цього міркування така:

Якщо А, то В.

В._

А.

Запишемо цю структуру у вигляді формули логіки висловлювань та перевіримо її на тавтологічність:

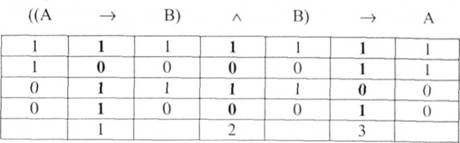
Послідовність побудови таблиці така: 1) значення істинності імплікації (А —> В); 2) значення істинності кон'юнкції ((А -" В) л В); 3) значення істинності формули в цілому (...Л В) —> А). Як бачимо, ця формула не є тавтологією. Це означає, що вона не є структурою правильного виводу і не є правильним виводом, оскільки при істинних засновках вона не завжди дає істинний висновок. Так, у нашому прикладі висновок "людина захворіла на грип" не є необхідним, бо причиною високої температури тіла можуть бути і багато інших причин (крім захворювання на грип).

Отже, неправильним називають такий умовивід, у якому між засновками та висновком не існує відношення логічного слідування. Такий умовивід не гарантує істинного висновку при істинних засновках.

4. Обернення судження

Нагадаємо, що дедуктивні умовиводи поділяються на виводи логіки висловлювань (виводи зі складних суджень) та виводи з простих категоричних суджень (А, Е, І, О), які мають структуру "Б-Р". Виводи з простих категоричних суджень поділяють на опосередковані - з двох і більше суджень-засновків, та безпосередні з одного судження-засновку.

У даному і подальших параграфах цього розділу ми будемо розглядати безпосередні умовиводи.

* Безпосередніми умовиводами називають такі дедуктивні виводи, які здійснюються з одного категоричного судження-засновку.

Існують чотири основних види безпосереднього виводу:

1) обернення судження; 2) перетворення судження; 3) протиставлення предикатові та 4) виводи за логічним квадратом.

Обернення - це логічна операція, в результаті якої Б та Р судження-засновку міняються місцями. Якість судження при оберненні не змінюється. Якщо кількість судження не змінюється, то таке обернення називають простим, або чистим. Якщо ж кількість судження при оберненні змінюється, то таке обернення називають оберненням з обмеженням (узагальненням).

Залежно від чотирьох типів простих категоричних суджень існують такі правила обернення суджень.

Загальностверджувальне судження.

А(8Р) -" А(РБ): "Усі Б є Р, отже, всі Р є 8".

Наприклад:

Це приклад чистого обернення.

А($Р) -" І(Р8): "Усі Б є Р, отже, деякі Р є Б".

Це приклад обернення з обмеженням. Загальнозаперечне судження.

Е(8Р) -" Е(Р8): "Жодне 8 не є Р, отже, жодне Р не є 8". Наприклад:

Частковостверджувальне судження. I(SP) -> I(PS): "Деякі S є Р, отже, деякі Р є S". Наприклад:

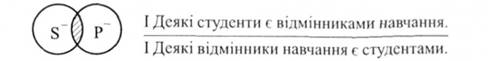
КБР) -> А(РБ): "Деякі 8 є Р, отже, всі Р є 8". Наприклад:

Це приклад обернення з узагальненням.

Частковозаперечне судження не завжди дає необхідні виводи у випадку обернення, тобто висновки обернення з судження 0(8Р) не завжди є істинними. Наприклад: "Деякі злочинці не є рецидивістами, отже, деякі рецидивісти не є злочинцями (?!)". Виходячи з цього, частковозаперечне судження операції обернення не підлягає.