Логіка - Мозгова Н.Г. - 7. Виводи за логічним квадратом

Перетворення - це логічна операція, в результаті якої судження змінює свою якість, а предикат висновку заперечує предикат засновку. Кількість судження при цьому не змінюється.

У залежності від чотирьох типів простих категоричних суджень існують такі правила перетворення суджень.

Загальностверджувальне судження.

А(8Р) —> Е(8 - Р): "Усі 8 є Р, отже, жодне 8 не є не Р".

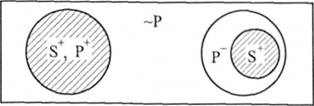
Основою утворення умовиводу тут виступає закономірність відношення обсягів двох суперечливих понять, які є предикатами одного і

того самого суб'єкта. Відомо, що два суперечливих поняття (Р і ~Р) завжди вичерпують обсяг свого родового поняття. Якщо відомо, що даний предмет входить до обсягу Р, то це є підставою для висновку, що він не входить до обсягу ~Р, і навпаки. Подвійне заперечення (не є не Р), що використовується у судженні-висновку означає рівнозначність цих двох суджень.

Наприклад:

А Усі адвокати - юристи.

Е Жоден адвокат не є не юристом.

Загальнозаперечне судження.

E(SP) -> A(S ~Р): "Жодне S не є Р, отже, всі S є не Р".

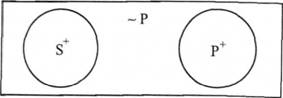
Наприклад:

Жодна кішка не є собакою. Усі кішки є не собаками.

Частковостверджувальне судження.

1(SP) —"0(S ~Р): "Деякі S є Р, отже, деякі S не є не Р".

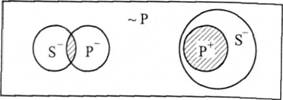
Наприклад:

Деякі студенти є відмінниками. Деякі студенти не є не відмінниками.

Частковозаперечне судження.

О(БР) -> 1(5 ~Р): "Деякі Б не є Р, отже, деякі Б є не Р".

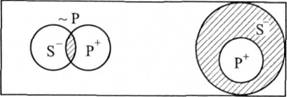
Наприклад:

Деякі жінки не є депутатами. Деякі жінки є не депутатами.

6. Протиставлення предикатові

Протиставлення предикатові - це логічна операція, яка складається з двох попередніх, тобто: 1) судження змінює якість на протилежну, а в деяких випадках змінюється і кількість судження; 2) Б та Р судження-висновку міняються місцями; 3) Р висновку є поняттям, заперечним (~Р) до Р засновку.

У залежності від чотирьох типів простих категоричних суджень існують такі правила протиставлення предикатові.

Загальностверджувальне судження.

А(8Р) —" Е(~ РБ): "Усі 8 є Р, отже, жодне не Р не є 5".

Наприклад:

Усі правильні трикутники є рівнобічними. Жоден нерівнобічний трикутник не є правильним.

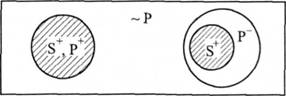
Загальнозаперечне судження.

E(SP) -> I(~PS): "Жодне S не є Р, деякі не Р є S".

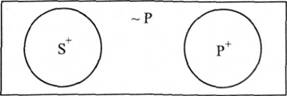
Наприклад:

Жоден кит не є рибою. Деякі не риби є китами.

Оскільки, в поняття "не риби" включається багато видів тварин (крім китів), то ми кажемо "деякі", але не "всі". Частковозаперечне судження. 0(8Р) -"І(~Р8): "Деякі 8 не є Р, отже, деякі не Р є 8 ".

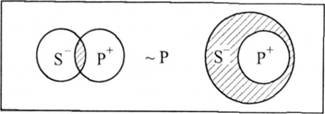
Наприклад:

Деякі злочинці не є повнолітніми. Деякі неповнолітні є злочинцями.

Частковостверджувальне судження не завжди дає необхідні виводи при протиставленні предикатові, тобто висновки з протиставлення предикатові судження І(8Р) не завжди є істинними (а часто навіть позбавлені здорового глузду). Наприклад: "Деякі люди є вегетаріанцями, отже, деякі невегетаріанці не є людьми (?!)". Виходячи з цього, частково-стверджувальне судження протиставленню предикатові не підлягає.

7. Виводи за логічним квадратом

Знаючи типи та характер відношень простих категоричних суджень за значенням їх істинності, можна робити достовірні умовиводи з будь-якого категоричного судження.

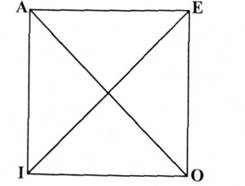
Нагадаємо, що за логічним квадратом існують такі типи відношень між категоричними судженнями:

1) Відношення протилежності (А - Е) - ці судження не можуть бути одночасно істинними.

2) Відношення часткової сумісності (І - О) - вони не можуть бути одночасно хибними.

3) Відношення підпорядкування (А - І, Е - О) - якщо загальне судження істинне (А, Е), то часткове (І, О) не може бути хибним. Інакше це відношення називають відношенням логічного слідування.

4) Відношення суперечності (А - О, Е -1) - якщо одне з них істинне, то інше (суперечливе) необхідно хибне, і навпаки.

Для того, щоб зробити умовиводи за логічним квадратом, необхідно:

1) Визначити тип судження-засновку та значення його істинності.

2) Сформулювати три інші типи суджень з тими ж самими 8 та Р та визначити значення істинності отриманих суджень-висновків.

3) Перевірити відповідність їх значень істинності при встановленні чотирьох типів відношень між судженнями.

Наприклад:

1) Судження-засновок: "Усі студенти-юристи вивчають логіку" -А(8Р), істинне.

2) Е(8Р) - "Жоден студент-юрист не вивчає логіку" - хибне; І(8Р) - "Деякі студенти-юристи вивчають логіку" - істинне; 0(8Р) - "Деякі студенти-юристи не вивчають логіку" - хибне.

Подивимось на відношення:

a) протилежність - А (істина) - Е (хиба);

b) часткова сумісність - І (істина) - О (хиба);

c) підпорядкування - А (істина) - І (істина), Е (хиба) - О (хиба); сі) суперечність - А (істина) - О (хиба), Е (хиба) -1 (істина). Оскільки значення істинності цих пар суджень відповідає визначенням логічних відношень між ними, то виводи зроблено правильно.

Література для поглибленого вивчення розділу

A. Основна.

1. Гетманова А.Д. Логика. - М.: Новая школа, 1995.-С. 121-136.

2. ЖеребкінВ.Є.Логіка.-X.:Основа;К.:Знання, 1999.-С. 108-134.

3. Кириллов В.И., Старченко А.А. Логика. - М.: Высшая школа, 1995. -С. 120-143.

4. Конверський А.Є. Логіка. - К.: Четверта хвиля, 1998. - С. 228-239.

5. Иванов Е.А. Логика. - М.: Издательство БЕК, 1996. - С. 173-200.

6. Свинцов В.И.Логика.-М.: Скорина; Весь мир, 1998.-С. 203-231.

7. Тофтул М.Г. Логіка: Навч. посібн. для студентів вищих навчальних закладів. - К.: Академія, 2003. - С. 162-169.

8. Хоменко І.В.,АлексюкІ.А. Основи логіки.-К.: Золоті ворота, 1996. -С. 96-145.

9. Хоменко І.В. Логіка: Підручник для студентів вищих навчальних закладів. - К.: Абрис, 2004. - С. 143-148.

B. Додаткова.

1. Ивин А.А. Искусство правильно мыслить. - М.: Просвещение, 1990. - С. 6-57.

2. Кондаков Н.И. Логический словарь-справочник. - М: Наука, 1975. -Статті: выведение, дедукция, непосредственное умозаключение, обращение, превращение, противопоставление предикату, умозаключение, энтимема, эпихейрема та інші статті до даної теми.

3. Логические методы и формы научного познания. - К.: Наукова думка, 1984.-200 с.

4. Мельников В.Н. Логические задачи. -К.; Одесса: Вища школа, 1989. -С. 292-314.

5. Шейко О.М. Скорочений силогізм. - К.: Вища школа, 1962. - 28 с.