Менеджмент организаций - Киржнер Л.А. - Построение модели оптимального планирования

Решение практических задач связано с тремя основными этапами исследования: составление экономико-математической модели, определение оптимального решения математическими методами, анализ полученного решения.

При выполнении первого этапа должны быть решены следующие основные проблемы: определена цель исследования, выявлены основные ограничения и осуществлено количественное выражение всех данных задач.

1. Цель исследования характеризуется признаком (критерием), по которому будут сравниваться различные варианты решения и выбирается среди них наилучшее, т. е. "оптимальное" решение.

2. Ограничения. Постановка задач линейного программирования предполагает наличие ограниченных ресурсов, которыми и необходимо распорядиться определенным образом. Поэтому необходимо определить, какие ресурсы в настоящее время являются для изучаемой проблемы решающими и, в то же время, лимитирующими, какой запас этих ресурсов. Кроме того, должны быть определены затраты каждого ресурса при том или ином варианте решения.

3. Количественное выражение всех данных задачи. Перейдем к рассмотрению критерия оптимальности. В качестве критерия оптимальности выступают показатели эффективности производства. Их очень много: наибольший рост производительности труда, наибольшая прибыль, рентабельность, показатели ритмичности работы предприятия и др. Например, ставится задача получить максимальный выпуск продукции, необходимой рынку при минимальных затратах на производство этой продукции, такая цель является наиболее характерной в настоящее время, но к решению такой задачи нужно подходить осторожно: желая снизить затраты, мы снижаем качество продукции, если качество плохое, снижается цена и т.д.

В качестве критерия оптимальности могут быть использованы показатели соотношения прибыли к численности работающих, достижение определенного результата в минимальное время, наименьшие отходы производства.

Каждый из указанных критериев имеет достаточные экономические основания для выбора в качестве критерия, и порою бывает трудно отдать предпочтение хотя бы одному из них. Проблема выбора единого критерия — это по существу проблема выбора универсального показателя оценки деятельности предприятия. Такого обобщенного показателя нет. Сложный производственный процесс может быть полно охарактеризован целой системой показателей. Но в каждой конкретной задаче может быть выбран тот из показателей, который в данном случае является наиболее существенным.

Все перечисленные выше критерии носят частичный или локальный характер в том смысле, что они отражают какую-то одну сторону производственного процесса и пригодны для использования в отдельных звеньях народного хозяйства.

В целом же на уровне народного хозяйства нужен общий критерий оптимальности. В качестве такого критерия может быть принят максимум роста национального дохода в расчете на душу населения, взятый в перспективе.

При решении задач оптимального планирования всегда возникает вопрос о числе критериев оптимальности. Применяемые математические методы решения такого рода задач обеспечивают только один критерий — либо максимум, либо минимум выбранного показателя. Но рассматривая этот вопрос с экономической точки зрения, приходим к выводу, что не всегда максимум роста одного показателя означает максимум роста другого, может быть как раз наоборот, т.е. экономически нас интересует оптимизация в одной задаче ряда различных показателей. Эта проблема является довольно сложной. Решают ее частично, идя двумя путями. Первый—стремятся к выбору такого критерия, который был бы для данного предприятия наиболее обобщающим: второй - производят оптимизацию решений по различным критериям (например, находят максимум производительности труда, затем минимум себестоимости, потом максимум прибыли), и затем путем сопоставления выбирают окончательно оптимальный вариант. Следует предупредить, что идти вторым путем необходимо очень осторожно: можно требовать экстремализации одной функции, включая постепенно остальные в систему ограничений задачи.

Математическим выражением критерия оптимальности является целевая функция

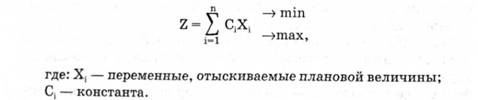
В отличие от целевой функции ограничительные условия имеют несколько другое содержание — они должны отражать те реальные условия работы предприятий, в которых составляется оптимальный план.

При решении той или иной задачи необходимо правильно определить какие ресурсы в настоящий момент являются лимитирующими, каков запас этих ресурсов, каковы затраты каждого ресурса при том или ином варианте решения. Различают несколько групп ограничений:

Первая группа — ресурсные

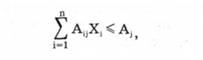
Вторая группа — ограничения комплектности, технологические (технические). Эти ограничения показывают, в каких соотношениях должны быть получены те или иные изделия. Например, если обозначить выпуск кузовов на автомобильном заводе через X,, а выпуск колес через Х2, то соотношение выпускаемой продукции составит 1:4 или Х2 = 4Х2

Третья группа — плановые ограничения. Эта группа ограничений связана с тем, что каждое предприятие, оптимизируя свой план, должно построить его с учетом требований рынка.

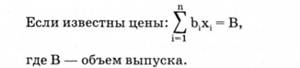
Математически ограничительные условия могут быть представлены неравенствами — левосторонними, правосторонними, а также уравнениями. Все ограничения задачи должны быть не противоречивыми, т. е. должно существовать хотя бы одно решение задачи.

Для решения задач линейного программирования в настоящее время используется достаточно богатый арсенал математических приемов и методов. Все эти методы различаются по принципам нахождения оптимальных вариантов плана, по их применяемости в решении экономических задач, по эффективности в вычислительном отношении (имеется в виду наличие эффективного алгоритма целенаправленного перебора). Но в основе всех этих методов лежит принцип последовательного улучшения плана от опорного к оптимальному. При этом используются два различных способа отыскания оптимального варианта программы.

При использовании первого способа вначале получают допустимый вариант, оптимальность достигается за определенное число итераций путем последовательного улучшения опорного плана.

При втором способе получают условно-оптимальный вариант плана, который обеспечивает максимум (минимум) целевой функции, но может не быть допустимым и становится допустимым вариантом лишь после проведения определенных преобразований.

Математический аппарат, применяемый при решении задач линейного программирования делится на три группы.

К первой группе относятся универсальные методы, с помощью которых решаются любые задачи линейного программирования. Прежде всего это метод последовательного улучшения плана с его различными модификациями. Этот метод получил название симплекс-метод.

К этой же группе относится и метод разрешающих множителей, разработанный академиком Л. В. Канторовичем (1939).

Ко второй относятся специальные методы, которые используются для решения конкретных типов задач. Главная особенность этих методов состоит в том, что они являются более простыми, чем универсальные. Наиболее широким классом таких задач являются так называемые транспортные задачи. Для решения этих задач предложено ряд методов. Наибольший практический интерес представляют два метода — распределительный и метод потенциалов, основанные на той же идее последовательного улучшения плана, что и симплексный метод, но учитывающий специфические свойства математической модели транспортной задачи.

Кроме этих методов, еще применяются приближенные методы. Они не гарантируют оптимального решения задачи, но дают хорошее приближение к оптимуму. Эти методы могут быть использованы при решении задач вручную. Сюда относится индексный метод, метод аппроксимации Фогеля и др.

В общем виде задача линейного программирования формулируется следующим образом:

Найти максимальное (минимальное) значение целей функции

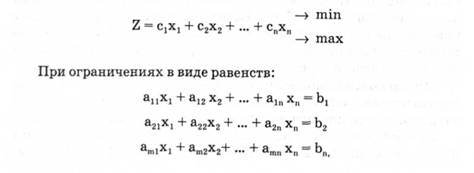
Для решения задачи методами линейного программирования задаваемые ограничения в виде неравенств должны быть преобразованы в уравнения. Такой вид записи задачи линейного программирования называется канонической задачей линейного программирования. Если неравенство указанного выше вида

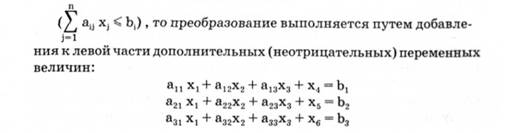
Экономический смысл дополнительных переменных состоит в том, что они характеризуют величину неиспользованного ресурса.

Ecли заданные ограничения имеют форму неравенства такого вида:

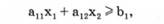
то для преобразования этих неравенств в уравнения необходимо каждый член неравенства умножить на —1 и к левой части прибавить дополнительные переменные. Для приведенного неравенства уравнение будет иметь вид:

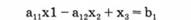
Так при составлении плана необходимо учитывать выделенные материальные ресурсы, сумма произведений количества изделий (неизвестные величины при решении задачи) на удельную норму расхода материала на каждое из изделий не может превысить величину имеющихся ресурсов.

Заданные ограничения в общем виде можно записать в форме неравенств:

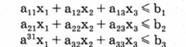
Количество выпускаемых изделий не может быть отрицательным, следовательно,

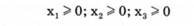
Требуется найти такие значения х1( х2, х3, которые обеспечивали бы максимальную дополнительную прибыль:

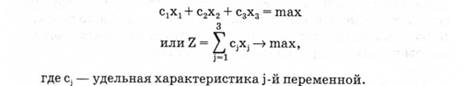
В качестве этой характеристики может выступать оптовая цена единицы j-го изделия, нормативная трудоемкость его обработки и т.д. От выбранного критерия оптимальности будет зависеть система ограничительных условий. Например, если в качестве критерия выбрано максимальное удовлетворение потребности рынка в продукции, выпускаемой предприятием, то в качестве ограничений могут выступать такие показатели, как верхний и нижний пределы допустимых переменных: Nj— нижний предел регламентирует минимально возможное количество выпускаемых j-х изделий (обращение к такому ограничительному условию будет исключать дефицит в рассматриваемом изделии);

Nj — верхний предел регламентирует максимально допустимое количество выпускаемых изделий (такое условие поможет избежать затоваривания продукцией, имеющей ограниченный сбыт)

При решении задачи календарного планирования — формирование производственной программы на короткие плановые периоды — может стоять проблема оптимизации распределения программы внутрипланового периода (по кварталам, месяцам, декадам) по критерию, например, равномерности загрузки оборудования и равномерности распределения изделий по стоимости в разрезе каждого из календарных отрезков времени.

Оптимальный план распределения производственной программы должен отвечать, по крайней мере, следующим условиям:

— соблюдение сроков выпуска изделий;

— равномерный или равномерно возрастающий объем выпуска в ценностном выражении;

— равномерная загрузка ведущих групп оборудования в каждом коротком плановом периоде;

-— обеспечение наивысшей серийности производства.

В реальных производственных условиях не всегда четко можно выделить какой-либо из критериев, поэтому приходится решать данную задачу последовательно, перебирая те или иные критерии. Затем полученные результаты сравниваются и выбирается наилучший с точки зрения учета интересов производителя и потребителя и наилучшего использования всех видов ресурсов.

При решении задач оптимального распределения программы выпуска по коротким плановым периодам модель производственной системы — целевая функция и ограничительные условия формируются для каждого из коротких периодов. В качестве ограничительных условий могут быть использованы не только ресурсные, но и стоимостные, допустимое отклонение выпуска продукции в стоимостном выражении от средней величины, от достигнутого уровня и т.п.

К типовым задачам линейного программирования относятся задачи на раскрой материалов, задачи о наилучшем составе смеси, об оптимальном плане выпуска продукции, о планировании перевозок (транспортная задача), о планировании размещения перевозок и др.