Менеджмент организаций - Киржнер Л.А. - 6.6. Модели теории игр

Анализ математической стороны и основных принципов теории игр был дан Джоном фон Нейманом еще в 1928 году. В этой ранней работе Нейман не разбирал практические приложения задач, сосредоточив основное внимание на логических основах квантовой механики. В1944 году фон Нейман и Моргенштерн опубликовали свою хорошо известную работу "Теория игр и экономического поведения", положившую начало бурному развитию математического исследования игр. Эта работа явилась основным толчком для развития линейного программирования и теории статистических решений Вальда. Она открыла также новый подход к задачам выбора решений в конкурентных ситуациях. За последние годы появилось несколько книг по теории игр. В книге "Введение в теорию игр" Маккинси дает прекрасный математический анализ общей теории с основным упором на игры двух лиц. Он рассматривает связь теории игр с линейным программированием и теорией статистических решений.

Природа игр

В каждой игре есть цель или конечное состояние, к которому стремятся игроки, выбирая направления допустимых по правилам игры действий. В некоторых случаях смысл игры заключается в достижении цели с наибольшей эффективностью. Эффективность может измеряться счетом, как в гольфе и бейсболе.

Игры с одним участником — игры без конкуренции. Участник играет на счет или для достижения цели.

Нас интересуют игры с конкуренцией. Конкурентная игра — это такая игра, где существует конечное состояние (выигрыш), которого добивается каждый игрок, но не каждый может его добиться. Таким образом, по отношению к этой цели игроки находятся в противоречии. Но, благодаря правилам игры, это противоречие приводит к общему направлению действий. Каждый игрок имеет множество ходов. Выбрать один из них — значит сделать ход. Партия — это последовательность или множество ходов, которые приводят игру к конечному состоянию.

Во многих играх достижение цели (Z) сопровождается каким-нибудь выигрышем, в частности, денежным. Эти выигрыши и проигрыши (отрицательные выигрыши) являются в некотором смысле способом счета игры, т.е. служат выражением эффективности.

Игра с нулевой суммой — это такая игра, в которой сумма выигрышей участников после конца игры равна нулю.

Стратегия — это установленный игроком метод выбора ходов в течение игры. Таким образом, стратегия — это совокупность правил выбора решения.

Платежная матрица — это таблица, которая определяет, какие платежи должны быть сделаны после завершения игры.

Теория игр не пытается описывать, как могла бы быть проведена игра. Она содержит процедуру и принципы, при помощи которых можно отбирать партии. В действительности теория игр является теорией принятия решений, применимой к конкурентным ситуациям.

Прямоугольные игры

Пример. Игрок А имеет три возможных плана игры (чистая стратегия): Р, Q, R. Игрок В имеет два возможных плана игры: S, Т.

Правила игры устанавливают, что в соответствии с выбранными планами приводятся следующие платежи.

Табл. 6.2.

Какова оптимальная стратегия для игроков А и В в этой игре?

Правила платежей удобно записать в матричной форме. Пусть положительное число показывает выигрыш игрока А, а отрицательное число показывает выигрыш игрока В. Тогда мы имеем платежную "матрицу" (рис. 6.4)

Рис. 6.4.

Рассмотрим игрока В. Очевидно, что план Т для него невыгоден. Если он выбирает этот план, он всегда проигрывает. Таким образом, его оптимальная стратегия — всегда выбирать план S. В худшем случае (когда А выберет план R) он проиграет 1 грн.

Теперь обратимся к игроку А. Ему достанется наибольший выигрыш, если он выберет план Q, а В выберет план Т. Но вряд ли это произойдет, т.к. из-за предыдущих рассуждений В никогда не выберет план Т. То лучшее, что может сделать А (если выберет S),— это выбрать план R, в этом случае игрок А выиграет 1 грн.

Таким образом, мы нашли полное решение игры. Кроме того, при этом решении игрок А выигрывает 1 грн, а игрок В проигрывает 1 грн. В этом случае 1 грн является ценой игры.

Такая игра называется прямоугольной игрой, так как ее матрица выигрышей прямоугольная. Чтобы получить решение прямоугольной игры, необходимо найти оптимальное решение, т.е. определить:

1. Оптимальные стратегии для двух игроков.

2. Цену игры.

Принцип минимакса и максимина

Пример. Рассмотрим платежную матрицу прямоугольной игры.

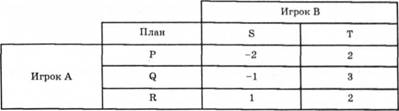
Рис. 6.5.

Решим задачу, пользуясь рассуждениями по предыдущему примеру (рис. 6.5 ).

М е т о д 1. Игрок А никогда не выберет план Р, т.к. он всегда с большим успехом может выбирать Q или план R. Учитывая это, игрок В не может вообще принимать расчет в план Р. В этом случае, очевидно, он не выберет Т, так как для него всегда выбор S выгоднее. В свою очередь, А основывается на том, что В выберет S, и, таким образом, его лучшая политика в игре — план R. Итак, мы пришли к решению.

Оптимальная стратегия игрока А: план R.

Оптимальная стратегия игрока В: план S.

Цена игры для А: 1 грн (выигрыш).

Цена игры для В: 1 грн (проигрыш).

М е т о д 2. Теперь рассмотрим следующие рассуждения.

Игрок А:

При плане Р его наименьший (min) выигрыш — 4 грн.

При плане Q его наименьший (min) выигрыш - 1 грн.

При плане R его наименьший (min) выигрыш +1 грн.

Наибольший (max) из наименьших (min) возможных выигрышей 1 грн. Значит, мы можем сказать, что "максимин для А" равен одной гривне (что соответствует выборам R, S).

Игрок В:

При плане S его наибольший (максимум) проигрыш 1 грн.

При плате Т его наибольший (максимум) проигрыш 3 грн.

Таким образом, (минимум) из наибольших проигрышей -1 грн. Мы говорим, что " минимакс для В" равен 1 грн (что опять соответствует выборам R, S).

В математических обозначениях "максимин" для А записывается выражением max(i) min(j) aij

Седловые точки

Не всякая прямоугольная игра приводит к решениям с единственным оптимальным выбором для обоих игроков А и В. Например, задана платежная матрица (рис. 6.6.)

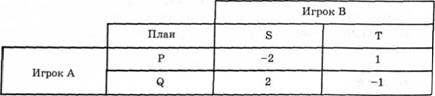
Рис. 6.6.

Если А берет план Р1, то В, очевидно выберет план S. Если А выберет план Q, то В выберет план Т. Мы видим, для А нет определенного лучшего плана. То же можно сказать и об игроке В.

Используя принципы минимакса, находим:

Максимин для А = -1 грн (выбор Q, Т);

Наиболее легкий прием отыскания седловой точки заключается в определении числа, наименьшего из всех чисел своей строки и наибольшего из числа своего столбца. Если такого числа нет, то нет и седловой точки. Стратегии игроков, соответствующие найденному числу,— оптимальные стратегии игроков, а найденное число — цена игры. Если существует два или больше таких чисел, то имеется два или более решений. Каждое решение соответствует седловой точке.