Стратегічний менеджмент - Осовська Г.В. - Моделювання

Модель являє собою спрощений образ дійсності. Моделі охоплюють, як правило, не всі ознаки та зв'язки оригіналу, що відображається, а лише ті,які, на погляд дослідника, є важливими в умовах конкретної постановки проблеми.

Створення аналітичних моделей передбачає запис рівностей, що характеризують залежність однієї змінної від тих чи інших факторів. Іншими словами, в аналітичних моделях функціональна залежність набуває визначеного вигляду. Такі моделі можуть бути однофакторними і багато-факторними [Федосеев].

Розглянемо аналітичні моделі попиту на прикладі лінійно-кореляційно-регресивних статистичних моделей, що базуються на конкретних даних дослідження сімей. В таблиці 10.2 подані статистичні дані за 1999 р. про витрати на харчування, грошові доходи та споживання молочних продуктів у розрізі домогосподарств з різними сукупними середньодушовими витратами.

Таблиця 10.2. Вихідні дані для побудови економічної моделі

Розглянемо двофакторну лінійну модель залежності витрат на харчування (у) від величини грошових доходів домогосподарств (х,) та споживання молочних продуктів (х^). Множинний (багатофакторний) кореляційно-регресивний аналіз вирішує три завдання: визначає форму зв'язку результативної ознаки з факторною; визначає тісноту цього зв'язку та встановлює вплив окремих факторів. В нашому випадку теоретична модель має вигляд:

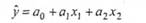
Параметри моделі а0, а,, а2 знаходять шляхом вирішення системи нормальних рівнянь:

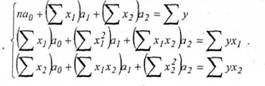
Використовуючи дані таблиці, отримаємо систему нормальних рівнянь у вигляді:

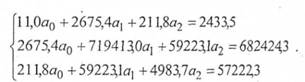
Вирішуючи цю систему (наприклад, за допомогою формул Крамера), отримаємо: а0= (-58,6); а, = 0,8; а2= 5,1. Отже, теоретична модель має вигляд:

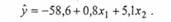
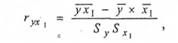
Для визначення тісноти зв'язку попередньо розраховуються парні коефіцієнти кореляції гух1, гух2, гх]х2. Наприклад, де риска над символом означає середню арифметичну, а Sуi Sxl - середньоквадратичні похибки, що відповідають вибіркам з таблиці 10.1.

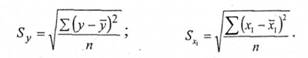
Аналогічний вигляд мають формули для і гх1х2

В нашому прикладі встановлено, що коефіцієнт кореляції г р, який характеризує залежність витрат на харчування від грошових доходів, дорівнює 0,995; коефіцієнт що показує залежність витрат на харчування від споживання молочних продуктів, дорівнює 0,992; а коефіцієнт гх/х2- залежність споживання молочних продуктів від грошових доходів складає 0,977. Отже, встановлені залежності є досить суттєвими і забезпечують надійність подальших розрахунків.

Після цього розраховується коефіцієнт множинної кореляції:

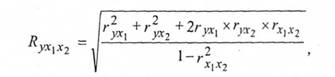
який коливається в межах від 0 до 1; чим ближче він до одиниці, тим більше враховані фактори, що діють на результативну ознаку.

В нашому прикладі розрахунки дають таке значення коефіцієнту множинної кореляції:

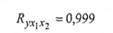
Тобто зв'язок витрат на харчування залежно від величини грошових доходів та величини споживання молочних продуктів є дуже високим.

Величина R2х,х2 називається сукупним коефіцієнтом детермінації та показує частку варіації результативної ознаки під впливом досліджуваних факторних ознак. В нашому прикладі ця величина дорівнює 0,999; це означає, що сумісний вплив грошових доходів та величини споживання молочних продуктів пояснює 99,9 % змін витрат на харчування.

Завдання аналізу тісноти зв'язку між результативним та однією із факторних ознак при незмінних значеннях інших факторів вирішується в багатофакторних моделях за допомогою одиничного коефіцієнта кореляції. Так, одиничний коефіцієнт кореляції між результативною ознакою у та факторною ознакою хІ при незмінному значенні факторної ознаки х2 розраховується за формулою:

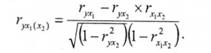
В нашому прикладі одиничні коефіцієнти кореляції витрат на харчування від грошових доходів і споживання молочних продуктів складають:

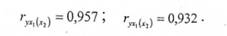
Тобто тісність зв'язку витрат на харчування з одним із досліджуваних факторів при незмінному значенні іншого досить велика, але більш тіснішим є зв'язок між витратами на харчування та загальними грошовими доходами.

Якщо одиничні коефіцієнти кореляції піднести до квадрату, то отримуємо одиничні коефіцієнти детермінації, що показують частку варіації результативної ознаки під впливом одного з факторів при незмінному значенні іншого фактору. В нашому прикладі:

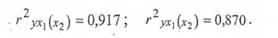
Тобто вплив грошових доходів при незмінному споживанні молочних продуктів пояснює майже 92 % змін витрат на харчування, а зміна споживання молочних продуктів при незмінних грошових доходах пояснює 87 % змін витрат на харчування.

Вплив окремих факторів у багатофакторних моделях може бути охарактеризований за допомогою одиничних коефіцієнтів еластичності, які у випадку лінійної двофакторної моделі розраховуються за формулами:

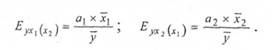
Одиничні коефіцієнти еластичності показують, на скільки відсотків зміниться результативна ознака, якщо значення однієї з факторних ознак зміниться на 1 %, а значення іншої факторної ознаки залишиться без змін.

В нашому прикладі:

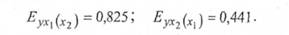
Це означає, що при збільшенні грошових доходів на 1 % та незмінному споживанні молочних продуктів, витрати на харчування збільшаться на 82,5 %; а збільшення (умовне) на 1 % споживання молочних продуктів при незмінних грошових доходах призведе до зростання витрат на харчування на 44,1 %.