Математичне програмування
Дослідження різноманітних процесів, в т.ч. й економічних, як правило, починається з їх моделювання, тобто відображення реального процесу через математичне співвідношення. При цьому складають рівняння чи нерівності, які пов'язують різні показники процесу, що досліджується і складають систему обмежень. У цих співвідношеннях виділяють такі змінні, перетворюючи які можна отримати оптимальне значення основного показника всієї системи (прибуток, доход, затрати). Відповідні методи узагальнюються під назвою "математичне програмування" або "методи дослідження операцій".
Найширше застосування в економіці знаходять такі методи:
- лінійне програмування, що дозволяє сформулювати завдання оптимізації у вигляді лінійних обмежень і лінійної цільової функції;
- динамічне програмування, розраховане на вирішення багатоступеневих завдань оптимізації;
- цілочисельне програмування, яке дозволяє вирішити оптимізаційні завдання, в тому числі завдання оптимального розподілу ресурсів.
Поняття та галузь застосування
Лінійне програмування є розділом математичного програмування, дисципліни, що присвячена теорії та методам розв'язання задач знаходження екстремуму функції від багатьох змінних, на які накладаються лінійні або нелінійні обмеження. Коли цільова функція та обмеження спрямовані на змінні лінійні, то маємо найбільш розроблене на практиці лінійне програмування.
Лінійне програмування як найбільш сприятливий (найменші затрати, максимальні прибутки тощо, при інших рівних умовах) математичний метод поміж інших альтернативних рішень застосовується для вирішення таких економічних проблем, як розробка найбільш вигідного асортименту при обмежених ресурсах, розрахунок оптимальної величини товарних запасів, планування маршрутів руху збутових агентів, вибір виробничої програми, планування перевезень (транспортна задача).
Розглянемо застосування лінійного програмування в процесі внутрішнього планування роботи підприємства на прикладі типової задачі про використання та оцінку ресурсів.
Концептуальний підхід
Нехай на випуск п видів продукції П,...Пп витрачається т видів ресурсів (сировина, матеріали, трудові ресурси тощо) А,...Ат. Відомі витрати а., ресурсів /-го виду на одиницю продукції у'-го виду, обсяг Ь, ресурсів і-го виду і величина прибутку с. від реалізації одиниці продукції .і-го виду. Треба так організувати випуск продукції, виходячи з наявних ресурсів, щоб одержати найбільший прибуток. Дані задачі записуємо в таблицю 10.3.
Для розв'язання задачі складають її математичну модель, тобто виражаємо умови задачі в математичній формі. Введемо шукані невідомі хг..хп - кількості одиниць випущеної продукції відповідно видів ПГ..П .
Таблиця 10.3
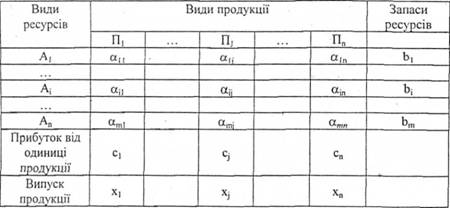
Невідомі хг..хп мають задовольняти таку систему нерівностей:
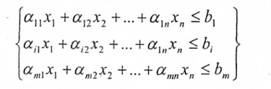
Кожна з нерівностей показує, що фактичні витрати відповідного виду . ресурсів мають не перевищувати наявний його обсяг. Виходячи з економічного змісту задачі, невідомі хґ..хя можуть набувати лише невід'ємних значень, тобто:
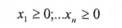
Прибуток від випуску всієї продукції становить:
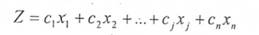
Загальні характеристики
Вирішення завдань внутрішнього планування роботи підприємства в основному базується на застосуванні симплекс-методу. Цей метод був розроблений в кінці 40-х років американським математиком Данцигом і може бути використаний для вирішення комплексу завдань: формування специфічної річної виробничої програми випуску підприємством, план завантаження різних груп устаткування, календарний розподіл виробничої програми випуску, розподіл річної програми випуску за кварталами, місяцями, декадами.
Основна ідея симплекс-методу полягає ось у чому:
1) приймається за базу одна з можливих програм - опорний план;
2) здійснюється його покрокове покращання, поки не буде отриманий оптимум за визначеною критеріальною функцією.
Таким чином, проблема полягає у визначенні опорного варіанта програми та знаходження способу поліпшення останнього. При цьому для формування початкового варіанта програми створюється наче запас, можливість реалізації у вигляді резервів тих ресурсів, які регламентуються в конкретній виробничій ситуації. В процесі перетворень (ітерацій) одні змінні переводяться в план, інші - виключаються з нього. З кожним кроком план наближається до оптимального і в кінцевому підсумку приходить до нього, якщо в умовах задачі немає протиріч.
Вирішення задач симплекс-методом передбачає виконання таких процедур (мал. 10.3).
Для конкретного підприємства можна сформувати різні варіанти плану виробництва. При цьому необхідні для його виконання ресурси та отримані від його реалізації результати будуть різними. Один варіант плану з точки зору досягнення величини будь-якого із показників або дотримання виконання певних умов буде кращий, а інший - гірший.
Необхідною умовою постановки задачі лінійного програмування є обмеження на наявні ресурси, на величину попиту, на виробничу потужність та інші фактори. Іншою умовою постановки й вирішення планової задачі методами лінійного програмування є вибір критерію оптимальності плану, що виражений кількісно.
Критерій оптимальності повинен задовольняти таким вимогам: 1) бути єдиним, тобто одним для даної задачі; 2) кількісно вимірним. І, нарешті, важливою умовою є лінійна залежність між різними невідомими величинами (змінними), що використовуються в задачі.
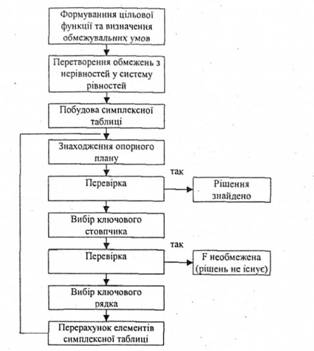
Мал. 10.3. Процедури симплекс-методу
Приклад застосування
Торгове підприємство для продажу товарів трьох видів використовує такі ресурси: нас і площа торгових залів. Витрати ресурсів на продаж однієї партії товарів кожного виду наведені в таблиці 10.4.
Таблиця 10А

Прибуток, одержаний від реалізації однієї партії товарів І виду, становить 500 тис. грн., 11 виду - 800 тис. грн., а 111 виду - 600тис. грн. Визначити оптимальну структуру товарообігу, яка забезпечить максимальний прибуток.
Для вирішення задачі потрібно: 1) побудувати математичну модель задачі; 2) знайти розв'язок задачі симплекс-методом; 3) дати економічну інтерпретацію отриманого оптимального плану.
Отже, побудуємо математичну модель цієї задачі:
Нехай хр х2, х3 - кількість партій продажу товару відповідно І, II та III видів; aZ- структура товарообігу, що забезпечує максимальний прибуток від реалізації (цільова функція). Звідси отримуємо систему нерівностей:
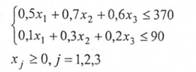
Крім того, цільова функція прагне до максимуму:
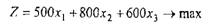
Для знаходження рішення системи нерівностей з врахуванням оптимальності цільової функції приведемо задачу лінійного програмування (ЗЛП) до канонічного вигляду таким чином, щоб вільні члени в обмеженнях (1.1) були додатними і система нерівностей замінилась системою еквівалентних рівнянь. Для цього додамо до лівої частини нерівностей додаткові невід'ємні змінні х4, х5. Отже, ЗЛП матиме такий вигляд:
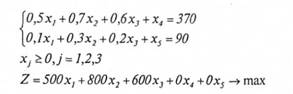
Далі побудуємо першу симплексну таблицю для цієї системи рівнянь, в яку запишемо її дані (табл. 10.5).
Таблиця 10.5
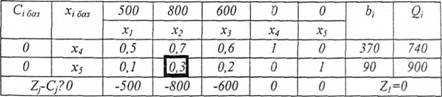
Охарактеризуємо умовні позначення, наведені в цій таблиці. У стовпчику С.баз містяться коефіцієнти цільової функції при базисних змінних, у стовпчику х.баз - позначення базисних змінних, у стовпчику ЬІ - вільні члени обмежень. Значення С^можна отримати додаванням порядкових добутків елементів стовпчика С1базі стовпчиках та відніманням коефіцієнта С^він записується в таблиці над позначенням "х." відповідної змінної).
Оберемо найбільшу за модулем від'ємну оцінку 2.-С. в нижньому рядку: це буде стовпчик х2 (-800). Цей стовпчик буде мати значення розв'язувального стовпчика. Знайдемо відношення елементів стовпця вільних членів Ь. до додатних елементів розв'язувального стовпця, запишемо результати в правий стовпчик йі і оберемо з них мінімальний Qimin(370/0,5; 90/0,1)=900. Отже, на перетині розв'язувальних стовпця і рядка знаходиться розв'язувальний елемент а =0,3.
Тепер визначимо елементи наступної таблиці за такими правилами. На місце елемента х, стовпця базисних змінних запишемо змінну х розв'язувального стовпця таблиці 10.1. В таблиці 10.2 на місце розв'язувального елемента запишемо одиницю. Всю решту елементів розв'язувального стовпця позамінюємо на 0. Всі інші елементи розв'язувального рядка поділимо на розв'язувальний елемент і запишемо на відповідні місця таблиці 10.6 нові числа (1/3; 2/3; 0; 10/3; 90/3).
Таблиця 10.6
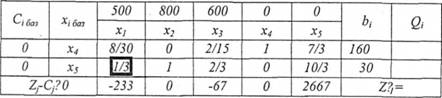
Стовпці, яким відповідають однакові базисні змінні таблиць 10.1 і 10.2 (в нашому випадку х^) залишаються незмінними. Незаповнені клітини перераховуються за правилом прямокутника: кожний елемент дорівнює поділеній на розв'язувальний елемент різниці добутку цього елемента на розв'язувальний елемент і добуток елементів, розташованих в основах перпендикулярів, проведених від цього елемента до розв'язувальних стовпчика і рядка. Таким чином, маємо для елемента, наприклад:
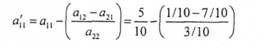
Поняття та галузь застосування
Концептуальний підхід
Загальні характеристики
Приклад застосування
Цілочисельне програмування
Поняття та галузь застосування
Приклад застосування
Література