Економічна теорія - Білецька Л.В. - Стійкість ринкової рівноваги. Концепція типу Л. Вальраса

Велику роль в розробці цих понять зіграв англійський економіст початку XX ст. А. Маршалл. Він розрізняє три типи рівноваги в залежності від наявності часу у виробників:

1. Миттєва рівновага, коли пропозиція незмінна. У фірми немає часу змінити пропозицію (рис. 8).

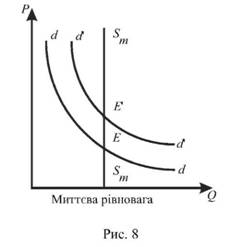
2. Короткострокова рівновага, коли фірми можуть більше виробляти продукції на існуючих підприємствах, пристосувавши працю і змінні фактори до умов, що змінилися (рис. 9).

3. Тривала рівновага, коли фірми можуть відмовитися від старих підприємств або збудувати нові, пристосувавши всі фактори та витрати до ціни, що змінилася. Тоді в даній галузі з’являються нові фірми, ряд інших фірм виходять з галузі (рис. 10).

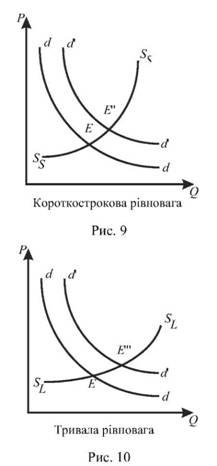
Зростання попиту здійснює різний вплив на ціну в різні періоди. У випадку миттєвої рівноваги збільшення попиту з аа до а’ а¹’ (наприклад, на товар, що швидко псується при незмінній пропозиції 5_т5_т) збільшує ціну з Е до Е’ при правильному розподілі пропозиції. У випадку короткострокової рівноваги пропозиція зростає, кількість підприємств не змінюється, крива попиту переміщується з аа до а’а’. Нова ціна рівноваги Е’’ нижча, ніж миттєва ціна Е’. У випадку тривалої рівноваги криві пропозиції 3₁Б₁ і попиту а’ а’ перетинаються в точці кінцевої рівноваги Е"’, яка досягається після того, коли всі економічні умови пристосувалися до нового рівня попиту. "Нормальна ціна" Е"’< Е"< Е’.

Стійкість ринкової рівноваги. Концепція типу Л. Вальраса

Ціна і обсяг товару (проданого і купленого) на ринку, який знаходиться в стані рівноваги, задані рівняннями попиту Б - а + аР і пропозиції 5 - Р + ЬР, де Р - ціна; а і а, Р і Ь - сталі; Б і

5 - лінійні функції. Рівноважні ціна Р і кількість товару 0 визначаються з умови Б - 5 :

Р _- а-Р о _- Ьа- аР

Ь - а а - Ь

Вивчення стійкості рівноваги передбачає включення динамічних процесів. Якщо в силу дії якихось факторів на ринку встановиться інша ціна, то чи буде наступний рух ціни у часі спрямований до стану рівноваги і наскільки швидко буде проходити процес пристосування? Початкове збурення (порушення рівноваги) може бути викликане використанням запасів товарів як продавцями, так і покупцями, існуванням запізнень з боку попиту і пропозиції. В дійсності може існувати декілька цін рівноваги. Велике початкове збурення може хитнути всю систему з одного стану рівноваги до іншого. Проблему стійкості розглядаємо при наявності невеликих початкових збурень.

Якщо ціна встановилася надто низькою, попит переважає пропозицію і ціна підвищується до тих пір, доки не буде досягнутий стан рівноваги. Так як відхилення ціни від її значення в умовах рівноваги Р - Р Ф 0, то величини попиту і пропозиції, що очікуються, не будуть рівними. Припустимо, що швидкість зростання ціни пропорційна швидкості зменшення запасів N:

^ІР --X - - -Х(5 - Б) - Х(а-Р)-Х(і - а)Р,

(її (Ії

де N(t) - запаси, що змінюються у часі; X - швидкість реакції, задана позитивна величина. Знак "-" означає різноспрямованість змін запасів і ціни. Чим більша X, тим швидша буде реакція ціни

на дефіцит пропозиції. Зробимо підстановку Р(() - Р для всіх ї:

0 - А,(а - Р) - Х(Ь - а)Р . Звідки Р - (а - Р)/(Ь - а), тобто знову прийшли до звичайної характеристики. Р рівномірно і монотонно прямує до Р , якщо (Ь - а) додатне і в такому випадку рівновага стійка. Р монотонно віддаляється від Р , якщо (Ь - а) від’ємне, і тоді рівновага нестійка.

Стійкість ринкової рівноваги. Концепція типу А. Маршалла

Вихідні умови такі ж, як і у випадку концепції типу Л. Вальраса.

Рівняння попиту Б - а + аР і пропозиції 5 = Р + ЬР - лінійні фу..... . . . _Р а Р . . .

нкції. У стані рівноваги ціна Р -- і кількість товару

Ь-а

7Т Ьа- аР _{Б с}

(2 -- визначаються з умови Б - 5 .

а-Ь

Вивчення стійкості рівноваги передбачає введення динамічних процесів. Якщо пропозиція надто мала, покупці запропонують більш високі ціни, ніж продавці готові були б прийняти, і пропозиція зросте до стійкої рівноваги. Обсяг пропозиції відрізняється від рівня, який забезпечує рівновагу, на величину д - 2 - 2 Ф 0 .

Побудуємо динамічну модель, в якій обсяг пропозиції збільшується, якщо ціни продавців нижчі тих, які пропонують покупці. Ціна покупця дорівнює Р_Б -(2 -а)/а, ціна продавця Р₅ -(2 - Р)) Ь. Швидкість збільшення обсягу пропозиції а2 / аї пропорційна розмірам дефіциту. Зміна обсягу пропозиції пропорційна зміні різниці - ціна продавця мінус ціна покупця. Тоді а2/аї - Х(Р/Ь-а/аЬ-1/аУ2, де X - швидкість реакції, величина позитивна, береться зі знаком "-", так як зміні обсягу пропозиції відповідає від’ємна різниця ціни продавця і ціни покупця.

2 монотонно прямує до 2 , якщо (і/Ь -1/а) додатне (стійка

рівновага), і 2 невпинно віддаляється від 2 , якщо (і/Ь -1/а) від’ємне (нестійка рівновага).

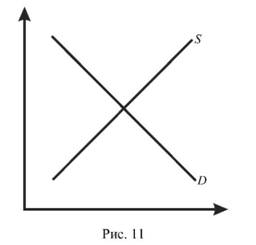
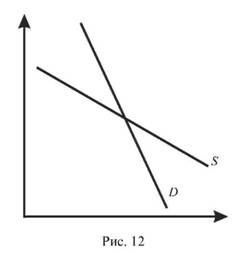
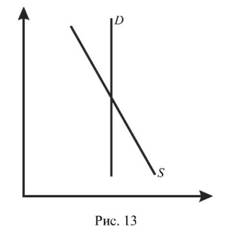
Стійкість у розумінні Л. Вальраса досягається при (Ь - а) > 0, в розумінні А. Маршалла - при (і/ Ь -1/ а)> 0. Різні результати отримані з таких причин. Крива попиту Б в усіх випадках спрямована вниз, кутовий коефіцієнт а < 0, а крива пропозиції 5 спрямована вгору, Ь > 0 (рис. 11), або спрямована вниз (Ь < 0), але з різним положенням відносно кривої попиту: на рис. 12 крива попиту крутіша за криву пропозиції (-Ь < -а); на рис. 13 крива пропозиції крутіша за криву попиту (-Ь > -а). Якщо крива пропозиції (11) спрямована вгору, Ь > 0, в даному випадку рівновага стійка і за Вальрасом і за Маршаллом; якщо крива пропозиції 5 (12) спрямована вниз, Ь < 0, а крива попиту Б крутіша за криву пропозиції

(-Ъ <-а), то рівновага стійка в моделі Вальраса і нестійка в моделі Маршалла; якщо крива пропозиції 5 (13) спрямована вниз, то в моделі Вальраса рівновага нестійка, в моделі Маршалла - стійка.