Економічна теорія - Білецька Л.В. - Крива В. Парето. Закон розподілу доходів

Австралійський економіст А. У. Філліпс у 1958 році довів, що між інфляцією та безробіттям існує зворотній зв’язок. При високому безробітті інфляція низька і навпаки. Цей взаємозв’язок у загальному вигляді він відобразив у кривих.

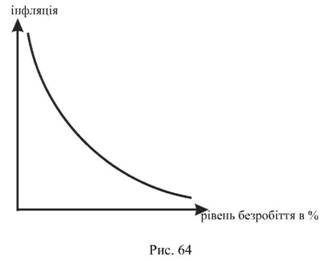
А. У. Філіпс з’ясував, що "у Великій Британії існує залежність між швидкістю зміни номінальної заробітної плати та частки безробітних у загальній чисельності робочої сили,... така залежність... залишалася стійкою на протязі 1861-1957 років":

_{щ =} ^^{( Л} ₌ ^ ^ ^

І ^ )

де ю - швидкість зміни ставок заробітної плати, сі і 5 - попит і пропозиція, и - частка безробітних у загальній чисельності робочої сили, / - форма функції.

Якщо врахувати зміни вартості життя (в процентах) і позначити його P, то залежність буде мати вигляд:

ю = f (u) + kP,

де k - позитивна постійна величина.

Якщо k = 1, то формулою виражається залежність між зміною реальної заробітної плати ю, вираженою в процентах, і часткою безробітних u . Якщо ж k < 1, це означає, що збільшення заробітної плати не повністю компенсує підвищення цін і реальна заробітна плата знижується.

Криві Е. Енгеля

На основі вивчення сімейних витрат (бюджетів) Енгель сформулював закономірність, названу його іменем: відношення частини доходів населення, призначеної для закупівлі продуктів, до загального доходу зменшується разом зі зростанням доходу.

На величину попиту на даний товар впливають різні фактори, але в першу чергу ціна P і дохід m . У першому наближенні попит d можна розглядати як функцію ціни та доходу: d = f (P, m).

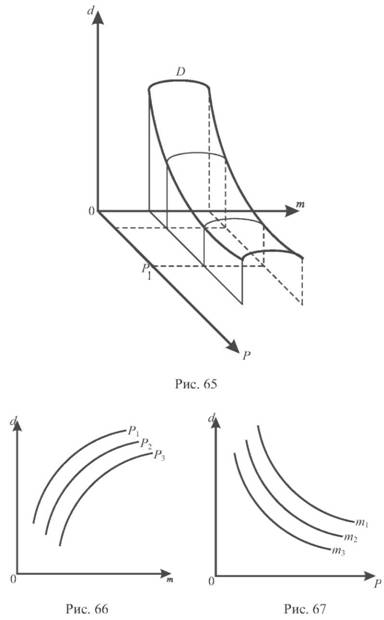
Попит можна представити графічно у трьох вимірах як деяку поверхню D (рис. 65). Припустимо, що ціна є постійною: P = P₁, тоді для цієї ціни попит d = f (P₁, m) і є функцією доходу m . На рис. 65 зображенням функцій, для яких P = const, будуть криві, які отримані шляхом перетину поверхні D площинами, перпендикулярними до осі OP, на якій відкладені величини ціни P. Це і є криві Енгеля.

На рис. 66 у двох вимірах представлені криві Енгеля для сталих P, P₂, P₃. Вони виражають залежність попиту від доходу за даної ціни.

Якщо ми припустимо, що дохід є постійним: m = m₁, то попит d = f (P, m₁) є функцією ціни. Зображенням таких функцій є криві, які утворюються шляхом перетину поверхні D площинами, перпендикулярними до осі Om .

На рис. 67 представлені криві, що виражають залежність попиту від ціни за допущення, що дохід є постійним, рівним відповідно m₁, m₂, m₃....

За допомогою кривих Енгеля, складених на основі сімейних бюджетів, можна кількісно оцінити вплив росту національного доходу на збільшення споживання.

Крива В. Парето. Закон розподілу доходів

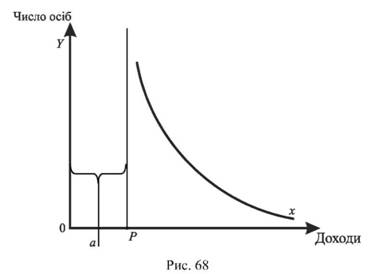
Використовуючи статистичні дані різних країн, В. Парето складав кумулятивні ряди розподілу особистих доходів, які показують оскільки осіб, які мають дохід не нижче вказаних у рядах величин. На осі абсцис відкладаємо величини доходів х, на осі ординат - число осіб, що мають дохід, рівний або більший х. Криві, які відображають такий розподіл доходу, є гіперболами, рівняння яких виражається формулою:

_ А

(х - а)

де а - мінімальний дохід, від якого на графіку починається крива, А і а - позитивні параметри.

Із рівняння виходить, що якщо х - 0, то у - 0 ; якщо у - °°, то х - 0 . Крива Парето має дві асимптоти: х = а та у = 0.

Якщо вісь ^У перенести в точку ^Р, яка відповідає мінімальному з розглянутих доходів, то а = 0 і рівняння кривої Парето має вигляд у = Ах^а або у = Ах~^а . На практиці зазвичай користуються цією спрощеною кривою В. Парето. Парето встановив, що величина параметра а кривої розподілу в різних країнах і в різні періоди коливається від 1,2 до 1,9, а в середньому а = 1,5 . Параметр а можна вважати деякою мірою нерівності в розподілі доходів. Чим більше а , тим більша увігнутість гіперболи, тим більший розрив між доходами окремих груп населення.

Крива характеризується такими властивостями: параметр а можна вважати показником еластичності чисельності осіб у відносно нижньої межі доходу х, еластичності зменшення кількості осіб при переході до більш високого класу доходів.

Перехід до більш високого класу доходів є легшим для осіб, які мають високий рівень доходів, ніж для тих, хто має низькі доходи. Математично це означає:

- = -аАх ~^а-1 - похідна функція розподілу доходу. Звідси відно-

Сх

сне зменшення числа осіб в міру зростання доходу складає:

Су - Аах"^а-1 , а , _---ах =--а .

у Ах ^а х

Пропорційне доходу зменшення відносного числа осіб при переході до все більших і більших доходів і складає сутність закону Парето. Для низьких доходів крива Парето не застосовується.

Існує багато соціологічних тлумачень закону Парето.