Концепції сучасного природознавства - Карпов Я. С. - 2.9.5.3 М. В. Остроградський

Михайлові Васильовичу Остроградскому (1801—1861) належать першокласні дослідження з методів інтегрування рівнянь аналітичної механіки й розробки узагальнених принципів статики й динаміки. Найбільш відомі дослідження Петроградського стосуються узагальнення основних принципів і методів механіки.

Він зробив істотний внесок у розвиток варіаційних принципів, які як окремий випадок включають і динаміку. Остроградський, розглядаючи варіаційну задачу, в якій підінтегральна функція залежить від довільної кількості невідомих функцій і їх похідних як завгодно високого порядку, доводить, що задача зводиться до інтегрування канонічних рівнянь Гамільтона, які можна розглядати як таку форму, в яку можна перетворити будь-які рівняння, що виникають у варіаційній задачі. Він також показав, що й у більш загальному випадку, коли зв'язки й силова функція містять час, рівняння руху також можуть бути перетворені у форму Гамільтона. Роботи Остроградського з механіки стали джерелом для подальших досліджень з метою з'ясування основ варіаційних принципів механіки.

У 1866 р. Остроградський висловив сумнів стосовно справедливості принципу найменшої дії Лагранжа. Основні заперечення Остроградського зводяться до того, що для Ейлера і Лагранжа принцип найменшої дії і найпростіша задача варіаційного числення являли собою одну й ту саму математичну проблему. Остроградський же зауважує, що в принципі найменшої дії змінні пов'язані законом живих сил і тому не є незалежними, на відміну від змінних звичайної варіаційної задачі. Звідси випливає також, що варіації змінних підпорядковуються певній умові й не можуть бути зовсім довільними. Тому Остроградський вважає формулювання принципу в Лагранжа і його висновки помилковими і дає власне формулювання: у випадку консервативної системи істинна траєкторія руху між двома точками має таку властивість, що перетворення рівнянь руху приводить до умови:

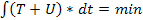
де U — потенційна функція,

Т — кінетична енергія системи.

І, навпаки, з мінімальності інтеграла можна одержати рівняння руху.

Принцип Остроградського, таким чином, відрізняється від принципу найменшої дії Лагранжа, в якому екстремуму досягає.

Питання про справедливість принципів Лагранжа й Гамільтон Остроградського викликало найжвавіше обговорення в математичній літературі. М. І. Тализін (1819-1869) і Ф. О. Слудський (1841-1891) показали, що обидва принципи — Лагранжа й Остроградського — однаково справедливі: "Вираження початку найменшої дії, які дали ці вчені, суть вираження двох різних загальних властивостей руху".

2.9.5.4 Немеханічне трактування принципу найменшої дії Гельмгольца

Перехід від власне механічної інтерпретації принципу Гамільтона до більш загального його розуміння, яке готувало грунт для некласичної концепції, відбувався в основному стихійно. Гельмгольц, який трактував принцип найменшої дії у виключно механічному розумінні, з 1886 р. систематично застосовував цей принцип до проблем механіки, термодинаміки й електродинаміки. Він увів поняття кінетичного потенціалу, що сприяло узагальненню фізичної інтерпретації принципу. Кінетичний потенціал — це величина, з якої можна одержати дію шляхом інтегрування за часом. Ця величина фігурувала в різних розділах фізики без якої-небудь механічної інтерпретації. У працях Гельмгольца кінетичний потенціал трактувався не як похідна величина — різниця між кінетичною і потенційною енергією, а як вихідна величина. Це було важливим кроком для переходу до немеханічного розуміння принципу найменшої дії, тому що кінетичний потенціал може відрізнятися від механічного поняття різниці T—U. Поза механікою, де розходження між кінетичною і потенційною енергією втрачає безпосередній смисл, кінетичний потенціал не можна одержати аналогічним способом, якщо енергія є заданою величиною. Тому самостійний характер поняття кінетичного потенціалу дозволяє зробити принцип найменшої дії універсальним принципом фізики зворотних процесів, не зводячи її закони до законів механіки; іншими словами, це дозволяє трактувати зазначений принцип уже не як механічний.