Психодіагностика - Галян І.М. - Застосування непараметричної і параметричної статистик при обробленні емпіричних даних

Непараметрична статистика як галузь математичної статистики дає змогу вивчати випадки, які передбачають нерівномірний або невідомий розподіл показників тестів.

Непараметричні методи статистики - методи математичної статистики, які застосовують за відсутності функціонального виду генеральних розподілів.

Використання їх розпочалося із запровадженням критеріїв знаків у ХVIII ст. У другій половині XIX ст. стали застосовувати ранги і коефіцієнти рангової кореляції. Рангові методи, які розробляв Ч.-Б. Спірмен, викликали інтерес у наукових колах. Унаслідок цього сформувалася непараметрична статистика як самостійна галузь математичної статистики.

У профвідборі використовують такі коефіцієнти: а) для шкали найменувань - коефіцієнт погодженості Пірсона х2' коефіцієнт контингенції Q, коефіцієнт асоціації Ф для чотирьохклітинної спряженості, К для М х N-клітинної спряженості, коефіцієнт взаємної спряженості Пірсона С і коефіцієнт взаємної спряженості Чупрова К;

б) для шкали порядків - коефіцієнт рангової кореляції Спірмена Rs , призначений для кореляції двох випадкових змінних, заснованих на рангових вимірюваннях і не діючих значеннях.

Розглядають особливості розрахунків деяких із названих коефіцієнтів, які найчастіше використовують при обробці тестів, у межах непараметричних методів математичної статистики.

Одними із найпростіших математично-статистичних обчислювальних мір є міри центральної тенденції, що дають змогу вираховувати середні значення.

Середнє (центральне) значення - узагальнювальний показний місця і рівня центру розподілу, тобто значення ознаки, навколо якої концентруються всі інші варіювальні значення.

Він є дуже важливим і поширеним параметром вибірки. Математична статистика трактує багато видів середніх величин. Кожна з них - це специфічна абстракція, яка має певний зміст, специфічне смислове навантаження, що робить середню величину "сплавом" кількісної і якісної оцінок. Тому вибір форми середнього значення - це вибір способу опосередковування даних, наявних у повному обсязі початкової вибірки. На всіх подальших висновках позначається таке опосередковування, оскільки воно відображає специфіку вибраної середньої величини і в цьому значенні є відносним. Проблема вибору адекватної середньої величини пов'язана з формою статистичного розподілу і відповідного її аналізу.

Отже, визначальним для кожного виду середньої величини є її якісний зміст - знання того, в якому значенні вона середня, в яких межах відбувається усереднення. В цьому контексті розглядають основні види середніх значень.

Основними мірами центральної тенденції є: мода, медіана, середнє арифметичне. Одні з них застосовують у непараметричній, а інші - у параметричній статистиці.

Мода (Мо) - величина, що найчастіше спостерігається у числовому ряду.

Вона вказує найтиповіше значення статистичної ознаки і становить особливий інтерес в асиметричному розподілі, де навколо значення моди концентруються найбільші частоти вибірки. Мода є середнім скупченням варіант, позначає місце і величину дії найсильнішого фактора серед тих, що формують статистичну сукупність, виявляють досліджувану ознаку. Мода становить клас найбільшої властивості, віднесеної до конкретних умов вимірювання.

Параметр моди незамінний для шкали найменувань, тобто у разі суто якісної градації варіант - конкретних значень оцінюваного параметра. Однак мода придатна і для всіх інших шкал вимірювання, особливо для випадків великої варіативності показника, для багатовершинних розподілів, де вона є своєрідним вираженням типу.

Емпіричне визначення (обчислення) параметра моди подібне до обчислення медіани, ґрунтується на формулі найпростішої інтерполяції:

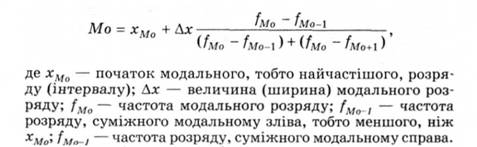
Крім емпіричного (тобто заснованого на результатах конкретного вимірювання) обчислення, існує також обчислення, засноване на теоретичному визначенні моди як точки, що відповідає максимуму кривої розподілу. При цьому до емпіричного розподілу підбирають одну з найбільш відповідних теоретичних кривих розподілу (наприклад, набір кривих Пірсона), а потім параметр моди обчислюють аналітично, тобто на основі відомої формули тієї чи іншої підібраної теоретичної кривої. Цей шлях обчислення є математично громіздким і використовується лише в спеціальних дослідницьких задачах.

Медіана (Ме, Мd) - середнє, центральне (за місцем) значення змінної в загальному впорядкованому ряді варіант вибірки.

Медіана є своєрідною серединою, справа і зліва від якої порівну розташовується решта варіант, тоді як їх питома вага, тобто абсолютна величина, не береться до уваги. Отже, Ме як середня, центральна величина є передусім якісною. Наприклад, для семи числових значень показника обсягу уваги (п = 7) (4, 6, 6, 8, 7, 6, 5) середнє арифметичне дорівнює 6. Для обчислення медіани (Мої) необхідно попередньо упорядкувати ряд числових значень показника від його мінімального значення до максимального, чи навпаки (для прикладу: 4, 5, 6, 6, 6, 7, 8 чи 8, 7, 6, 6, 6, 5, 4). Тоді медіану можна визначити як числове значення показника, що розташований в упорядкованому ряді даних посередині (медіана поділяє упорядкований ряд даних на дві однакові частини). За непарної кількості значень у ряду медіаною буде те числове значення показника, порядкове місце якого визначається виразом:

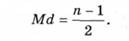
Коефіцієнт погодженості Пірсона х2 використовують для порівняння частот двох розподілів: двох емпіричних або емпіричного і теоретичного.

Коефіцієнт погодженості Пірсона х2 (Критерій х2 (хі-квадрат)) -

коефіцієнт, що ґрунтується на наближенні частоти прояву ознаки у різних вибірках, виміряної за номінативною шкалою.

Розрахунок здійснюють за формулою:

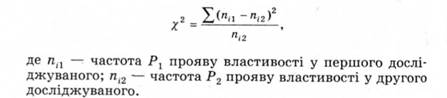
Застосування критерію вимагає, щоб обсяг розподілів, що зіставляються, мав не менше 20-30 варіант, а мінімальна їх частота - не менше п'яти (інакше слід укрупнити розряди).

Інші психологи (Б. Сосновський) пропонують таку формулу критерію х2'

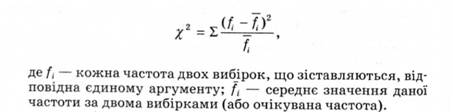
При зіставленні двох емпіричних вибірок обчислення спрощуються, якщо формулу £2 перетворити у такий спосіб:

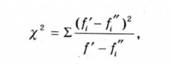
Алгоритм обчислення вказаного коефіцієнта можна з'ясувати на прикладі. При заучуванні двозначних чисел у двох групах досліджуваних при другому пред'явленні заучуваного ряду отримано результати, вміщені в табл. 2.5.

Таблиця 2.5. Результати заучування чисел

Слід з'ясувати, чи значущою є відмінність частот у цих двох групах. Кількість складених розрядів f = 5.

Обчислення Хі наведено в табл. 2.6 (за спрощеною формулою).

Таблиця 2.6. Обчислення коефіцієнта погодженості

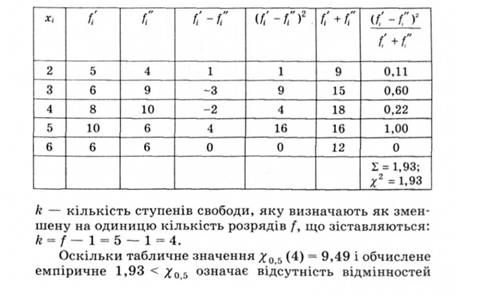
між частотами у двох групах досліджуваних, а обидві емпіричні сукупності можна вважати вибірками з однієї генеральної сукупності.

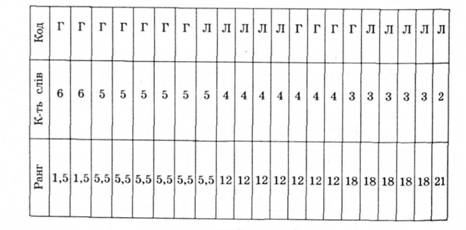
Для перевірки гіпотез використовують U-критерій Манна - Вітні. Розглянемо приклад його розрахунку. У процесі дослідження було отримано дані двох видів: одні - під час включення завдань у гру (Г), а інші - в процесі лабораторного експерименту (Л) (табл. 2.6).

Дані обох груп об'єднують у порядку зменшення числових значень, закодувавши належність даних до певної групи буквами "Л" (лабораторний експеримент) і "Г" (гра).

Кожному числовому значенню отриманого ряду надають ранг (порядковий номер). У разі збігу числових значень їм приписують середнє значення тих рангів, які були б подані кожному з них за відсутності збігу. Наприклад, дві 6 ділять між собою ранги 1 і 2, тому кожній з них нада-

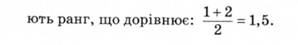
Таблиця 2.6. Таблиця значень для розрахунку коефіцієнта Манна - Вітні

Для перевірки обчислень використають вираз:

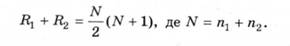
Підставляючи значення, отримують:

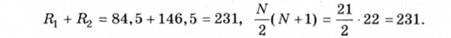
Отже, операції рангування і підсумовування рангів виконано правильно.

4. Обчислюють значення U-критерію за формулою:

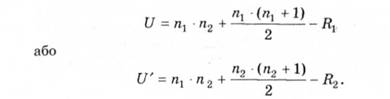
Підставляючи значення, отримують:

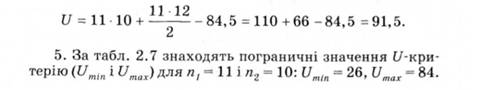
Таблиця 2.7. Пограничні значення U-критерію (рівень достовірності - 95%) (для Манна - Вітні)

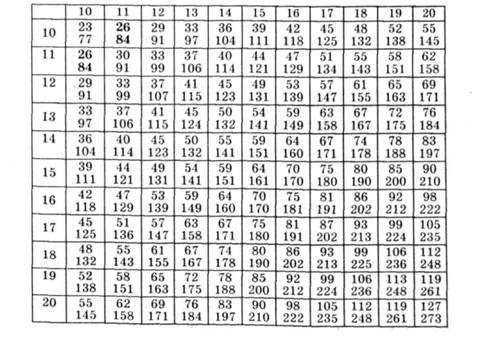
Отже, всі обчислення правильні.

У процесі оброблення результатів дослідження застосовують також переведення "сирих" балів у стени. Його можна виконати без створення стенової шкали, безпосередньо за загальною формулою:

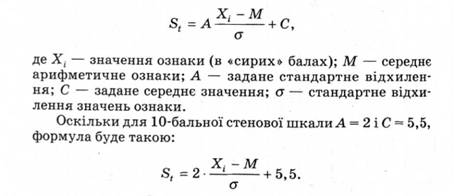
Для визначення статистичного зв'язку змінних, виміряних за дихотомічною шкалою найменувань, використовують коефіцієнт контингенції і коефіцієнт асоціації Ф.

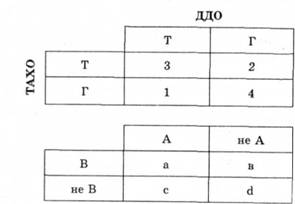
Для визначення алгоритму обчислення коефіцієнтів контенгенції та асоціації необхідно розрахувати статистичний зв'язок між технічною (Т) і гуманітарною (Г) спрямованістю школярів, виміряною дихотомічною шкалою найменувань за даними ТАХО (тест адекватних характеристик об'єкта) і ДДО (диференційно-діагностичний опитувальник).

Спочатку необхідно визначити кількість співвідношень технічної і гуманітарної спрямованостей за тестом ТАХО і ДДО (табл. 2.8).

Таблиця 2.8. Таблиця результатів дослідження спрямованості школярів (технічної та гуманітарної)

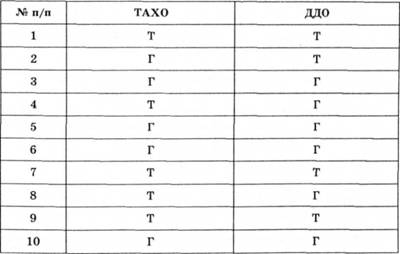
Результати слід занести до таблиці квадратів (табл. 2.9). Це необхідно для розрахунку залежності за формулами: а) для розрахунку коефіцієнта контингенції:

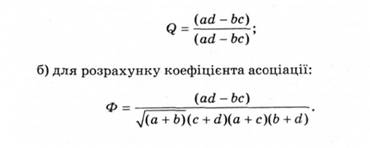
Таблиця 2.9. Таблиця квадратів для розрахунку коефіцієнтів контингенції та асоціації

Для вказаного прикладу це матиме такий результат: а) розрахунок коефіцієнта контингенції:

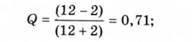
б) розрахунок коефіцієнта асоціації:

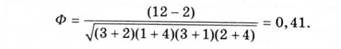
Отримані результати інтерпретують на основі співвідношення у такий спосіб: якщо теоретична Q і Ф більші ніж 0,5, це свідчить про сильний зв'язок; якщо теоретична Q і Ф менші ніж 0,5 - про слабкий зв'язок.

Для визначення статистичного зв'язку змінних, виміряних за порядковою шкалою, використовують коефіцієнт рангової кореляції.

ня за допомогою лінійної і нелінійної регресії (моделі регресії).

Параметричні методи статистики - методи математичної статистики, які застосовують у випадках, коли тестові показники виміряно за інтервальною шкалою, шкалою відношень або абсолютною шкалою при дотриманні розподілу Гаусса.

Особливості розрахунків деяких із названих коефіцієнтів розглянуто в межах параметричних методів математичної статистики.

Середнє арифметичне - величина, сума негативних і позитивних відхилень від якої дорівнює нулю. У статистиці його позначають буквою "М" або "X". Щоб підрахувати середнє арифметичне, потрібно додати всі значення ряду і розділити суму на кількість значень, які додавалися.

Середнє арифметичне (М) у найпростішому випадку обчислюється за формулою:

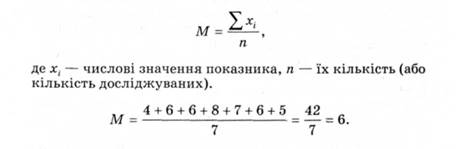
У процесі дослідження психолог може отримувати дані, розкидані в досить широкому діапазоні розкиду. Чим сильніше розкидані варіанти щодо середнього, тим більшим виявляється і середнє квадратичне відхилення.

Середнє квадратичне відхилення (а) - міра різноманітності об'єктів, що входять до групи, яка показує, наскільки в середньому відхиляється кожна варіанта від середнього арифметичного.

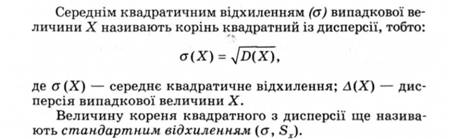
Обчислення дисперсії застосовують для виокремлення вибіркової сукупності, визначення помилки вибірки, однорідності досліджуваної сукупності за певною ознакою.

Дисперсія випадкової величини X - математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання.

її обчислюють за формулою:

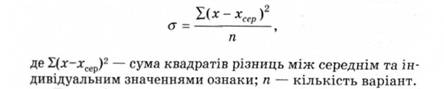
Дисперсією також називають варіації значення залежної змінної. Ті варіації, які можна пояснити дією незалежної змінної, називають первинною дисперсією; ті ж, що є результатом дії інших факторів, - вторинною дисперсією, або дисперсією помилки. Контролюючи рівень інших потенційних змінних, експериментатор прагне максимізувати долю первинної дисперсії.

Розкиданість значень характеризує і розмах W - різниця між найбільшим і найменшим значеннями в ряду:

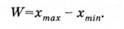
Розмах є найпростішою і приблизною мірою розкиданості значень, оскільки під час її обчислення використовують лише крайні елементи ряду.

Коефіцієнт варіації дає змогу порівняти в абсолютних одиницях варіативність вибірок незалежно від їх середнього значення.

Коефіцієнт варіації (V, СV) - виражене у відсотках відношення стандартного відхилення до середнього арифметичного значення.

Його обчислюють за формулою:

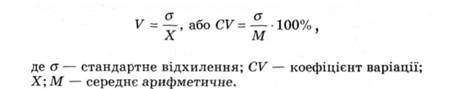
Сигма (σ) є величиною іменованою, тобто різною у різних одиницях вимірювання, і залежить не тільки від ступеня варіювання, а й від одиниць вимірювання. Тому за сигмою можна порівнювати мінливість лише одних і тих самих показників, а зіставляти сигми різних ознак за абсолютною величиною не можна. Щоб порівняти за рівнем мінливості ознаки будь-якої розмірності (виражені в різних одиницях вимірювання) і уникнути впливу масштабу вимірювань середнього арифметичного на величину сигми, застосовують коефіцієнт варіації- приведення даних до однакового масштабу величини о.

Для нормального розподілу існує точна кількісна залежність частот і значень, що дає змогу прогнозувати появу нових варіант: ліворуч і праворуч від середнього арифме-

ного розподілу, можна оцінити ступінь близькості до нього досліджуваного розподілу психологічної ознаки.

Кореляційні залежності можуть бути таких видів: 1) коефіцієнт кореляції Пірсона Rху що показує наявність статистичного зв'язку між змінними х і у, за якого кожній змінній х відповідає одне чи кілька визначених значень у, а розподіл у змінюється разом зі змінною х. Змінна може бути односпрямованою (+) і різноспрямованою (-). За певної кількості вимірів n-кореляційні зв'язки можуть бути значущими і незначущими. Це необхідно знати для достовірних висновків про причинно-наслідкові зв'язки змінних. Рівень значущості коефіцієнтів кореляції визначають за формулою розрахунку t-критерію за допомогою таблиць квантилей t-розподілу Стьюдента для довірчої ймовірності;

2) точково-бісеріальний коефіцієнт кореляції Пірсона Rpb, що є методом кореляційного аналізу відношення змінних. Змінні можуть вимірюватись за дихотомічною шкалою найменувань та за інтервальною шкалою відношень або порядку. Точково-бісеріальний коефіцієнт кореляції застосовують і для визначення дискримінативності завдань тестів.

Розрахунок кореляційних залежностей дає змогу здійснити факторний, кластерний і кореляційний аналіз емпіричних даних.

Факторний аналіз - розділ багатомірного статистичного аналізу, сутність якого полягає у виявленні безпосередньо невимірюваної ознаки, що є головним компонентом (похідною) групи вимірюваних тестових показників. Кластерним аналізом є сукупність статистичних і якісних методів, призначених для формування відносно віддалених одна від одної груп споріднених між собою об'єктів за інформацією про зв'язки (міри спорідненості) між ними. Факторний і кластерний аналіз практикуючі психологи використовують не часто.

Завдання психологічного дослідження полягає у з'ясуванні взаємозв'язків між двома або більше наборами даних. Однією з найпростіших форм виявлення такого зв'язку є кореляція. Саме кореляційний аналіз допомагає точно кількісно оцінити ступінь узгодженості змін (варіювання) двох і більше ознак.

Кореляційний аналіз - метод дослідження взаємозалежності ознак у генеральній сукупності, що є випадковими величинами і мають нормальний багатомірний розподіл.

Наочно інтеркореляційні показники подають як таблиці інтеркореляцій змінних, кореляційні матриці і графіки.

Ступінь узгодженості змін характеризує тіснота зв'язку - абсолютна величина коефіцієнта кореляції.

Наявність кореляції між двома результатами означає, що при зміні одного-результату інший також змінюється, тобто між результатами існує і виявляється зв'язок.

Якщо значення певної величини може змінюватися, її називають змінною. Кореляція між двома змінними може бути позитивною або негативною. Позитивною кореляцією вважають такий зв'язок між змінними, коли значення обох змінних збільшуються або зменшуються пропорційно: із зменшенням (збільшенням) однієї зменшується (збільшується) інша. Простим прикладом позитивної кореляції є зв'язок між зростом і вагою людини - із збільшенням зросту збільшується і вага. За негативної кореляційний зв'язок є обернено пропорційним: збільшення однієї змінної супроводжується зменшенням іншої (наприклад, температура повітря і кількість одягу: чим тепліше на вулиці, тим менше одягу вдягають).

Кореляція ще не означає наявності причинно-наслідкового зв'язку. Вона свідчить лише про наявність зв'язку, але не про те, що одна із змінних є причиною, а інша - наслідком. Існування причинно-наслідкового зв'язку встановлюють іншими методами.

Висновок про причинно-наслідкову залежність між явищами, що вивчаються, тільки на підставі статистичної значущості зв'язку між відповідними ознаками (на підставі коефіцієнта кореляції) робити не варто. Зазвичай статистичний зв'язок між ознаками - це необхідна, але не достатня умова причинно-наслідкового зв'язку між ними. Твердження про те, що явище А є причиною явища В, справедливе, якщо: одночасно явища А і В статистично пов'язані; А відбувається раніше В; відсутня альтернативна інтерпретація появи Б, крім А (іншими словами - відсутня загальна причина С сумісної мінливості А і В).

Застосування кореляційного методу дає змогу обґрунтувати наявність тільки статистичного зв'язку - однієї з трьох ознак причинно-наслідкового.

Наявність зв'язку між температурою повітря і одягом не означає, що якщо людина зніме одяг, то температура повітря підвищиться. Тому використано інші методи, щоб показати, що зв'язок є одностороннім, і причиною зміни кількості одягу є коливання температури повітря. В інших випадках зв'язок між двома змінними може бути обумовлений третьою змінною і кореляція просто відображає наявність чогось загального між двома змінними і третьою. Наприклад, якби .виникло бажання виміряти розмір ступні Школярів і оцінити їх знання з математики, то можна було б знайти позитивну кореляцію між довжиною ступні і глибиною знань з математики. Однак це не означає, що математичні здібності залежать від розміру ноги або що в тих, хто робить успіхи в математиці, швидше ростуть ноги. Кореляцію пояснюють впливом третьої змінної - віку (чим старша дитина, тим більша в неї нога, тим краще вона розуміє математику).

Після виявлення позитивної або негативної кореляції необхідно встановити, наскільки вона тісна. На це вказує коефіцієнт кореляції, який позначають буквою г. Величина г варіює в діапазоні від -1 до +1. У разі прямо пропорційної залежності однієї ознаки від іншої коефіцієнт кореляції дорівнює одиниці (тобто ознака корелює сама із собою). Негативний коефіцієнт кореляції свідчить про різну спрямованість варіювання ознак: при збільшенні одного інший зменшується, і навпаки.

Зазвичай виявляють кореляції з коефіцієнтами, що знаходяться в діапазоні між нулем (відсутність кореляції) і одиницею (ідеальна кореляція), і чим ближче значення r ±1, тим тіснішим є зв'язок. Значення г виражають в десяткових дробах (наприклад, -0,23; + 0,5). При низьких значеннях г (зазвичай низькими вважають значення, що не перевищують 0,2 при n < 30) кореляція, як правило, не є статистично значущою.

Нульова величина коефіцієнта кореляції свідчить про відсутність взаємозв'язку між ознаками, але це трапляється дуже рідко, бо у психічній сфері всі явища взаємопов'язані (переважно опосередковано, ці зв'язки можуть виявлятися лише на рівні тенденцій).

Враження, що значення г є безпосереднім показником сили кореляції, не є правильним. Наприклад можна дійти висновку, що, оскільки при ідеальній позитивній кореляції r = +1, то r = 0,7 відповідає 70% ідеальної кореляції (або r = 0,4 відповідає 40% ідеальної негативної кореляції). Насправді коефіцієнт кореляції є оманливим числом. Щоб знайти, яку відсоткову частку від ідеальної кореляції становить дане значення г, необхідно піднести його до квадрата, а результат помножити на 100. Якщо r = 0,7, то така кореляція становить 49% від ідеальної (0,7 0,7 o 100 = 49). Так само негативна кореляція г в - 0,4 становить 16% від ідеальної негативної кореляції. Тому "ступінь ідеальності" кореляції може бути набагато меншим, ніж видається, якщо зважати на значення г.

Фахівці статистики вважають, що коефіцієнт кореляції вказує на частку змін однієї змінної, які можна передбачити за змінами іншої. Існує багато методів вимірювання кореляції, і вибір конкретного методу залежить від типу даних.

Алгоритм обчислення коефіцієнта кореляції Пірсона (r) є мірою кореляції між двома змінними, розподіленими за нормальним законом (наприклад, для виявлення взаємозв'язку рівня розвитку інтелекту й адаптивних можливостей особистості) (рис. 2.10). Перевага цього методу полягає в тому, що на величину кореляції не впливає те, в яких одиницях вимірювання представлені ознаки. Недоліком методу є складність математичних обчислень, особливо для великих масивів даних. Його усувають застосуванням прикладних програм (наприклад, Excel).

Таблиця 2.10. Таблиця розрахунку коефіцієнта кореляції Пірсона на прикладі реальних емпіричних даних

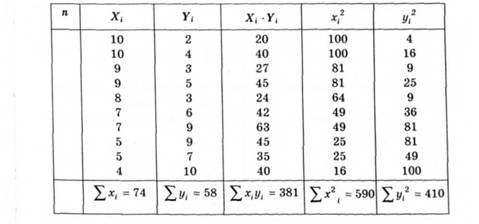
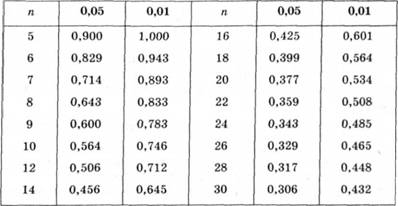
Отримані з обчислень дані перевіряють на значущість за таблицею критичних значень (табл. 2.11).

За неможливості дотримання цих вимог, а змінні є обчисленими за порядковою шкалою (чи переведені за нею), доцільніше використовувати (особливо за малого обсягу даних) як міру зв'язку непараметричну статистику.

Таблиця 2.11. Критичні значення rху (для рівнів значущості 0,05 і 0,01)

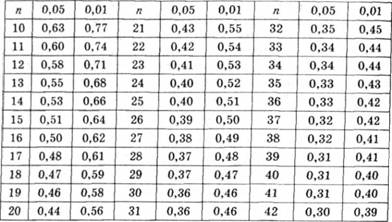
Непараметричним еквівалентом цієї оцінки є коефіцієнт кореляції Снірмена (р) (наприклад, для порівняння порядку приходу до фінішу одних і тих самих бігунів у двох забігах або виявлення зв'язку між успішністю з математики і часом розв'язання арифметичної задачі), що вираховують за формулою:

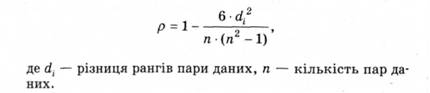
Обчислення значень для цієї формули представлено у табл. 2.12.

Таблиця 2.12. Алгоритм розрахунку значень коефіцієнта кореляції Спірмена (р)

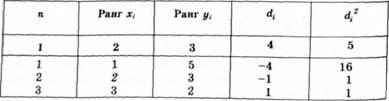
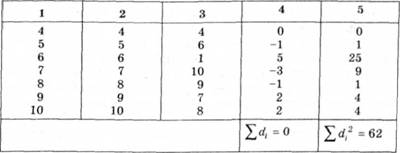
Критичні значення r (для рівнів значущості 0,05 і 0,01)

Перевага цього методу полягає в можливості здійснення нескладних математичних обчислень з використанням калькулятора для невеликих за обсягом вибірок. Недоліком методу є обмеження, що спричинені складністю оброблення значних масивів даних і необхідністю рангування рядів значень.

Варіантом кореляції е також зв'язок, який описує рівняння регресії (параметрична оцінка). Виявляючи кореляцію, дослідник зацікавлений продемонструвати наявність зв'язку між двома змінними. При визначенні рівняння регресії робиться спроба не тільки продемонструвати наявність зв'язку, а й передбачити фактичне значення однієї змінної за значенням іншої. Наприклад, визначивши рівняння регресії, що пов'язує зріст і вагу, професійні установки і ефективність професійної діяльності, можна не тільки продемонструвати, що вони пов'язані, а й отримати формулу для прогнозування зросту людини за її вагою, чи навпаки, або рівня ефективності майбутньої діяльності. За допомогою традиційного рівняння регресії аналізують зв'язок між двома змінними. При застосуванні багатовимірного рівняння регресії можна прогнозувати значення однієї змінної за значенням двох або кількох інших. У багатьох випадках його використання забезпечує точні результати. Наприклад, можна застосувати традиційне рівняння регресії для прогнозування загальних академічних досягнень за наслідками тестування математичних здібностей. З використанням багатовимірного рівняння регресії можна скласти той самий прогноз на основі оцінок не тільки з математики, а й з англійської мови чи природничих наук. Багатовимірне рівняння регресії забезпечить точніший прогноз. Проте метод вимагає використання спеціальних прикладних програм математичної статистики.

Межі довірчого інтервалу середнього арифметичного.

Статистичні методи застосовують у визначеному довірчому інтервалі, який задають відповідно до потреб точності вимірів.

Довірчий інтервал пов'язаний з інтервальним оцінюванням. Інтервальна оцінка параметра (у т. ч. середнього арифметичного) - це інтервал числової осі, в межах якого лежить значення параметра. У цьому разі замість одного числа (точкової оцінки) вказують нижню і верхню межі інтервалу, тобто групу суміжних точок на числовій осі, одна з яких, імовірно, і є значенням параметра. Коли інтервал будують з урахуванням вірогідності потрапляння значення параметра в межі інтервалу, його називають довірчим інтервалом. Довірчий інтервал виражається за допомогою довірчого коефіцієнта. Він вказує, що будь-який статистичний висновок є висновком імовірнісним - таким, що містить ризик допустити помилку (наприклад, з незначною вірогідністю - 0,05, або 5%).

Прикладом побудови 95-відсоткових довірчих інтервалів для середнього арифметичного і медіани є дані про швидкість читання першокласників. 16 випадково вибраних учнів першого класу було обстежено наприкінці навчального року з метою визначення середньої швидкості читання (показник - кількість слів за хвилину для тексту певної складності); при цьому були отримані такі числові значення показника: 30, 40, 40, 45, 45, 45, 50, 50, 50, 50, 55, 55, 60, 60, 60, 65.

Отриманий ряд даних характеризується середнім арифметичним М = 50 і стандартним відхиленням а =9. При аналізі цих величин у вчителя-дослідника зазвичай виникають стандартні питання для всіх подібних ситуацій: чи можна очікувати, що при повторенні подібних дослідів у тих самих умовах і з тим самим матеріалом, але на інших вибірках будуть отримані подібні результати; яких висновків можна дійти про певні якості особистості, спираючись тільки на отримані дані і не проводячи ніяких додаткових дослідів. Ця група питань пов'язана з проблемою надійності статистичних характеристик, розрахованих за вибірковими даними.

Для з'ясування надійності можна скористатися експрес-методами оцінювання меж довірчих інтервалів (табл. 2.14).

Таблиця 2.14. Значення коефіцієнта kn для розрахунку меж довірчих інтервалів середніх арифметичних (рівень достовірності - 95%)

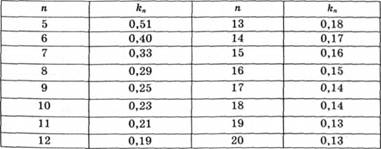
Верхню і нижню межі довірчого інтервалу середнього арифметичного можна визначити за формулами:

Таблиця 2.15. Порядкові номери числових значень у впорядкованому за збільшенням ряді даних, які можуть бути прийняті як нижня і верхня межі довірчого інтервалу медіани (рівень достовірності - 95%)

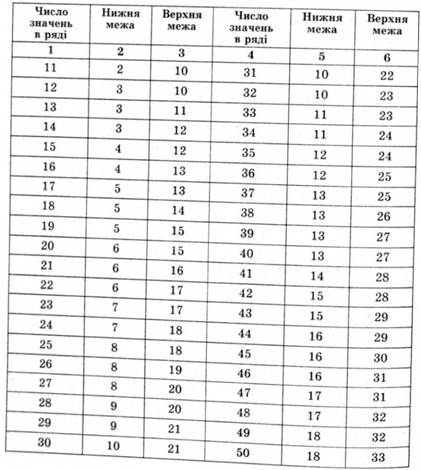
Ще простіше оцінюють межі довірчого інтервалу медіани. Для цього на впорядкованій сукупності числових значень швидкості читання 30, 40, 40, 45, 45, 45, 50, 50, 50, 50, 55, 55,60,60, 60, 65 достатньо за табл. 2.15 знайти номери значень, які можуть бути прийняті на цьому рівні достовірності як нижня і верхня межі довірчого інтервалу Md (у прикладі точкова оцінка медіани дорівнює 50). За табл. 2.15 значення 4 і 13 у ряду даних (подані жирним шрифтом).

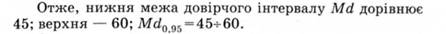
Отримавши інтервальну оцінку середнього або медіани, що відображає і розкиданість числових значень показника і їх кількість, можна зробити попередні діагностичні висновки.

Так, швидкість читання від 45 до 55 слів за хвилину (інтервальна оцінка М) можна взяти за середню швидкість читання першокласників наприкінці навчання, тоді швидкість читання менше 45 слів за хвилину можна вважати нижчою за середню, а швидкість більше 55 слів за хвилину - вищою за середню (приклад умовний). Аналогічні висновки можна робити, спираючись на інтервальну оцінку Мd. Однак для чітких діагностичних висновків застосовують складніші статистичні методи побудови норм, що розраховують на основі великої сукупності даних.

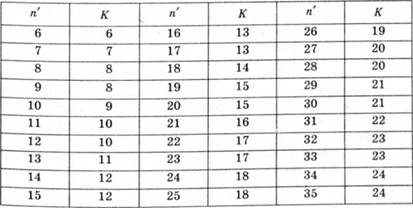
Таблиця 2.16. Пограничні значення критерію знаків (рівень достовірності - 95% )

Для оцінювання подібності двох груп досліджуваних, у яких виміряні певні властивості за середньою і дисперсією тестових даних, застосовують f- критерій Фішера, t- критерій Стьюдента, x- критерій Велша. t- критерій застосовується в ситуації рівності СКВ. t- критерій визначає подібність вибірок за дисперсією їх емпіричних змінних. Дослідники найчастіше послуговуються г-критерієм Стьюдента.