Математична статистика - Руденко В.М. - 2.3. КОРЕЛЯЦІЙНИЙ АНАЛІЗ

Завданням описової статистики є не лише систематизація емпіричних даних у вигляді розподілу частот та розрахунки типових показників МЦТ і варіацій ознак ММ, а й виявлення зв'язку між змінними, оцінювання його напряму та інтенсивності. Порівнюючи різні види зв'язків, можна виділити три типи залежностей між змінними X і Y:

функціональна залежність визначає значення змінної Y від X однозначно;

кореляційна залежність визначає середнє значення змінної Y від X;

стохастична залежність визначає розподіл змінної Y від X.

Отже, найбільш загальною вважається стохастична залежність. Кореляційна залежність є залежністю стохастичною, функціональна - розглядається як окремий випадок кореляційної залежності.

Сутність кореляції

Кореляція (від лат. correlatio - співвідношення) - це статистична залежність між випадковими величинами, що носить імовірнісний характер.

Кореляційні зв'язки можна вивчати на якісному рівні з діаграм розсіяння емпіричних значень змінних X і Y (рис. 2.51) і відповідним чином їх інтерпретувати. Так, наприклад, якщо підвищення рівня однієї змінною супроводжується підвищенням рівня іншої, то йдеться про позитивну кореляцію або прямий зв'язок (рис. 2.51 а, б). Якщо ж зростання однієї змінної супроводжується зниженням значень іншої, то маємо справу з негативною кореляцією або зворотним зв'язком (рис. 2.51 г, ґ). Нульовою називається кореляція за відсутності зв'язку змінних (рис. 2.51 в). Проте нульова загальна кореляція може свідчити лише про відсутність лінійної залежності, а не взагалі про відсутність будь якого статистичного зв'язку .

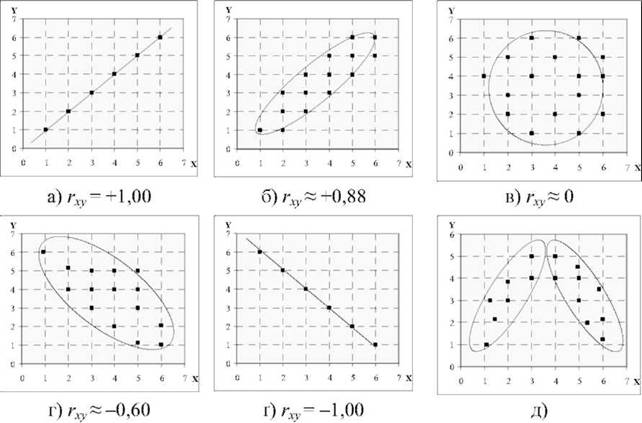
Рис. 2.51. Діаграми розсіяння емпіричних значень змінних Xі У:

а) строга позитивна кореляція; б) сильна позитивна кореляція; в) нульова кореляція; г) помірна негативна кореляція; ґ) строга негативна кореляція; д) нелінійна кореляція

У психолого-педагогічних дослідженнях здебільшого спостерігаються зв'язки нелінійні (див. рис. 2.51 д). Наприклад, зростання мотивації спочатку підвищує ефективність навчення, а потім наступає зниження продуктивності (ефект "перемотивації" - закон Иеркса-Додсона). Кількісна міра кореляційного зв'язку оцінюється за значеннями коефіцієнтами кореляції у межах від -1 до +1. Від'ємні значення коефіцієнтів указують на зворотний зв'язок, додатні - на прямий. Нульове значення може свідчити про відсутність зв'язку. Інтенсивність зв'язку (слабкий зв'язок - помірний - суттєвий - сильний) оцінюється за абсолютним значенням коефіцієнтів кореляції.

Методи розрахунку міри кореляційних зв'язків тісно пов'язані із вживаними вимірювальними шкалами (табл. 2.4) .

Таблиця 2.4

Коефіцієнти кореляції залежно від типів вимірювальних шкал

Вивчення зв'язку між ознаками, які приймають випадкові значення, починається з оцінювання його лінійності.

Лінійна кореляція

Лінійний кореляційний зв'язок для емпіричних даних, виміряних за шкалою інтервалів або відношень, оцінюється за допомогою коефіцієнта кореляції Пірсона г_ху

де Хі і у і - значення змінних X і У; х і у - середні X і У; п - обсяг вибірки.

⁸ Зазначені методи розрахунку з використанням комп'ютерної техніки можна знайти у підручнику [56].

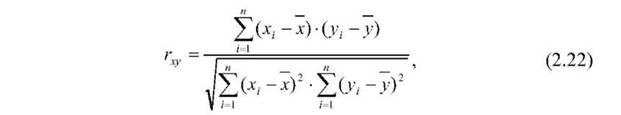
Формула (2.22) може бути перетворена, якщо замінити значення змінних Хі і у і нормованими значеннями 2_х і г_у, і виглядатиме так:

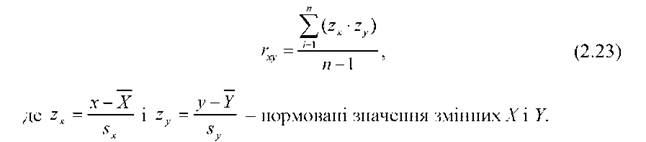
Приклад 2.7. Оцінити зв'язок між змінними X і У за емпіричними даними таблиці рис. 2.52 двома способами з використанням формул (2.22) і (2.23). Спосіб 1.

Послідовність рішення:

o оцінити характер лінійності зв'язку між ознаками X і У за допомогою діаграми розсіяння (рис. 2.52);

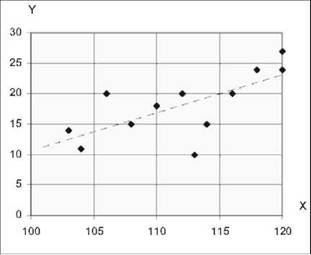
Рис. 2.52. Діаграма розсіяння ознак

o переконатися, що кореляція лінійна, і продовжити розрахунки коефіцієнта кореляції Пірсона г_ху (рис. 2.53 і 2.54);

o у комірках В16 і С16 розрахувати середні значення х і у

х = і х_і = 112,00; У = ¹ ул = 18,17;

o у комірках і в15 розрахувати суми квадратів різниць:

X (х, - X)² = 386,00; £ (у, - у)² = 311,67;

¡=1 ,=1

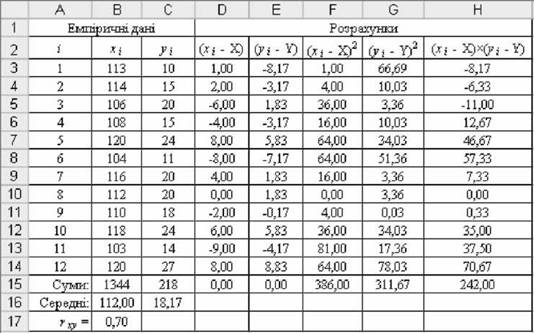
Рис. 2.53. Результати розрахунку коефіцієнта кореляції г_ху

o у комірці Н18 розрахувати суму добутків різниць:

X (х_і - X) o (у_і - у) = 242,00;

¿=1

o у комірці В17 розрахувати коефіцієнт кореляції г_ху за формулою:

гху =■ ^242,00 - 0,70. л/386,00 o 311,67

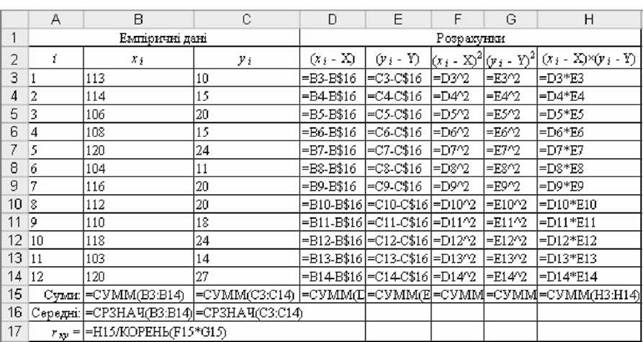
Рис. 2.54. Розрахункові формули Значення г_ху ~ +0,70 свідчить про суттєвий прямий зв'язок між ознаками.

Спосіб 2.

Послідовність рішення:

o Результати розрахунку г_ху за нормованими даними показано на рис. 2.55, розрахункові формули рис. 2.56.

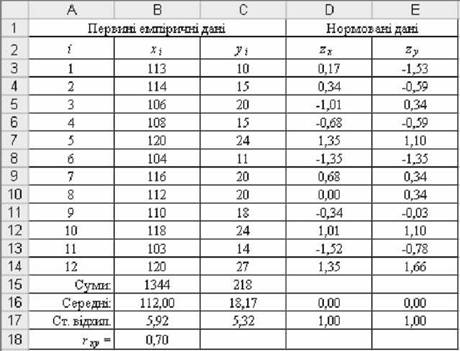
Рис. 2.55. Результати розрахунку г_ху за нормованими даними

o у комірках В16 і С16 розрахувати середні значення х і у;

o у комірках В17 і С17 розрахувати стандартні відхилення у_х і у_у;

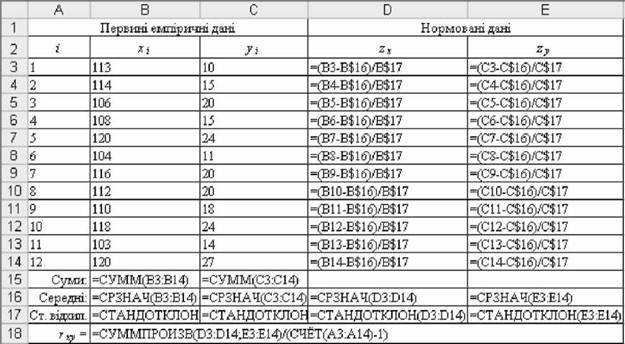
Рис. 2.56. Формули розрахунку г_ху за нормованими даними o у стовпчиках Б і Е розрахувати нормовані дані 2_х і 2_у (зверніть увагу,

що середнє нормованих даних дорівнює 0, а стандартне відхилення - 1,00);

o у комірці В18 розрахувати коефіцієнт кореляції r_xy за формулою (2.23);

Висновки. Одне те саме значення r_xy ~ +0,70 розраховано двома способами. Методи розрахунку за нормованими даними виглядають більш лаконічно. Значення парного коефіцієнта кореляції Пірсона r_xy можна також отримати за допомогою спеціальної функції MS Excel =ПИРСОН().