Теорія статистики - Мармоза А.Т. - Інші види середніх величин

Крім розглянутих вище видів середніх величин, статистикою розроблено і інші види.

Середня хронологічна являє собою середню величину з показників, що змінюються у часі. Вона розраховується із рівнів моментного або інтервального рядів динаміки за принципом середньої арифметичної простої і зваженої.

Для інтервального ряду динаміки середня хронологічна проста

обчислюється за формулою у = -2^-, п

де у - рівень ряду динаміки, п - число рівнів у ряду динаміки.

Для моментного ряду динаміки (при рівній відстані періодів, наприклад, місяць, квартал і т.д.) середня хронологічна проста обчислюється за формулою:

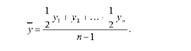
Середня хронологічна зважена має вигляд у = ^-, якщо відомий час,

протягом якого зберігалось кожне значення у. Тут і - період часу, який відокремлює один рівень від іншого.

Для виявлення тенденції зміни досліджуваного явища у часі розраховують середню ковзну. Суть способу її розрахунку полягає в тому, що склад періоду безперервно і постійно змінюється - відбувається зсув на одну дату при збереженні постійного інтервалу (триріччя, п'ятиріччя І т.д.).

Приклади і методика розрахунку середньої хронологічної і середньої ковзної наведені при розгляді рядів динаміки (див. розділ 10).

В аналізі і плануванні застосовується також середня прогресивна. Цей вид середньої на відміну від загальної середньої дає узагальнену характеристику не всієї сукупності, а тільки тієї її частини, яка представлена показниками вищими за загальну середню.

Середню прогресивну обчислюють у такій послідовності: 1) з усіх варіант обчислюють загальну середню; 2) відбираються варіанти, що за величиною перевищують загальну середню; 3) по відібраних варіантах обчислюють середню.

Вона й буде середньою прогресивною. Наприклад, якщо сукупність представлена

рядом чисел Xl,X2,ooo,Х8 та їх середнім значенням х, серед яких xl,х2 і Х8 виявляться більшими за розміром чим загальна середня, то середня прогресивна становитиме:

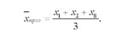
Особливим видом середніх величин є середня багатовимірна, яка являє собою середню величину кількох ознак для однієї одиниці сукупності. Оскільки неможливо розрахувати середню величину за абсолютними значеннями різних ознак (різноякісних, виражених у різних одиницях виміру), то багатовимірна середня визначається з відносних величин (часток, процентів і т.п.), як правило, з відношень абсолютних значень для одиниці сукупності до середніх значень цих ознак.

Середня багатовимірна - похідна величина, розраховується для статистичної сукупності чисельністю N одиниць з порядковими номерами і (і = 1, 2, 3,...Д ), які володіють к ознаками (х) з порядковими номерами і (і =1, 2, 3,...,к), таким чином. Спочатку обчислюють відношення Рц значень кожної ознаки (х) у кожної х величини сукупності до її середнього значення за формулою Р = -, де хіц - хі значення і'-ої ознаки у і-ої одиниці сукупності; хц - її середнє значення. Після цього визначають середню з цих відношень для кожної одиниці сукупності (рі), яку і називають багатовимірною середньою:

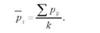
Багатовимірні середні дають узагальнену характеристику кожної одиниці сукупності за кількома ознаками одночасно. При цьому значущість ознаки для багатовимірної оцінки одиниці сукупності вважається однаковою, що економічно, звісно, неточно.

Розрахунок середньої багатовимірної розглянемо на прикладі порівняльної оцінки якості ґрунтів по групі господарств (табл. 4.6).

Таблиця 4.6. Дані для розрахунку середньої багатовимірної

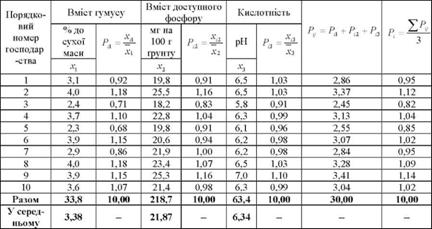
Poзpaxoвaнi бaгaтoвимipнi cepeднi дають змогу здійснити пopiвняльнy оцінку якості ґрунтів по гpyпi гocпoдapcтв за тpьoмa найважливішими їхніми ознаками. З даних таблиці видно, що кращі грунти мають дев'яте і друге господарства, а гірші - третє і п'яте господарства.

Середню багатовимірну використовують для аналізу господарської діяльності підприємств, зокрема при визначенні ефективності використання виробничого потенціалу (землі, трудових ресурсів, виробничих фондів) та ін.