Страхування на дожиття строком на п років передбачає виплату після закінчення п років лише тоді, коли застрахований буде живий після п років з моменту укладення страхової угоди. Якщо сума, що буде виплачена, становить 1, то
' г0,г^д, (0,Т<п,
' [1,г>ті, 1 |ил,Г>л.
Єдиним елементом невизначеності у страхуванні на дожиття є факт того, відбудеться чи не відбудеться страхова виплата. Розмір і час здійснення виплати за умови, що виплата відбудеться, визначені заздалегідь. У виразі Z = u*Y величина У є індикатором події "дожиття до віку х + я". Ця величина набуває значення 1, якщо застрахований доживе до віку х + п, і значення 0 у протилежному випадку. Для позначення актуарної поточної вартості страхування на дожиття строком на п років є два символи. У контексті страхування це величина Ах~.1. У наступному підрозділі ми побачимо, що в контексті ануїтетів ця величина позначається через ЛЕХ.
Д[2]=о"і>т=и""рх пдг =2 АЛ -(А^У- (25.6) Змішане страхування строком на п років передбачає виплату після смерті страхувальника або після дожиття до д-річ-ного віку залежно від того, що сталося раніше. Якщо розмір виплати - 1 і виплати на випадок смерті здійснюються в момент смерті, то
ь,=і,г£0, о, = я г= п
[ип,г>7і, [и",Т>п. Актуарна поточна вартість позначається через Ах-. Окрім того,
ОД=2ЛжвГажВІ)2. (25.7)
Таке страхування можна розглядати як комбінацію страхування на випадок смерті строком на п років і страхування на дожиття строком на п років - у кожному випадку з виплатою розміром 1. Нехай 2,, 22 і 23 - випадкові величини, що позначають поточну вартість угоди строкового страхування, страхування на дожиття і змішаного страхування відповідно, в кожному з яких страхова виплата здійснюється в момент смерті особи (х). Тоді з попередніх визначень:
_Іог,Г<и, ГО.Т^л, _Гит,Т£л,
1~[0,Т>п, 2~[оп,Т>п, 8 [оТ>д. Очевидно, що
Яз^+Я,, (25.8)
і порахувавши математичне сподівання обох частих, отримаємо
За допомогою рівняння (25.8) знайдемо 2)[£3]:
2)[^8]=2>[^1]+2)[^2]+2Соу(^і" (25.10)
Оскільки соо(г19 г2)=м[г1 г2]-м[г1]Е[г2]
і Zl Zг = 0 для всіх Т, то
сои(гг, г^-оддаг.]--^ - (б.іі)
Підстановка формул (25.4), (25.6) і (25.11) у (25.10) дає формулу для D[Z3] у термінах актуарної поточної вартості для страхування на випадок смерті строком на п років і для страхування на дожиття.
Відстрочене страхування
Страхування, відстрочене на т років, передбачає виплату відразу після смерті страхувальника лише в тому випадку, якщо він помре не раніше ніж через т років після укладення страхової угоди. Сума, що виплачується, і строк, на який укладено угоду, можуть бути будь-якими зі згаданих вище. Наприклад, безстрокове страхування на випадок смерті, відстрочене на т років, з виплатою на час смерті страхувальника суми, що дорівнює 1, визначається співвідношенням
' [0,"<т, 1 {0,Тйт.
Актуарна поточна вартість такого страхування позначаєть-
ся через т1Ах і дорівнює МАХ = ]и' * Ірх -их(г)<&
т
Приклад 25.3. Розглянемо безстрокове страхування на випадок смерті, відстрочене на чотири роки, з виплатою в момент смерті особи (х). Інтенсивність смерті ц для цієї особи дорівнює 0,05. При 6 = 0,10 для розподілу поточної вартості виплат підрахуємо математичне сподівання та дисперсію.
Для будь-яких ц і 6
41 * і ^ ц + 6 Тому для ц = 0,05і6 = 0,10
Лхж!*** =0,1836, Я[2] =-^-е^о.о5+о.2о>_ 1 -,.2 =0 04
1 3 0,05+0,20 9
Страхування зі змінними виплатами
Загальну модель, що визначається формулою (25.1), можна використати в більшості застосувань. Ми використали її стосовно угод страхування життя з постійними виплатами. Також вона може застосовуватись до угод страхування, в яких величина виплат на випадок смерті або зростає, або спадає в арифметичній прогресії протягом усього строку дії страхової угоди або частини цього строку. Цей страховий продукт часто пропонується як додаткове покриття, коли основна страхова угода забезпечує повернення премій, що періодично сплачуються, в момент смерті, або коли ануїтет містить гарантію того, що виплати будуть відповідати обумовленій у цій угоді початковій премії.
Безстрокове страхування на випадок смерті з щорічно зростаючими страховими виплатами, відповідно до яких сплачується 1 у момент смерті протягом першого року, 2 в момент смерті протягом другого року і т. ін., характеризується такими функціями:
Ь|-[" + 1], *£0, о(=и'( і£0, 2=[Т + 1]от, Т£0, де [а] позначає цілу частину числа а.
Актуарна поточна вартість для такого страхування позна-
чається через (ІА)Х і дорівнює М[2]= |[г+1]и' o ,рх|ія(г)Л
о
Збільшення страхової виплати, зазначеної в страховому договорі, можуть відбуватися частіше або рідше ніж один раз на рік. Для безстрокового страхування на випадок смерті зі страховими виплатами, що зростають т разів на рік, випла-1
ти становлять - у момент смерті протягом першого з т штер-
т о
валів, на які буде поділений рік, - в момент смерті протягом
т 1
другого такого інтервалу і т. ін., збільшуючись на - в кожно-
т
му наступному інтервалі. Для такого страхування життя
т т
Актуарна поточна вартість - це
(Ґт)А)х = М[2Г.
Граничний випадок при т -> со для безстрокового страхування на випадок смерті зі страховими виплатами, що зростають т разів на рік, є страхуванням з виплатою суми £ в момент смерті і. Відповідні функції мають вигляд Ь( =г, і>0, о, =іУ, г^0, 2 = То7', Г>0.
У цьому випадку актуарна поточна вартість позначається через (ІА)Х. Таке безстрокове страхування на випадок смерті з неперервним збільшенням розміру виплат еквівалентне множині угод безстрокового відстроченого страхування на випа-
док смерті з постійними виплатами1. З цієї еквівалентності випливає, що актуарні поточні вартості для зазначених страхувань однакові. Тобто
ас ао
(ТА), = /*о' o ,р,цж(*)<" = І4А.аі1-
0 0
Якщо за будь-якою з таких угод зі збільшенням розмірів виплат т разів на рік виплата на випадок смерті відбудеться лише у випадку, якщо смерть настала не пізніше ніж через п років з моменту укладення угоди, то ця угода називається угодою страхування на випадок смерті строком на п років зі страховими виплатами, що зростають т разів на рік.
У певному сенсі протилежними до угод страхування на випадок смерті строком на п років з щорічно зростаючими виплатами є угоди страхування на випадок смерті строком на п років з щорічно спадаючими страховими виплатами, згідно з якими в момент смерті, що сталася у першому році, виплачується сума п, у момент смерті, що сталася у другому році, - сума п-1 і т. д., так, що виплата стає нульовою по закінченні п-го року. Такій угоді відповідають функції
о. =< Л и, = о , г > 0, £ = <
' [ 0,і>п, 1 0,Т>п.
Актуарна поточна вартість такої угоди страхування:
(^Чіч ■ )и< о"-ю>- "ял <*>л.
о
Ця угода є протилежною до угоди страхування на випадок смерті строком на п років з виплатами, що щорічно збільшуються, в тому розумінні, що сума їх функцій виплат є постійною і дорівнює п + 1 для строку в п років.
Усі наведені вище позначення для страхових угод з виплатами в момент смерті зведемо в одну таблицю (табл. 26.1).
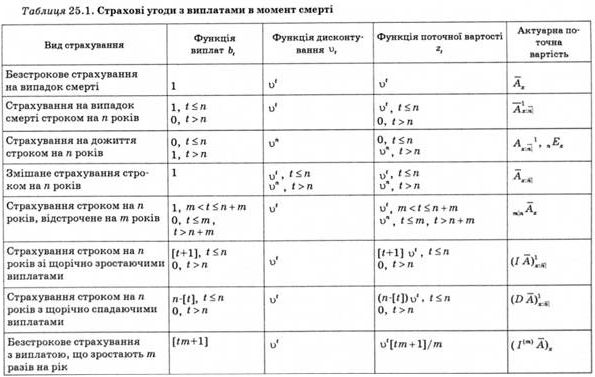
25.2. Страхові угоди з виплатами наприкінці року смерті
Співвідношення між страховими угодами з виплатами в момент смерті й наприкінці року смерті
25.3. Страхові ануїтети
25.4. Нетто-премії
25.5. Нетто-резерви
Висновки
Навчальний тренінг
Розділ 26. МОДЕЛЬ КОЛЕКТИВНОГО РИЗИКУ
26.1. Точні та наближені методи розрахунку ймовірності банкрутства