Загальне землезнавство - Олійник Я.Б. - 4.1. Форма і розміри планети

4.1. Форма і розміри планети

Розуміння того, що Земля — куля, окремі вчені мали ще дві з половиною тисячі років тому. Так, Піфагор (VI ст. до н. е.) вважав, що Земля має форму кулі і вільно та нерухомо висить у центрі Всесвіту. Навколо неї за круговими орбітами рухаються Сонце, Місяць, планети і небесна сфера з розсипаними по ній зірками. Всі вони мають, як і Земля, кулясту форму, тобто найбільш досконалу.

З обчислень розмірів Землі, проведених у стародавні часи, найбільш відомі розрахунки грецького вченого Братосфена (276—194 pp. до н. е.). Зробив він це напрочуд просто. Ератосфену було відомо, що під час літнього сонцестояння в Сієні (нинішньому Асуані) Сонце опівдні знаходиться в зеніті, тому його відображення можна побачити на дні навіть дуже глибокого колодязя, що знаходився на острові в руслі Нілу. В той самий час в Александра промені Сонця падають під кутом 7° 12' — так показали вимірювання, здійснені Ератосфеном за допомогою вертикального обеліска, що знаходився у дворі знаменитої Александрійської бібліотеки, в якій він працював. Маючи ці відомості, Ератосфен пізніше використав добре відому теорему Фалеса, за якою перехресні кути, які утворилися при перетині двох паралельних прямих третьою прямою, рівні між собою. Паралельні лінії утворювали промені Сонця (рис. 3). Сонячні промені, вертикальні до земної поверхні в Сієні, можна було умовно продовжити до центра Землі. До центра Землі можна було продовжити і лінію обеліска, який стояв теж вертикально, але в Александрії. Тоді кут між сонячними променями і вертикальним обеліском повинен бути таким самим, як і кут біля центра Землі між умовно продовженими лініями сонячного променя в Сіені і обеліска в Александрії. Далі потрібно було знайти, якій частині кола дорівнює дуга, що стягує кут між Александрією і Сієною. Ератосфен обчислив, що вона дорівнює 1/50 всієї довжини кола.

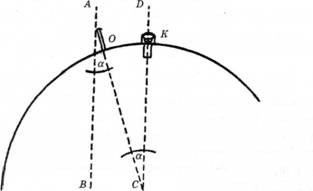
Рис. 3. Розрахунок розмірів Землі, зроблений Ератосфеном:

О — обеліск в Александрії; К — колодязь в Сіені; С — центр Землі; АВ — напрямок сонячних променів в Александрії; DC — напрямок сонячних променів у Сієні; а — перехресні кути

Тепер, щоб визначити довжину, яка відповідає одному градусу, необхідно було знати відстань між Александрією і Сієною. З розповідей мандрівників, які подорожували цим караванним шляхом, Ератосфену було відомо, що ця відстань дорівнює 5000 єгипетських стадій. Таку міру довжини ввели ще вавилонські жерці, які знали основи астрономії. Вони розрахували, що Сонце під час рівнодення описує від сходу до заходу дугу, яка дорівнює 360 діаметрам сонячного диска. Значить, за годину воно проходить дугу" рівну 30 діаметрам, а за дві хвилини — відстань в 1 діаметр. За цей час на верблюді можна проїхати в середньому 157,5 м. Саме таку відстань становила стадія — одиниця довжини, яку використав Братосфен для обчислення розмірів Землі. Довжина кола Землі, за Ератосфеном, виявилася рівною 252 000 стадіям, а її радіус — 6275 кілометрів. На той час — вражаючий результат!

Істотного просування у визначенні форм Землі вдалося добитися в 1735 р. французькому астроному Ж. Рішару, який задумав і здійснив дослід з маятниковим годинником. Рішар встановив, що годинник, який показував точний час у Парижі, в Кайєнні (Французька Гвіана) став відставати на 2 хв. 28 с на добу. Виявлений Рішаром ефект не був несподіваним для вчених того часу. Досягнутий рівень розвитку механіки давав підстави вченим зробити висновок, що внаслідок осьового обертання Землі вона повинна мати форму еліпсоїда. Використовуючи результати спостережень Рішара за ходом годинника, І. Ньютон і його сучасник X. Гюйгенс вперше визначили величину сплюснутості Землі. їх міркування зводилися до такого. Період коливання Т маятника залежить від його довжини l і прискорення сили тяжіння g:

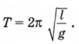
Оскільки Рішар не змінював довжину маятника, а період коливань збільшився (годинник став відставати), прискорення сили тяжіння в Кайєнні повинно було зменшитися в порівнянні з Парижем. Відбувається це з двох причин. По-перше, в міру віддалення від вісі обертання зростає відцентрова сила. По-друге, Земля сплюснута біля полюсів, тому в Кайєнні, яка розташована близько до екватора, маятниковий годинник знаходиться далі від центру Землі і прискорення, що створюється діючою на нього силою тяжіння (згідно із законом всесвітнього тяжіння Ньютона), менше, ніжу Парижі.

За розрахунками Ньютона, величина сплюснутості Землі становила 1/230, що досить добре узгоджується з існуючими нині оцінками. Одержаний Ньютоном результат означав, що екваторіальний радіус Землі на 1/230 більше від полярного.

Дослід Рішара і результати математичних обчислень Гюйгенса і Ньютона показали, що гравітаційні вимірювання — дуже ефективний засіб для визначення форми Землі: порівняння ходу маятникового годинника у різних точках на поверхні Землі, які розташовані на різних широтах" дозволяє визначити сплюснутість Землі. Гравітаційні вимірювання форм Землі були виконані лише у XX столітті.

У XVIII і XIX ст. при визначенні форми Землі головна роль відводилася геодезичним вимірюванням. Основна ідея їх полягала у вимірюванні довжини меридіана і в розрахунках на основі одержаних даних радіусів Землі і сплюснутості. Безпосередньо виміряти повну довжину меридіана було б надзвичайно важко, тому, як правило, обмежували вимірюванням довжини відрізка меридіана, який знаходиться між двома точками з достатньо великою різницею широт. Далі за довжиною дуги обчислюють повну довжину меридіана, а також екваторіальний і полярний радіуси Землі.

Навіть при різниці широт лише в Г довжина дуги меридіана становить близько 111 км, тому виміряти її з необхідною точністю досить складно. Застосування тріангуляції стало способом, який дозволив зводити вимірювання довжин до простих і високоточних вимірювань кутів. Базується тріангуляція на тому, що в будь-якому трикутнику за відомою стороною і двома прилеглими до неї кутами можна обчислити фактичні довжини двох інших сторін. Отже, якщо в якому-небудь місці на Землі виміряти довжину лише однієї сторони то, вимірюючи пізніше тільки кути, можна визначити відстань до будь-якої точки. Довжину першої сторони трикутника (довжину базису) можна визначити з високою точністю.

Винахід способу вимірювання великих відстаней за допомогою тріангуляції прийнято пов'язувати з ім'ям відомого голландського вченого В. Снелліуса. Вимірювання базису В. Снелліус провів у Голландії між Лейденом і Гаагою, де він "побудував" трикутники і визначив місцеположення голландських міст від Алкмара до Бреди та відстань між ними. Широке практичне застосування тріангуляції мало величезне значення для розвитку знань про Землю.

У XVIII ст. великі французькі експедиції провели вимірювання еліпсоїда Землі і визначили на основі результатів цих робіт одиницю вимірювання довжини. Перша французька експедиція відбулася в 1723 р. Але внаслідок помилки в розрахунках форма Землі була визначена неправильно; еліпсоїд виявився витягнутим вздовж осі обертання Землі.

Друге вимірювання довжини меридіана було здійснене на основі результатів ретельно підготовлених експедицій 1736— 1748 pp. Визначити розміри земного еліпсоїда за довжинами дуг меридіанів можна тим точніше, чим більше відрізняються за широтою місця, де проводяться вимірювання. Тому було споряджено дві експедиції: одна працювала поблизу екватора в Перу, друга — поблизу Полярного кола в Лапландії.

Ще більш відомим стало третє вимірювання дуги меридіана, який проходить через Париж. На основі його результатів був створений еталон метра — одиниці довжини. За величину одного метра прийнято одну сорокамільйонну частину довжини паризького меридіана.

Яка ж форма і розміри Землі за сучасними даними? На основі численних геодезичних вимірювань, здійснених для найточнішого відображення загальних особливостей земної поверхні, були запропоновані різні значення параметрів земного еліпсоїда. У країнах Східної Європи для обчислення системи координат, обробки геодезичних даних і проведення картографічних робіт використовують еліпсоїд Ф.М. Красовського.

Він має такі параметри:

Екваторіальний радіус (а) 6 378,2 км

Полярний радіус (b) 6 356,8 км

Різниця між ними (а - b) 21,4 км

Середній радіус, або радіус

рівновеликої кулі 6 371,1 км

Площа поверхні земного еліпсоїда (округлена) 510,0 млн км²

Довжина кола за меридіаном 40 008,5 км

Довжина кола за екватором 40 075,6 км

Полярне сплющення Землі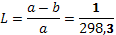

Внаслідок нерівномірного розподілу маси і неоднорідності речовинного складу Землі її форма відхиляється від правильної форми еліпсоїда. На це відхилення впливають також гравітаційні поля Галактики. Справжню форму Землі назвали геоїдом (слово "геоїд" буквально означає землеподібний). Це форма, яку утворила б спокійна поверхня Світового океану, вільна від впливу припливів, течій, відмінностей в розподілі атмосферного тиску. Уявити собі таку поверхню на суші можна, якщо поверхню океану умовно продовжити під континентами. У кожній точці геоїда напрям сили тяжіння перпендикулярний до його поверхні. Геоїд незначно відхиляється від земного еліпсоїда. Підняття геоїда над еліпсоїдом Красовського не перевищують 136 м, опускання — 162 м. При цьому поверхня геоїда здебільшого проходить над океанами і під материками. Це пов'язано з неоднорідною будовою земної кори під океанами і материками.

На основі вивчення даних, отриманих за допомогою штучних супутників Землі, було встановлено полярну асиметрію Землі. Виявилося, що наша планета має форму кардіоїда (серцеподібну форму), причому Північний полюс ц трохи піднятий у порівнянні з Південним приблизно на 70—100 м (рис. 4). Вважають, що полярна асиметрія зумовлена дією гравітаційних полів Галактики на тіло Землі.

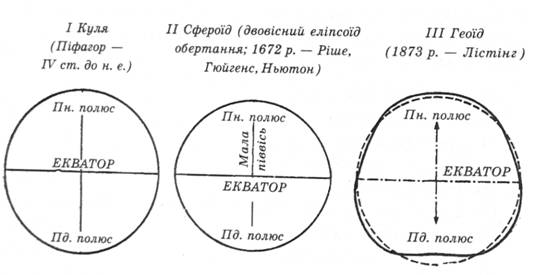
Рис. 4. Уявлення про форму поверхні Землі

Варто зазначити, що справжня форма поверхні Землі відхиляється від будь-якої умовної теоретичної поверхні еліпсоїда чи геоїда. Всі нерівності рельєфу просто неможливо вписати в жодну відому математичну форму. Нагадаємо, що максимальна абсолютна висота фізичної поверхні над середнім рівнем Світового океану становить 8848 м (гора Еверест), найбільша глибина — 11 022 м (Маріанська западина). І все ж, незважаючи на значний перепад абсолютних і відносних висот, спеціалісти знайшли способи для зображення рельєфу на картах з досить високою точністю.