Екологія і організація природоохоронної діяльності - Шматько В.Г. - 7.3. Моделювання в розробці регіональних планів та програм

Розробка планів - процес багатогранний, складний, потребує поєднання інформації з різних галузей суспільно-господарської діяльності, науки, наукових методів дослідження. Сьогодні незмінним у планування є економіко-математичне моделювання на базі електронно-обчислювальної техніки. Завдяки йому підвищується якість планування, скорочуються терміни на трудомісткість виконання розрахунків тощо.

На основі економіко-математичних моделей створена система комплексних народногосподарських матеріальних балансів виробництва важливих видів продукції по галузях та територіальних регіонах, що дає змогу визначити види та обсяги забруднення навколишнього середовища, досягти збалансованості екологічних планів та програм.

Важливою умовою підвищення ефективності охорони довкілля є розробка та впровадження автоматизованих систем управління регіонами. Для моделювання процесів планування та управління виробництвом розробляються економіко-математичні моделі, які дозволяють вивчати економічні процеси. Такі процеси використовуються для аналізу математичних явищ, планування розвитку економічних систем, розробки ефективних методів управління, фізичного моделювання процесів в економічних системах, автоматизації планово-економічних розрахунків.

Модель є елементом загальної методології, яка застосовується у будь-якій сфері наукового пізнання. Моделювання як метод дослідження вважається найбільш універсальним і підлягає додержанню суворих логічних вимог. Але жодна модель не може бути повним віддзеркаленням явища, що вивчається, у всій його складності, тому, що вона абстрактно "описує" реальні процеси і враховує лише основні фактори, тобто типове, що є в досліджуваному явищі. Кількість факторів, що включаються до моделі, відображують ступінь її наближення до реальної дійсності.

Моделювання розглядається не лише як засіб аналізу, а й як база для прийняття конкретних рішень. Економічна інтерпретація математичної структури моделі передбачає уточнення та доповнення основних елементів, зв'язків і відношень об'єктів економіки.

В економіці переважають кількісні залежності статистичних характеристик економічних систем, структури яких мають декілька рівнів організації. У загальному вигляді можна виділити макро- і мікрорівні. Економічна система на макрорівні охоплює народне господарство в цілому, на мікрорівні - окремі підприємства. Характеристики обох рівнів відносно автономні.

Для побудови економічної моделі необхідно зробити якісний аналіз економічного процесу із застосуванням математичних методів (рис. 7.1).

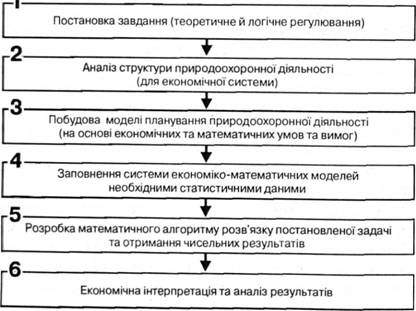
Рис. 7.1. Етапи і послідовність аналізу економічного процесу планування із застосування математичних методів

Науковий характер математичної моделі передбачає її адекватність еколого-економічному процесу, який аналізується, і відповідність таким вимогам:

- дотримання суворої наукової економічної теорії, що розкриває категорії та закономірності розвитку економіки природокористування як бази досліджень;

- відтворення реальної структури економічного процесу у відповідності з принципом структурної подібності;

- забезпечення єдності масштабу та розмірності змінних і постійних величин;

- відбір фактичних даних з урахуванням специфіки зміни економічних параметрів досліджуваного процесу;

- облік принципової різниці між керованими і некерованими величинами;

- визначення граничних умов, у межах яких дійсна дана модель, що задовольняє вимоги, які сформувалися.

Якщо цих умов не дотримано, систему рівнянь не можна розглядати як математичну модель економіки.

Отже, модель - це строго впорядкована теоретична та емпірична інформація, яка включає абстрагування, спрощення та укрупнення чи агрегування; логічну та математичну формалізацію; економічну інтерпретацію математичних перетворень та рішень. Моделювання не може замінити теоретичного аналізу, але є прикладом вираження економічного змісту завдяки мові математики.

Основним елементом будь-якої математичної моделі є її економічні параметри, тобто вимірювальні величини, які характеризують структуру природоохоронної діяльності (по регіонам, окремим підприємствам тощо), її стан, рівень розвитку та процес економічного розвитку. Ці величини створюють базу економічної моделі й є основою для застосування кількісного аналізу економіки.

Кожній математичній величині в економіко-математичних дослідженнях має відповідати певне економічне поняття. Цій закономірності притаманний і зворотний зв'язок: визначення економічних параметрів спрощує побудову математичної моделі, забезпечує відповідну інтерпретацію стану економіки в отриманих математичних результатах. При цьому сукупність економічних параметрів розглядається як взаємопов'язаний об'єктивно існуючий комплекс кількісних характеристик досліджуваних економічних процесів. Вони характеризуються кількісно та структурно, а комплекс параметрів перетворює схему, аналогію, систему рівнянь у дійсну модель, адекватну реальній економічній системі.

Математичні моделі можна поділити на функціональні, які враховують галузеві та міжгалузеві регіональні проблеми розвитку, та оптимізаційні, що дають можливість вибору кращого варіанта за встановленими критеріями.

Існують різні форми моделювання: наочна, фізична, інформаційна, імітаційна.

Наочне моделювання передає зовнішній вигляд об'єкту, допомагає встановити складні технологічні зв'язки. Використовується у проектуванні будівельних робіт.

Фізичне моделювання відображує досліджуваний об'єкт через динаміку фізичних процесів у економіці. Застосовується при побудові електронних аналогових машин для розрахунку сітьових графіків.

Інформаційне моделювання використовує різні графічні та математичні методи відображення певної інформації та процесів її перетворення. У складі інформаційного моделювання розрізняють економіко-математичні моделі, що реалізуються засобами математичного апарату з використанням формул, рівнянь, нерівностей, та графічні моделі, які формуються засобами логічного апарату з використанням графіків, таблиць, схем, креслень.

Математичне моделювання процесів економіки з кількісним аналізом економічних явищ забезпечує оптимальне управління регіональним сільськогосподарським комплексом. Проте використання математики в економіці не обмежується формалізацію зв'язків між її категоріями і отриманням їх точної кількісної характеристики, а й передбачає активне втручання в якісний зміст досліджуваних явищ.

При вирішенні оптимальних завдань на стадії техніко-економічного планування необхідно встановити критерій оптимальності, який математично вважається цільовою функцією. Такими критеріями можуть бути досягнення високих показників рентабельності виробництва, отримання максимального обсягу валової продукції, введенню в дію виробничих потужностей, основних фондів, будівельних об'єктів.

Процес пошуку оптимального управлінського рішення пов'язаний з переглядом множини альтернативних рішень.

Завданням прийняття рішення на базі економіко-математичної моделі є знаходження оптимального (екстремального) рішення, на підставі якого досягається мета дослідження.

Економіко-математична модель доповнюється вибором граничних обмежень. Практично це єдине завдання, адже без вихідних граничних обмежень не можна побудувати економіко-математичну модель. Тому критерій оптимальності та обмеження моделі, як правило, обираються одночасно у взаємозв'язку.

Під обмеженням моделі розуміють кількісні та якісні обмеження ресурсів, економія, найкращий розподіл, ефективне використання тощо.

При вирішенні техніко-економічних завдань методами оптимального планування в якості обмежень моделей можуть виступати різні нормативи використання виробничих та земельних ресурсів, постачання матеріалів тощо.

Економіко-математичні моделі розв'язуються різними математичними методами у вигляді алгебраїчних рівнянь (нерівностей) чи їх систем. Рівняння чи нерівності в залежності від характеру явища, яке вони відображують, можуть бути лінійними (якщо економічні явища носять статичний характер) чи диференціальними, інтегральними, функціональними та іншими (якщо економічні явища розглядаються в динаміці). Найбільш поширеним є математичний аналіз процесів та явищ, економічні моделі яких виражаються системою лінійних рівнянь чи нерівностей.

З урахуванням принципів моделювання економіко-математичну модель у загальному вигляді можні зобразити такою системою нерівностей:

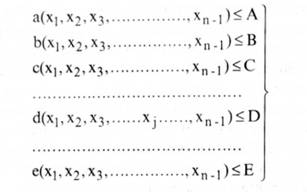
де a, b, с,d,е - різні нормативи використання виробничих ресурсів;

Х|, х2, х3,Xj,хп_| - невідомі змінні, які необхідно визначити під час вирішення завдання;

А, В, С, D, Е - константи, що характеризують задану величину виробничих ресурсів.

Окрім системи рівностей задана цільова функція:

b(X], х2, х3,............, xn_j) = z -> max чи min. r. 7.2.

Процес оптимізації у цих моделях зводиться до визначення таких додатних значень невідомих х0,, х°2, х°3,x°j,х°п_і" які б задовольняли систему вихідних обмежень та приводили до екстремального значення цільову функцію.

Графічна модель виражається кількома формами, найпростішою серед яких є таблиця - числові дані, розташовані колонками в певному порядку.

Графік як форма графічної моделі дає геометричне зображення функціональної залежності.

При плануванні розвитку сільського господарства та АПК в регіоні використовуються різні графіки з різним ступенем деталізації - від планування інвестицій по окремих об'єктах та виробництвах до планування розвитку сільського господарства й агропромислового комплексу в цілому по регіону на різні проміжки часу (від годинних до перспективних). Графіки можуть бути подані у вигляді лінійної моделі, циклограми чи сітьової моделі.

Лінійні графіки (графіки Ганта) використовують для зображення окремого виду робіт у вигляді прямих ліній, які характеризують їх тривалість в обраному масштабі часу.

У графіках циклограм по осі абсцис відкладається час, а по осі ординат - одиниці виміру продукції. їх використовують для графічного відображення потоку, що розглядається як процес, змінний у часі та просторі.

Сітьова модель стріловою діаграмою схематично показує технологічну та організаційну послідовність виконання робіт. Графічно така модель має вигляд стрілок та кругів.

Третьою формою графічної моделі є схема. Схемою називають зображення, опис, викладення чи креслення, за допомогою яких наочно відтворюється зв'язок чи залежність окремих частин досліджуваної системи. Більш досконалим різновидом є блок-схема, в якій окремі елементи поєднуються в блоки. Блок-схеми використовуються для побудови логічних моделей, які через логічні закони мислення передають об'єктивний зміст досліджуваних предметів і тим самим сприяють пізнанню різних форм дійсності. Логічна модель може бути представлена оперативною блок-схемою, коли окремі її елементи об'єднані в блоки за принципом виконання аналогічних функцій. Логічні моделі, що використовуються для узгодження потоків вхідної та вихідної інформації в автоматизованих системах управління, називаються логічно-інформаційними. Вони також мають вигляд блок-схем.