Теорія економічного аналізу - Купалова Г.І. - 13.6. Теорія масового обслуговування

На практиці при вивченні операцій часто доводиться мати справу з системами, призначеними для багаторазового використання при розв'язанні однотипних задач. Процеси, які виникають при цьому отримали назву процесів обслуговування, а системи – систем масового обслуговування. Прикладами таких систем є ремонтні майстерні, телефонні системи, обчислювальні комплекси, магазини тощо.

Кожна система масового обслуговування складається з певного числа обслуговуючих одиниць, зокрема приладів, при-

строїв, пунктів, станцій, які називають каналами обслуговування. Каналами можуть виступати продавці, перукарі, обчислювальні машини, точки продажу, лінії зв'язку та ін. За кількістю каналів системи масового обслуговування поділяються на одноканальні (один канал) та багатоканальні (декілька каналів).

Заявки надходять в систему масового обслуговування зазвичай нерегулярно, а випадково, утворюючи так званий випадковий потік заявок (вимог ). Обслуговування заявок триває також якийсь випадковий час. Випадковий потік заявок і часу обслуговування призводить до того, що система масового обслуговування виявляється завантаженою нерівномірно: в якісь періоди часу накопичується дуже велика кількість заявок, а в інші періоди система працює з неповним завантаженням або простоює. Для того, щоб максимально оптимізувати, регулювати ці процеси шляхом прийняття зважених та обґрунтованих управлінських рішень використовується теорія масового обслуговування.

Теорія масового обслуговування – теорія, яка вивчає статистичні закономірності в масових операціях, що складаються з великого числа однорідних елементарних операцій. До них, зокрема належать: складання однотипних деталей на конвеєрі, видача інструментів, ремонт верстатів, робота телефонної станції, обслуговування покупців у магазині, в білетних касах, клієнтів у перукарнях, технічне обслуговування машин та обладнання тощо.

Синонімом теорії обслуговування є теорія черг. У системах масового обслуговування, в яких заявки на елементарні операції надходять у випадкові моменти часу або обслуговуються протягом випадкових проміжків часу, поява черг – неминуче зло. За великої кількості каналів обслуговування (ремонтних бригад, продавців, телефоністок і т. п.) система зазнає збитків через можливі тривалі простої каналів. За малої кількості каналів обслуговування, збитки системи спричиняють черги, які накопичуються.

Завдання теорії масового обслуговування – вивчити статистичні закономірності вхідного потоку заявок на елементарні операції та тривалість обслуговування заявок, а також дати оцінку якості систем обслуговування (з'ясувати пропускну здатність) за різних правил формування черг. Черги можуть бути організовані по різному – з обмеженою та необмеженою довжиною черги, з обмеженим часом очікування та ін.

Предметом теорії масового обслуговування є побудова математичних моделей, які пов'язують задані умови роботи систем масового обслуговування (число каналів, їх продуктивність, характер потоку, заявок тощо) з показниками ефективності цих систем, що описують їх здатність справлятися з потоком заявок.

Під потоком подій розуміють послідовність однорідних подій, які настають одна за другою в якісь випадкові моменти часу (наприклад, потік викликів на телефонній станції, потік відмовлень БВМ, потік покупців тощо).

Потік характеризується інтенсивністю (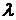) – частотою появи події або середнім числом подій, які надходять в систему масового обслуговування за одиницю часу.

В ролі показників ефективності систем масового обслуговування можуть використовуватися такі:

– середнє (тут і далі середнє як математичне очікування відповідних випадкових величин) число заявок, які обслуговуються за одиницю часу;

– середня кількість заявок у черзі;

– середній час чекання на обслуговування;

– ймовірність відмови в обслуговуванні без чекання;

– ймовірність того, що число заявок в черзі перевищить певне значення тощо.

Системи масового обслуговування поділяються на два основні типи (класи): з очікуванням (чергою) та з відмовленнями. У системі масового обслуговування з очікуванням заявка, яка надійшла в момент зайнятості каналів, не відправляється, а стає в чергу на обслуговування.

В системах з відмовленням заявка, яка надходить в момент, коли всі канали зайняті, отримує відмовлення та покидає систему, не приймаючи участі в подальшому процесі обслуговування (наприклад, заявка на телефонну розмову в момент, коли всі канали зайняті, отримує відмовлення і залишає систему не обслуженою).

У ролі показників ефективності системи масового обслуговування з відмовленнями застосовуються такі:

1. Абсолютна пропускна здатність (А) – показник, який показує середню кількість заявок, що обслуговуються за одиницю часу. Він розраховується за формулою

,

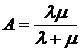де 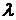– інтенсивність потоку заявок;

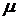– інтенсивність потоку обслуговування.

При цьому інтенсивність потоку обслуговування є оберненою величиною до середнього часу обслуговування ():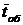

.

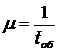2. Відносна пропускна здатність (Q) – показник, що характеризує середню частку заявок, яка надійшла та обслуговується системою. Обчислюється за формулою

.

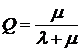3. Ймовірність відмови (Р_від) – величина, яка характеризує ймовірність того, що заявка залишить систему масового обслуговування не обслуженою. Показує частку заявок, яким буде відмовлено в наданні відповідної послуги.

.

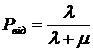4. Середнє число зайнятих каналів (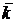) (для багатоканальної системи). Цей показник розраховується у такий спосіб:

.

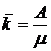Визначається також інтенсивність навантаження каналу – р (або приведена інтенсивність потоку заявок) – це показник, який виражає середню кількість заявок, яка надходить за середній час обслуговування однієї заявки. Він розраховується за формулою

.

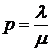В багатоканальних системах масового обслуговування з граничними ймовірностями використовують формули для граничних ймовірностей стану, які отримали назву формул Ерланга на честь А.К. Ерланга (кінець XIX – початок XX ст.) – датського інженера, математика, засновника теорії масового обслуговування.

Ймовірність відмови системи масового обслуговування – це гранична ймовірність того, що всі п каналів системи будуть зайняті, тобто:

;

;

, , …, , …, .

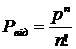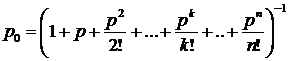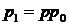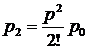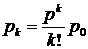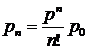Відносна пропускна здатність – ймовірність того, що заявка буде обслужена визначається:

.

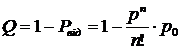Абсолютна пропускна здатність розраховується:

.

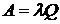Для класифікації систем масового обслуговування важливе значення має дисципліна обслуговування, яка визначає порядок вибору заявок з числа тих, що надійшли, та порядок розподілу їх між вільними каналами. За цією ознакою обслуговування заявки може бути організовано за принципами черговості надходження: в порядку надходження (з початку) або навпаки обслуговуються ті, які надійшли в кінці (з кінця), з пріоритетом обслуговування (в першу чергу обслуговуються найважливіші заявки).

Приклад. Заявки на телефонні переговори на переговорному пункті надходять з інтенсивністю 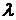, яка дорівнює 80 заявок на годину, а середня тривалість розмови по телефону .

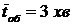1. Визначити показники ефективності роботи системи масового обслуговування (переговорного пункту) за наявності одного телефонного номера.

2. Визначити оптимальну кількість телефонних номерів на переговорному пункті, якщо умовою оптимальності вважати

задоволення в середньому з кожних 100 заявок не менше 80 заявок на переговори.

Розв'язання

1. Розрахуємо інтенсивність потоку обслуговування:

.

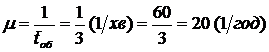2. Визначимо відносну пропускну здатність системи масового обслуговування:

.

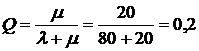Це означає, що в середньому тільки 20% заявок, які надходять, будуть задоволені й за ними будуть надані послуги, тобто здійсняться переговори по телефону.

3. Ймовірність відмови в обслуговуванні (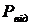) становитиме:

.

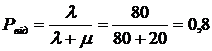Отже, в середньому 80% заявок, які надійдуть на переговори, отримають відмову в обслуговуванні.

4. Абсолютна пропускна здатність системи масового обслуговування – переговорного пункту дорівнюватиме

.

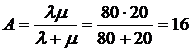Таким чином, в середньому за годину будуть обслужені 16 заявок на переговори.

З цього можна зробити висновок, що за наявності тільки одного телефонного номера переговорний пункт буде погано справлятися з потоком заявок.

Для виконання другого завдання задачі – визначення оптимального числа номерів на телефонній станції, слід перш за все проаналізувати інтенсивність навантаження каналу.

5. Обчислимо інтенсивність навантаження каналу:

.

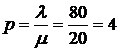Тобто, за час середньої за тривалістю телефонної розмови 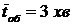надходить в середньому 4 заявки на переговори.

6. Для одержання характеристик системи (переговорного пункту) та вибору оптимального варіанта кількості номерів слід поступово збільшувати число каналів (телефонних номерів) n = 2,3,4, ..., перетворюючи таким чином наявну систему масового обслуговування з одноканальної в багатоканальну. Тоді відносна пропускна здатність становитиме:

;

;

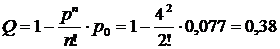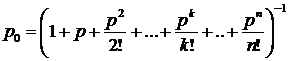за ; .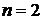

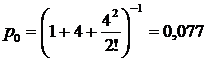Абсолютна пропускна здатність дорівнюватиме:

.

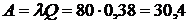Аналогічно розрахуємо основні характеристики системи масового обслуговування для 3, 4, 5, 6 каналів обслуговування (номерів телефонів) та зведемо їх у табл. 13.5.

Таблиця 13.5. Основні характеристики обслуговування заявок на переговори переговорним пунктом залежно від кількості номерів

Отже, за умовами оптимальності Q³=0,8, тому на переговорному пункті необхідно встановити 3 телефонні номери (в цьому випадку Q = 0,80). Це означає, що за годину будуть обслуговуватися в середньому 64 заявки (А = 64), а середня кількість зайнятих номерів (каналів) дорівнюватиме

.

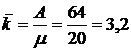Не дивлячись на велике значення теорії ігор для прийняття управлінських рішень, вона не має універсального характеру. Одним із основних обмежень її застосування є те, що в цій грі наявний єдиний показник виграшу як характеристика ефективності. Проте на практиці при вирішенні більшості економічних завдань зустрічаються декілька показників ефективності. Крім того, в економіці здебільшого виникають такі ситуації, коли інтереси партнерів не мають антагоністичного характеру. Ці особливості слід враховувати аналітику при виборі методів дослідження тих чи інших економічних явищ і процесів.