Логіка - Дуцяк І.3. - 2.2. Суперечність між твердженнями тексту

Нижче описано метод виявлення логічно хибних тверджень у послідовності пов'язаних тверджень, тобто таких, які містять однакові прості твердження-складники. Наприклад, твердження Якщо в мережі є напруга і нема розриву, то електроприлад працює; У мережі є напруга є пов'язаними, оскільки і в першому, і в другому міститься однакове просте твердження (У мережі є напруга). Натомість твердження Сьогодні четвер; Земля обертається навколо Сонця не є пов'язаними.

Інструменти. Алгоритм виявлення суперечності у послідовності пов'язаних тверджень

Для виявлення суперечності, послідовно виконують такі дії:

1. Записують послідовність тверджень у символьному вигляді.

2. Фіксують, що кожне з тверджень послідовності подано як фактично істинне.

3. Визначають значення істинності простих тверджень-складників, зафіксованих кожним твердженням послідовності.

4. Порівнюють значення істинності простих тверджень -складників, зафіксовані кожним із тверджень послідовності. У разі, коли якимось твердженням послідовності певне просте твердження подано з іншим значенням істинності, аніж це було у попередніх твердженнях, то твердження, яке "внесло" суперечність, зачислюють до логічно хибних.

Приклад 1: виявлення логічно хибних тверджень у послідовності тверджень: Неправда, що особу А цікавить мовознавство; Особу А цікавить мовознавство:

1. Записуємо цю послідовність тверджень у символьному вигляді:

2. Фіксуємо під кожним із тверджень, що його подано як фактично істинне:

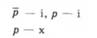
3. Визначаємо значення істинності простих тверджень-складників, зафіксованих кожним твердженням послідовності (в аналізованому прикладі це стосується лише першого твердження послідовності). У стовпці під першим твердженням послідовності записуємо р - х.

4. На підставі порівняння значень істинності твердження р, зафіксованих першим і другим твердженнями послідовності, висновуємо, що друге твердження є логічно хибне, оскільки другим твердженням послідовності зафіксовано інше значення фактичної істинності твердження р, аніж першим.

Приклад 2: виявлення логічно хибних тверджень у послідовності тверджень: Сьогодні четвер; Якщо сьогодні четвер, то завтра п'ятниця; Неправда, що завтра п'ятниця:

1. Уводимо позначення сьогодні четвер -р, завтра п'ятниця - записуємо аналізовану послідовність тверджень у символьному вигляді:

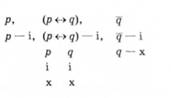
2. Зафіксовуємо під кожним із тверджень послідовності, що кожне з них подано як фактично істинне (другий рядок праворуч).

3. Визначаємо значення істинності простих тверджень-складників, зафіксованих кожним твердженням послідовності. Перше твердження послідовності є простим, тому щодо нього не треба виконувати подальшого аналізу. Друге твердження послідовності містить еквіваленцію. З таблиці істинності еквіваленції отримуємо, що в разі, коли складне твердження з еквіваленцією є істинним, його твердження-складники мають однакові значення істинності, що й фіксуємо у стовпці під твердженням (р <-" д). З таблиці істинності заперечення отримуємо, що в разі, коли складне твердження з цим терміном є істинним, то його твердження-складник хибний. Це значення істинності твердження о; записуємо у стовпці під третім твердженням послідовності.

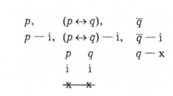
4. Порівнюємо значення істинності простих тверджень-складників, зафіксовані кожним із висловів послідовності. Зіставляємо значення істинності, зафіксовані першим і другим твердженнями послідовності.

Першим твердженням послідовності твердження р подано як істинне, а другим зафіксовано, що твердження р може бути як істинним (перша комбінація значень істинності), так і хибним (друга комбінація значень істинності). Оскільки першим твердженням послідовності однозначно зафіксовано, що твердження р є істинним, то ту комбінацію значень істинності р і д, в якій обидва ці твердження є хибними, викреслюємо. Цей крок відтворено на схемі праворуч. Між першим і другим твердженнями послідовності суперечності немає.

Далі аналізуємо відношення між значеннями істинності простих тверджень, зафіксовані першим і третім твердженнями послідовності. Оскільки перше і третє твердження послідовності не є зв'язаними, тобто не містять однакових тверджень-складників (це твердження різного змісту), то між ними не може бути суперечності (у межах аналізованого типу задач).

Після цього порівнюємо значення істинності, зафіксовані другим і третім твердженнями послідовності. Другим твердженням послідовності зафіксовано, що твердження д є істинним, а третім - як хибне. Суперечність внесена третім твердженням послідовності, тому робимо висновок, що третє твердження послідовності є логічно хибним.