Логіка - Дуцяк І.3. - Інструменти. Алгоритм виявлення можливості формулювання правила виведення (у разі, якщо засновки довільної складності)

1. Записуємо засновки у символьному вигляді.

2. Кожен зі засновків фіксуємо як фактично істинний.

3. Будуємо таблицю істинності того з засновків, який містить два прості твердження-складники.

4. У таблиці істинності викреслюємо ті рядки, в яких кожен зі засновків має інше значення істинності, ніж зафіксоване у пункті 2.

5. Виявляємо на підставі аналізу не викреслених рядків таблиці істинності, чи можна щось однозначно стверджувати про значення істинності простого твердження, значення істинності якого не зафіксовано в засновках у явному вигляді. У разі позитивної відповіді на це питання формулюємо відповідне правило виведення. В іншому випадку робимо висновок: з цих засновків однозначного висновку зробити не можна.

6. За наявності висновку в символьному вигляді формулюємо його словесно.

Проаналізуємо такі засновки:

Приклад 1. Засновки: Якщо падає дощ, то асфальт мокрий. Падає дощ:

1. Записуємо ці засновки в символьному вигляді. Приймаємо такі позначення: падає дощ - р; асфальт мокрий - q. У такому разі засновки в символьному вигляді записуємо так: (р -> д), р.

2. Кожен із наявних засновків фіксуємо як фактично істинний: (р -> о;) - і, р - і.

3. Будуємо таблицю істинності того з засновків, який містить два прості твердження-складники, тобто твердження (р д):

4. У таблиці істинності викреслюємо ті рядки, у яких кожен зі засновків має інше значення істинності, ніж зафіксоване у пункті 2. Отже, треба викреслити другий рядок таблиці, оскільки це варіант, за яким твердження (р -> ф є хибним, а в пункті 2 однозначно зафіксовано, що це твердження істинне. Викреслюємо також третій і четвертий рядки, оскільки це варіанти, за якими твердження р є хибним. У підсумку отримаємо таблицю в такому вигляді:

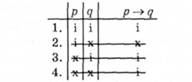
5. В отриманій таблиці залишився один невикреслений рядок, з якого висновуємо, що твердження д, значення істинності якого не міститься в засновках у явній формі, повинно бути однозначно істинним. Тому можемо сформулювати правило виводу:

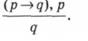
6. Формулюємо висновок у словесному вигляді, повернувши символу д значення, надане йому в процесі виконання першого пункту. Отримуємо висновок: "Асфальт мокрий".

Приклад 2. Засновки: Якщо падає дощ, то асфальт мокрий. Неправда, що падає дощ:

1. Записуємо засновки в символьному вигляді, прийнявши ті самі позначення: падає дощ - р; асфальт мокрий - д. У такому разі засновки матимуть вигляд (р д), р.

2. Кожен із наявних засновків фіксуємо як фактично істинний: (р -> д) - і, р - і.

3. Будуємо таблицю істинності того з засновків, який містить два прості твердження-складники, тобто твердження (р -> д):

4. У цій таблиці істинності викреслюємо ті рядки, в яких кожен зі засновків має інше значення істинності, ніж зафіксоване у пункті 2. Отже, потрібно викреслити другий рядок таблиці, бо це варіант, за яким твердження (р -> д) хибне, а у пункті 2 однозначно зафіксовано, що це твердження є істинним. Оскільки фактично істинним подано вислів р, а в таблиці такого твердження нема (в таблиці є лише значення істинності твердження р), то визначаємо значення істинності твердження р на тій підставі, що твердження р подане як істинне. У такому разі твердження р є хибним: р - х. Тому ті рядки, де р хибне, залишаємо, а ті, де значення істинності твердження р позначено символом і (істинно), викреслюємо. Отже, викреслюємо тільки перший рядок, оскільки це варіант, за якими твердження р є істинним. У підсумку отримаємо таблицю в такому вигляді:

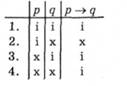
5. В отриманій таблиці залишилося два невикреслених рядки, відповідно до яких вислів д може бути як істинним, так і хибним. Тому однозначний висновок про значення істинності вислову д отримати не можна.

Інструменти. Алгоритм виявлення можливості формулювання правила виведення (у разі, якщо засновки довільної складності)

Нехай задано засновки (р V д) і (д -> г). Потрібно знайти висновок щодо можливих поєднань значень істинності висловів ріг.

1. Будуємо таблицю істинності засновків:

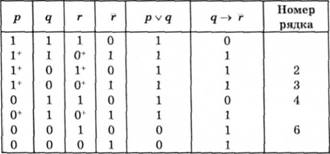
2. Виділяємо ті рядки таблиці, в яких усі засновки є одночасно істинними. У наведеному прикладі в останньому стовпці таблиці ці рядки позначено цифрами 2, 3, 4, 6.

3. У цих рядках виділимо значення змінних, які повинні ввійти в шукану формулу. В аналізованому прикладі виділяємо знаком значення змінних р і г у рядках 2, З, 4 і 6.

4. Отримано такі поєднання значень істинності висловів р і г: 11, 10, 01. Зафіксувавши ці значення в таблиці істинності, отримаємо висновок: р V г.