Логіка - Дуцяк І.3. - 3.3. Відношення логічного випливання та правила виведення

За алгоритмом, описаним у попередньому параграфі, можна побудувати всі можливі правила для кожного з логічних термінів. Ці правила (за спостереженнями автора) самостійно формулюють уже діти середнього шкільного віку, а мислять, несвідомо їх використовуючи, мабуть, уже діти дошкільного віку. Сформулюємо їх найдоступніше, тобто в такому вигляді, в якому вони стануть очевидними не тільки кожному дорослому, а й дитині. (У символьному вигляді правила наведені як відношення логічного випливання).

1. Правило для диз'юнкції

Якщо є принаймні один з двох об'єктів і якогось одного з них нема, то є інший об'єкт.

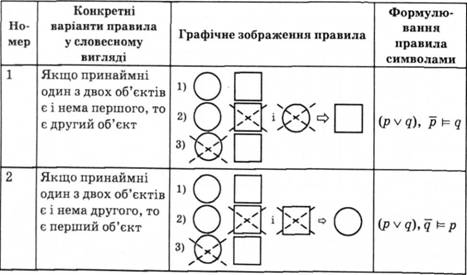
2. Правило для антикон'юнкції

Якщо нема принаймні одного з двох об'єктів і якийсь один з них є, то іншого об'єкта нема.

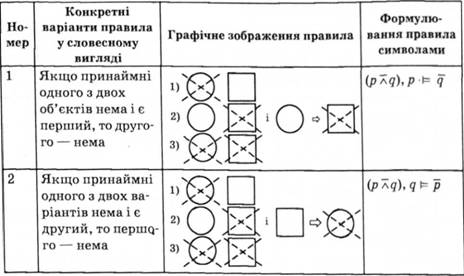
3. Правило для сильної диз'юнкції

Якщо є тільки один з двох об'єктів і якийсь із них є або нема, то, відповідно, іншого об'єкта нема або він є.

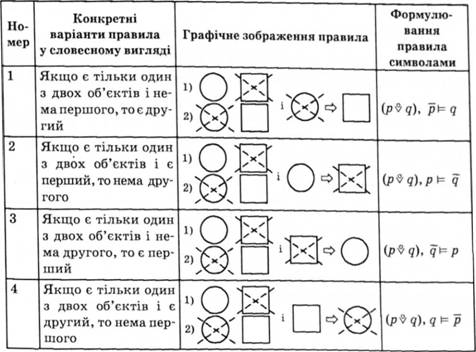
4. Правило для імплікації

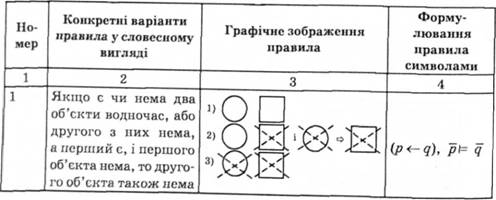
Якщо є чи нема два об'єкти водночас або першого з них нема, а другий є, і є перший або нема другого об'єкта, то, відповідно, є другий або нема першого об'єкта.

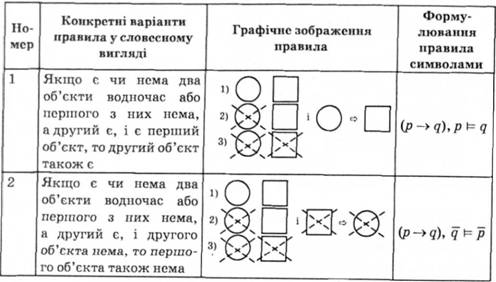
5. Правило для реплікації

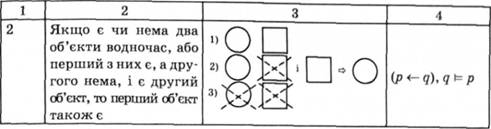
Якщо є чи нема два об'єкти водночас, або перший з них є, а другого нема, і першого нема, або другий є, то, відповідно, нема чи є інший.

6. Правило для еквіваленції

Якщо є чи нема два об'єкти водночас, і якийсь із них є або нема, то, відповідно, інший об'єкт також є або його нема.

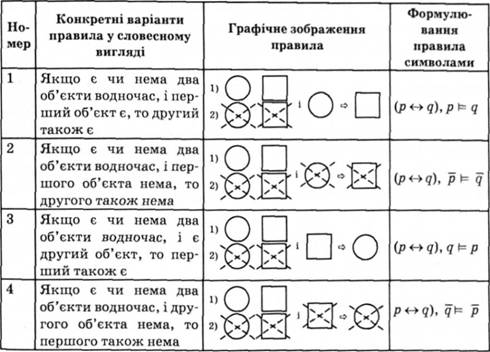
Окрім цих правил, є ще інші. Наведемо деякі.

Правило транзитивності імплікації

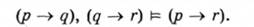
Правило контрапозиції

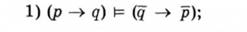
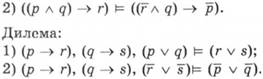
3.3. Відношення логічного випливання та правила виведення

У процесі міркувань стосовно певних тверджень ми фіксуємо, що вони випливають з інших. Перш ніж дати визначення логічного випливання, введемо такі позначення: позначимо твердження довільної структури символами А, В,... (це змінні, значенням яких є прості або складні твердження).

Логічне випливання - це відношення між послідовністю тверджень А19 А2> ... А., які є частиною послідовності Ау9 А29... А., В та твердженням В, яке полягає в тому, що у всіх випадках, коли кожне з тверджень А,, А0,... А є істинним, твердження В також істинне. У такому випадку кажуть, що твердження В (висновок) випливає з тверджень А.9 Ао9 ...А. (засновки). Цей факт записують виразом

А1, А2, ... А.j = В.

Отже, символ 1= позначає не операцію над твердженнями, а відношення між ними.

У разі, коли між твердженнями наявне таке відношення і коли кожне з тверджень Аі9 А2, ... А. є фактично істинним, можна стверджувати істинність твердження В. В інших випадках, коли щонайменше один зі засновків хибний, висновок може бути як істинним, так і хибним. Оскільки висновок не може бути хибним у разі істинних засновків, то можна сказати, що істинність засновків є достатньою умовою для істинності висновку. Отже, якщо послідовність тверджень А., А99 ... А., В записати одним складним твердженням, то між засновками та висновком буде імплікація. Оскільки умовою істинності висновку є істинність кожного

з засновків, то під час запису засновків у формі складного твердження вони повинні бути з'єднані кон'юнкцією. У підсумку послідовність тверджень, у якій останнє випливає з попередніх, можна записати таким складним твердженням:

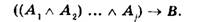
Останній вираз фіксує не послідовність тверджень, між останнім з яких та попередніми наявне відношення логічного випливання, а лише складне твердження, яке відповідає зазначеній послідовності тверджень. Однак встановлені таким способом логічні зв'язки, якими послідовність тверджень об'єднано в одне складне твердження, дають змогу відтворити відношення між значеннями істинності засновків та висновку.

З огляду на те, що, з одного боку, між висновком і засновками є зв'язок достатньої умови (імплікація), тобто все складне твердження хибне тільки в разі істинності антецедента (засновків) і хибності консеквента (висновку), а, з іншого, - за визначенням логічного випливання, консеквент (висновок) не може бути хибним у разі істинного антецедента (засновків), отримуємо таке: прості твердження, які є елементами засновків і висновку, повинні бути з'єднані такими зв'язками, за яких не існували б випадки, коли за істинних Аі9 А2> ...А. було б хибним В. Іншими словами, вираз

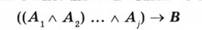
повинен бути законом.

Це дає змогу перевірити, чи справді між певною послідовністю тверджень і твердженням, яке пропонують як таке, що випливає з цієї послідовності, наявне відношення випливання. Для цього послідовність тверджень, наприклад, А , А9У В, треба записати у формі складного твердження

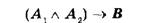
і з'ясувати, чи є цей вираз законом. Якщо це так, то можна бути переконаним, що твердження В випливає з тверджень ¿1" л2.

Проаналізуємо такий приклад: нехай маємо послідовність тверджень (р -" д)9 р9 д. Чи твердження д випливає з тверджень (р -> д), р, тобто чи істинним є складне твердження, що відповідає виразу

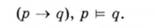
Запишемо наведену послідовність тверджень у формі відповідного складного твердження

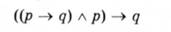
і з'ясуємо табличним методом, чи є отримане складне твердження законом:

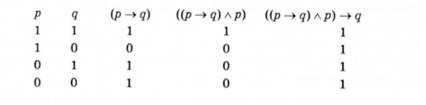
Як бачимо з таблиці істинності, в усіх випадках, коли обидва засновки є одночасно істинними (такий випадок у цьому прикладі тільки один), твердження д також істинне. Оскільки випадків, коли антецедент істинний, а консеквент (висновок) хибний, немає, то це складне твердження є законом. У підсумку можна зробити висновок, що у послідовності висловів (р -> д), р, д твердження д випливає з тверджень (р -> д), р.

Подібно виконують аналіз, коли висновок про випливання певного твердження зроблено з одного засновку. Нехай маємо послідовність тверджень (р л д), р. Чи випливає р з (р л д)?

Побудуємо таблицю істинності відповідного складного твердження (р л д) -> р:

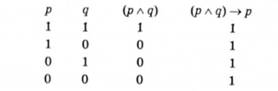
Як і в попередньому випадку, можна стверджувати, що твердження р випливає з твердження (р л q).

Відношення логічного випливання зумовлює можливість виведення знань. На підставі цього відношення можна сформулювати правила, згідно з якими замість одного твердження можна записати інше, так що нове твердження завжди буде істинним у разі істинності того твердження, з якого воно випливає. Усі послідовності тверджень, у яких між останнім і попередніми наявне відношення логічного випливання, можна записати як правила виведення, відповідно до яких можна виконувати перетворення тверджень, тобто виведення нових тверджень.

Для запису правил виведення в поданих вище виразах замість пропозиційних змінних запишемо символи Л, В, які позначають довільні твердження (прості або складні); крім того, нове твердження, тобто висновок, запишемо під засновками, розділивши їх лінією. У такому разі з виразу (р -> g), р t= д отримаємо правило виведення, яке називають модус поненс (modus ponens):

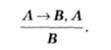
ОЗНАЧЕННЯ

Аксіоматична система - система, в якій висновки отримують із завжди істинних тверджень, унаслідок чого висновки будуть з необхідністю істини.

Антитеза - твердження, яке суперечить тезі.

Виведення - дія (послідовність дій), у результаті виконання якої з одних знань за певними правилами отримують інші знання.

Вивід - сукупність засновків і висновків.

Вивідність - відношення певного твердження до множини інших тверджень, яке полягає в тому, що воно може бути отримане зі згаданої множини тверджень у результаті застосування правил виведення.

Висновок - те нове знання, яке отримують унаслідок виведення.

Дедукція - виведення, в результаті якого у висновку отримують знання, які в неявному вигляді містилися в засновках.

Демонстрація - дії, якими обґрунтовують істинність певних тверджень.

Доведення - обґрунтування істинності певного попередньо заданого твердження (тези) логічними діями.

Засновки - твердження, на підставі яких отримують нове знання.

Логічне випливання - відношення певного твердження до множини інших тверджень, яке полягає в тому, що це твердження є необхідно істинним, якщо істинним є кожне твердження зі згаданої множини тверджень.

Натуральне виведення - отримання висновків з припущень, унаслідок чого істинність висновків залежить від істинності засновків.

Непряме доведення - обґрунтування істинності певного попередньо заданого твердження (тези) шляхом отримання у висновку суперечливого до тези твердження як хибного (логічне обґрунтування хибності антитези).

Правило виведення - зафіксована знаками можливість заміни одних виразів іншими зі збереженням певних ознак цих виразів (зокрема, значення істинності).

Правильний вивід - вивід, виконаний відповідно до правил.

Пряме доведення - обґрунтування істинності певного попередньо заданого твердження (тези) шляхом отримання її як висновку з підібраних аргументів.

Спростування - обґрунтування хибності певного попередньо заданого твердження (тези) логічними діями.

Теза - попередньо задане твердження, істинність якого обґрунтовують.