Логіка - Дуцяк І.3. - 8.2. Припущення як множина дедуктивних висновків

У деяких випадках унаслідок дедуктивного виведення отримують один висновок, однак трапляється, коли в разі дедукції отримують множину можливих висновків, яка містить більше одного елемента.

Проаналізуємо, наприклад, таку послідовність тверджень, унаслідок узгодження знань у якій (чи внаслідок виявлення можливості формулювання правила виведення) буде отримано більше одного можливого висновку, кожен із яких набуває статусу гіпотези. Нехай комерсант формулює твердження про можливі результати комерційної діяльності. Це твердження має такий вигляд: Прибуток або втрата. Після попереднього підрахунку він стверджує, що втрати немає. Отже, маємо текст з двох речень: Прибуток або втрата. Неправда, що є втрата.

Запишемо цей текст у символьному вигляді. Позначимо прості твердження символами: прибуток - р, втрата - д. У цьому разі аналізований текст запишемо так: (р л д), д. Зробимо другий крок - зафіксуємо, що кожне з тверджень тексту "подано" як фактично істинне:

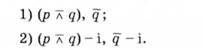
Для кожного складного твердження тексту (в аналізованому тексті обидва твердження складні) виявимо значення істинності простих тверджень-складників. Для цього з таблиць істинності диз'юнкції та заперечення випишемо ті значення істинності аргументів, за яких функція набуває значення "істинно":

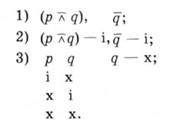
Четвертим кроком виконаємо узгодження значень істинності однакових тверджень-складників, що містяться в різних твердженнях тексту. Першим твердженням послідовності твердження д подано як такс, що може бути як істинним, так і хибним. Другим твердженням послідовності значення істинності цього твердження уточнено - воно хибне. Отже, серед трьох варіантів значень істинності тверджень рід, зафіксованих першим твердженням послідовності, треба вилучити ті, в яких твердження д не хибне, тобто істинне:

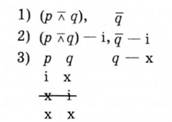
Унаслідок узгодження знань виявлено таке. Суперечностей у тексті нема. Множина несуперечливих значень істинності тверджень містить два варіанти таких значень:

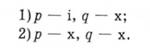
Кожному із цих двох варіантів можна надати статус гіпотези і виявити спеціальними пізнавальними діями значення фактичної істинності цих гіпотез.

Для побудови правил формування припущень проаналізуємо можливість набуття двохаргументними булевими функціями значення 1 для більш ніж двох варіантів значень аргументів. Імовірнісне знання зафіксоване 11 з 15 бінарних логічних термінів. Це стосується функцій /3, від /6 до /7 та від І9 До 15. Кожною з цих функцій позначають, що аргументи хіу мають більше одного варіанта значень істинності.

Знання варіантів значень істинності аргументів для того чи іншого логічного терміна є підставою для формування правил генерування припущень. Як приклад створення методів формування припущень виявимо всі припущення, які можна сформувати на підставі диз'юнктивного твердження. Нехай маємо твердження У мережі розрив або нема напруги, яким пояснюють той факт, що лампочка в кімнаті не засвітилась після того, як увімкнули вмикач. Мовлячи це диз'юнктивне твердження зі стверджувальною інтонацією чи надаючи стверджувальної форми такому твердженню в разі письмового мовлення, суб'єкт мовлення подає його адресатові мовлення як фактично істинне. Якщо диз'юнктивне твердження позначене як істинне, то обидва твердження - складники цього твердження позначено як істинні або як такі, що мають протилежні значення істинності:

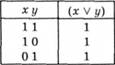
У такому разі можна сформувати такі три типи припущень:

1. Припущення про значення істинності одного з простих тверджень на підставі істинності складного твердження:

1) (х V у) > Од: (на тій підставі, що в мережі розрив або нема напруги (х V у), можна зробити припущення, що в мережі розрив (х)у тобто перше речення істинне);

2) (х V у) > 0 х (на тій підставі, що в мережі розрив або нема напруги (х V у), можна зробити припущення, що в мережі розриву нема (х), тобто перше речення хибне);

3) (х V у) > 0 у (на тій підставі, що в мережі розрив або нема напруги (х V у), можна зробити припущення, що нема напруги (у), тобто друге речення істинне);

4) (х V у) > 0 у (на тій підставі, що в мережі розрив або нема напруги (х V у), можна зробити припущення, що напруга є (у), тобто друге речення хибне).

2. Припущення про значення істинності одного з простих тверджень на підставі істинності складного твердження та знання значення істинності іншого простого твердження:

5) (х V у)у х > 0 у (на тій підставі, що в мережі розрив або нема напруги (х V у) та в мережі розрив (х), можна зробити припущення, що нема напруги (у), тобто друге речення істинне);

6) (х V і/), д: >0у (на тій підставі, що в мережі розрив або нема напруги (х V у) та в мережі розрив (х), можна зробити припущення, що напруга є (¿7), тобто друге речення хибне);

7) (х V у), у > Ох (на тій підставі, що в мережі розрив або нема напруги (д: V у) та нема напруги (у), можна зробити припущення, що є розрив (х), тобто перше речення істинне);

8) (х V у), у > 0 х (на тій підставі, що в мережі розрив або нема напруги (х V у) та нема напруги (у) можна зробити припущення, що розриву нема (л7), тобто перше речення хибне).

3. Припущення про значення істинності двох простих тверджень на підставі істинності складного твердження:

9) (х V у) > 0 (х /2 у) (на тій підставі, що в мережі розрив або нема напруги (х V у), можна зробити припущення, що в мережі розрив і нема напруги (х /8 у), тобто обидва речення істинні);

10) (х V у) (х /4 у) (на тій підставі, що в мережі розрив або нема напруги (х V у), можна зробити припущення, що в мережі розрив, але напруга наявна (х /4 у), тобто перше речення істинне, а друге - хибне);

11) (х V у) > 0 (х (2 у) (на тій підставі, що в мережі розрив або відсутня напруга (х V у), можна зробити припущення, що розриву нема, але відсутня напруга (х(2у), тобто перше речення хибне" а друге істинне).

На підставі змісту диз'юнкції (витлумаченого як позначення значень істинності тверджень) інших припущень, крім наведених вище, зробити не можна.

Щодо методів формування припущень можна стверджувати, що гіпотези наявні там, де є неповнота інформації, що можна тлумачити як неповноту засновків. Отже, для створення правил формулювання гіпотез потрібно:

1) виявити правила, необхідні для однозначного висновку;

2) вилучаючи як невідомі окремі частини засновків у цих правилах, отримати правила імовірнісних міркувань.