Менеджмент підприємства - Хомяков В.І. - ФОРМУЛЮВАННЯ ОБМЕЖЕНЬ

5.5.1. Загальні положення

Моделі лінійного програмування використовуються: а) при комерційних повітряних сполученнях для складання графіків польотів і графіків виходів льотного складу;

б) для оптимізації складових частин сумішей при розробці харчових раціонів;

в) дня оптимізації параметрів виробничих процесів у промисловості;

г) комерційними банками при управлінні фінансовими балансами;

д) при перспективному плануванні виробничих потужностей підприємства;

є) для оптимізації портфеля замовлень фірм при інвестуванні; ж) для оптимізації транспортних потоків.

З точки зору управління задачі лінійного програмування - це задачі оптимального використання ресурсів. В кожному випадку планування виробництва необхідно мати на увазі, що різні виробничі ресурси (робоча сила, сировина, матеріали, знаряддя виробництва) обмежені, відома норма витрат цих ресурсів на різні види продукції і можливі численні варіанти розподілу виробничих ресурсів. Завдання полягає в тому, щоб знайти оптимальний розподіл виробничих ресурсів. При цьому критеріями можуть бути, наприклад, максимум випуску продукції, максимум прибутку, мінімум виробничих витрат тощо.

5.5.2. Приклад розробки моделі лінійного програмування для виробництва двох виробів

Припустимо, що хімічний завод виробляє два види товарів - А і Б у кількості, відповідно рівній X і У. Менеджер, опрацювали відповідну інформацію, одержали дані, зведені в таблицю 5.9. Його метою є отримання максимального прибутку (Пр). При цьому цільова функція має вигляд:

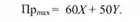
Таблиця 5.9. Вартісні показники товарів

ФОРМУЛЮВАННЯ ОБМЕЖЕНЬ

Робочий час обладнання при виробництві товарів характеризується такими цифрами:

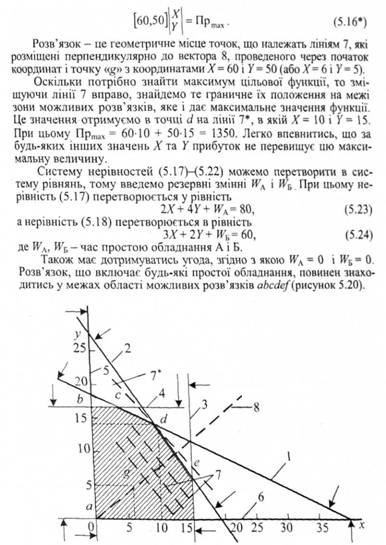
Рисунок 5.20. Графічний розв'язок лінійної оптимізаційної моделі (5.17) -(5.22)

Привабливість використання резервних змінних (у нашому випадку - це тривалість простоїв обладнання) можна продемонструвати на такому прикладі. Припустимо, що товару А вироблено 9 одиниць, а товару Б - 14 одиниць. Тоді, на основі рівняння (5.23) одержуємо, що

5.5.3. Транспортна задача

Вартість перевезень 1 т вантажу в гривнях із кожного пункту відправлення А1 та А2 в кожний пункт призначення В1, В2 та Вз задана у такому вигляді (цифри умовні):

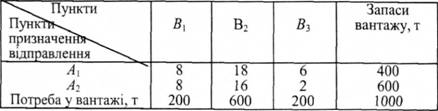
Потрібно скласти такий план перевезень, за якого загальна їх вартість була б найменшою.

Позначимо через Х1, Х2 та Х3 кількість вантажів, які потрібно перевезти з пункту А1, відповідно в пункти В1, В2 та В3, а через Y1, Y2 та Y3 - кількість вантажів, які потрібно перевезти з пункту А2 в пункти В1, В2 та В3. Запишемо це в такому вигляді:

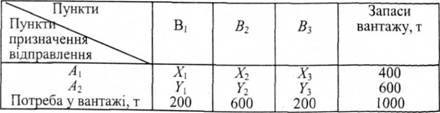
Таким чином, математичне формулювання транспортної задачі (за критерієм вартості транспортних перевезень) має вигляд даної системи п'яти рівнянь першого ступеня з шістьома невідомими:

ГЕОМЕТРИЧНЕ РОЗВ'ЯЗАННЯ ТРАНСПОРТНОЇ ЗАДАЧІ

Розглянемо систему (а). Якщо скласти почленно перші три рівняння і відняти четверте, то одержимо п'яте рівняння. Це означає, що в системі (а) п'яте рівняння зайве. Про таке рівняння кажуть, що воно - результат чотирьох рівнянь, а про всю систему кажуть, що вона лінійно залежна. Якщо виключити п'яте рівняння, то чотири рівняння, що залишилися, є лінійно незалежними. Таким чином, одержуємо чотири лінійно незалежні рівняння першого ступеня з шістьома невідомими. В цих рівняннях чотири невідомі можна виразити через два останні. У цьому випадку кажуть, що система має чотири залежні невідомі і два вільні невідомі. Оберемо вільними невідомими Х1 та Х2 і отримуємо:

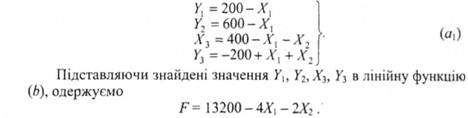
Серед розв'язків системи (а') потрібно знайти такий, за якого лінійна форма F набуває найменшого значення. Для розв'язання цієї задачі візьмемо на площині прямокутну систему координат і побудуємо багатокутник abсd можливих розв'язків системи нерівностей а' (рисунок 5.21). Запишемо цільову функцію у матричному вигляді:

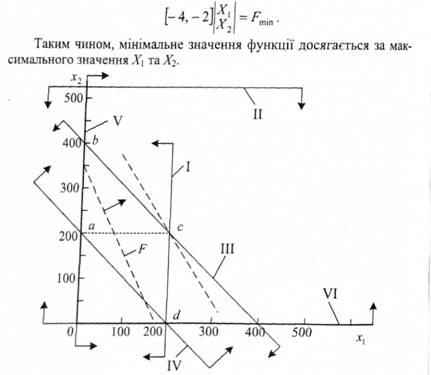
Рисунок 5.21. Графічне розв'язання транспортної задачі

На рисунку 5.21 цільова функція зображена штриховими лініями F. Значення функції зменшується зі збільшенням абсолютної величини вільного члена в рівнянні цільової функції. Змішуючи лінію цільової функції вправо паралельно до самої себе і віддаляючи її при цьому від початку координат, бачимо, що найменше значення вона має в точці перетину прямих (І) та (III). Це відповідає оптимальному розв'язку: Х1 = 200, Х2 = 200 (точка С). При цьому F = 12000. З рівнянь (а') знаходимо, що Х3 = 0, Y1 = 0, Y2 = 400, К3 = 200. Таким чином, оптимальним планом перевезення вантажів є такий: перевезти з пункту А1 по 200 т в В1 і в В2, а з пункту А2 400 т в В2 і 200 т в В3. Вартість перевезень при цьому найменша (12000 грн.).

Недоліком графічного (ручного) методу розв'язання моделі лінійного програмування є те, що він придатний для задач лише з двома або, максимум, з трьома змінними. Для більшої кількості змінних потрібно використовувати, так званий, симплекс-метод.