5.8.1. Загальна методика урахування фактора часу
Під фактором часу розуміють економічну нерівнозначність різночасних витрат і результатів. Якщо варіанти рішень відрізняються терміном здійснення, то для їх оцінки необхідно використовувати фактор часу, тому що некоректно порівнювати гроші в різні відрізки часу без їх приведення до якогось моменту. Цінність суми грошей у різні періоди часу залежить від ставки процента та відрізка часу. Процент, з точки зору торговельно-промислового підприємства або підприємця, може розглядатися як платіж за користування грошима.
Розглянемо найпростіші схеми приведення (дисконтування) різночасних витрат (результатів).


Рисунок 5.31. Графічне зображення еквівалентних один одному грошових потоків Н0 і F.
Графічне зображення еквівалентних початкового Н0 та кінцевого грошових потоків наведене на рисунку 5.31, а значення коефіцієнта (1 + е)-n - в таблиці 5.16.
Таблиця 5.16. Величина коефіцієнта (1 + е)-n для окремих платежів
n, років | Ставка процента e ,% | ||||
5 | 10 | 15 | 20 | ||
5 | 0,784 | 0,621 | 0,497 | 0,402 | |
10 | 0,614 | 0,386 | 0,247 | 0,162 | |
15 | 0,481 | 0,239 | 0,123 | 0,065 | |
20 | 0,377 | 0,149 | 0,061 | 0,026 | |
Варіант з однаковими щорічними платежами розглянемо на прикладах.

Графічно це ілюструється рисунком 5.32 а. Якщо кожну зі щорічних сум в 1000 грн. інвестувати за ставки процента 10%, у кінці четвертого року накопичується 4641 грн. Шляхом дисконтування отримуємо еквівалентну суму коштів, приведену до сучасного моменту
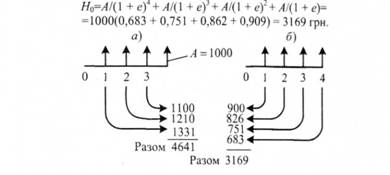
Рисунок 5.32. Приведення однакових щорічних грошових потоків до майбутнього (а) та сучасного (б) моментів

ФОРМУЛИ ЩОРІЧНИХ ПЛАТЕЖІВ


Таблиця 5.17. Значення коефіцієнта f
Рік | Ставка процента е, % | ||||
5 | 10 | 15 | 20 | ||
5 | 4,329 | 3,791 | 3,352 | 2,990 | |
10 | 7,722 | 6,144 | 5,019 | 4,192 | |
15 | 10,380 | 7,606 | 5,849 | 4,675 | |
20 | 12,462 | 8,514 | 6,259 | 4,870 | |
Приклад 5.6. Дехто планує піти у відставку через 10 років і шляхом щорічного збереження, накопичити за цей час 100000 грн. Гроші можуть бути вкладені за щорічної ставки 14%. Скільки потрібно відкладати щорічно?

Таблиця 5.18. Значення коефіцієнта щорічної амортизації
n, років | Ставка процента е,% | |||
5 | 10 | 15 | 20 | |
5 | 0,231 | 0,264 | 0,298 | 0,334 |
10 | 0,130 | 0,163 | 0,199 | 0,239 |
15 | 0,100 | 0,131 | 0,171 | 0,214 |
20 | 0,080 | 0,117 | 0,160 | 0,205 |
Приклад 5.7. Фірма позичила в банку 10000 грн. за річної ставки процента 10%. Цей кредит має бути погашений трьома однаковими щорічними платежами. Якими повинні бути ці платежі? Визначте кожний платіж на погашення суми боргу та процент.
Розв'язання. Щорічний платіж становить
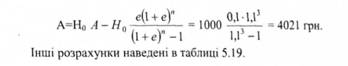
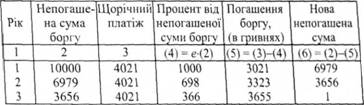
Таблиця 5.19. Розрахунки до прикладу 5.7
Приклад 5.8. а) Ви плануєте піти у відставку через 10 років і хочете до цього мати в банку суму, що дорівнює 100000 грн. Ставка процента залишається постійною і дорівнює 10% річних. Скільки грошей потрібно відкладати щорічно, щоб накопичити на кінець десятого року 100000 грн.? Припустимо, що гроші вкладаються однаковими частками в кінці кожного року.
б) Припустимо, що очікувана тривалість вашого життя після відставки дорівнює 10 рокам. Скільки грошей ви можете щорічно забирати з банку, щоб до кінця 20-го року (тобто десятого після вашої відставки) сума внеску зменшилась до нуля (тобто до очікуваного кінця вашого життя)? При цьому припустимо також, що щорічне вилучення здійснюється рівними частками в кінці кожного року.
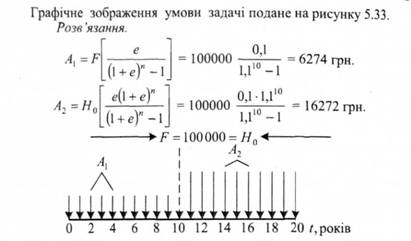
Рисунок 5.33. Графічне зображення умов прикладу 5.8
На рисунку 5.34 зображено інші можливі варіанти зведення рівномірно розподілених щорічних потоків до одномоментних у минулому або сучасному періодах часу.
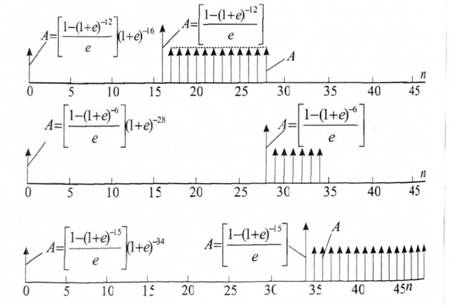
Рисунок 5.34. Варіанти приведення однакових щорічних грошових потоків до сконцентрованих потоків у минулому (сучасному) моменті часу

Рисунок 5.35. Зростання вартості грошових потоків в арифметичній (а) та геометричній (б) прогресії
В тому випадку, коли величина грошового потоку наступного періоду відрізняється від попереднього на постійний процент (див рисунок 5.35 6), величина потоку в кінці періоду визначається як:
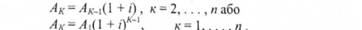
Приведена до початкового моменту (сучасного періоду часу)

УРАХУВАННЯ ІНФЛЯЦІЇ
Динамічна природа економіки в останні роки сфокусувала значну увагу на Інфляції та її впливі на прийняття рішень.
Альтернативні підходи, які звичайно враховують вплив інфляції, включають:
1) всі грошові потоки в поточних гривнях і комбінацію індексу інфляції (/) зі ставкою процента (є);
2) всі грошові потоки в постійних гривнях і використання ставки процента без урахування індексу інфляції.
Останній спосіб спеціалісти-практики вважають, за більш прийнятний. Однак нерідко при розрахунках використовується як ставка процента, так і інфляційний компонент.
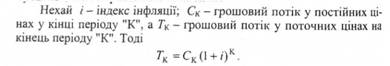
Грошові потоки в незмінних цінах можна розглядати як однорідний ряд, а в поточних цінах - як геометричний ряд.
Приведений до початкового моменту часу еквівалент грошових потоків визначається таким чином:
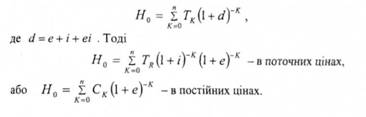
5.8.2. Методи та приклади прийняття рішень з урахуванням фактора часу
МЕТОД ПРИВЕДЕННЯ ВАРТОСТІ ДО СУЧАСНОГО МОМЕНТУ ЧАСУ
МЕТОД ВИЗНАЧЕННЯ ЩОРІЧНИХ ПРИВЕДЕНИХ ГРОШОВИХ ПОТОКІВ
ІНДЕКС ПРИБУТКОВОСТІ (ІП)
МЕТОД ОКУПНОСТІ ІНВЕСТИЦІЙ
МЕТОД ВИЗНАЧЕННЯ ВНУТРІШНЬОЇ СТАВКИ ДОХОДУ (ВСД)
МЕТОД ВИКОРИСТАННЯ ЗОВНІШНЬОЇ СТАВКИ ДОХОДУ (ЗСД)
ОЦІНКА ВАРІАНТІВ, ЩО НЕ ВКЛЮЧАЮТЬ ПОЗИТИВНІ ГРОШОВІ ПОТОКИ
РОЗВ'ЯЗАННЯ ЗАДАЧ З ВИКОРИСТАННЯМ ЗОВНІШНЬОЇ СТАВКИ ДОХОДУ