Важливим етапом прогнозування є верифікація прогнозів, тобто оцінювання їх точності та обґрунтованості. На етапі верифікації використовують сукупність критеріїв, способів і процедур" які дають можливість оцінити якість прогнозу.
Найбільш поширене ретроспективне оцінювання прогнозу, тобто оцінювання прогнозу для минулого часу.
Для цього вихідна інформація поділяється на дві частини, одна з яких охоплює більш ранні дані, а інша - більш пізні. За допомогою даних першої групи (ретроспекції) оцінюються параметри моделі прогнозу, а дані другої групи розглядаються як фактичні дані прогнозованого показника. Отримана ретроспективно помилка прогнозу певною мірою характеризує точність застосовуваної методики прогнозування.
Усі показники, що використовуються для аналізу якості прогнозу, можна розділити на три групи: абсолютні, порівняльні та якісні.
До абсолютних відносять показники, які дають змогу кількісно визначити величину помилки прогнозу в одиницях виміру прогнозованого об'єкта або у відсотках. Це середньоквадратична помилка а,, абсолютна помилка Апр, середня абсолютна помилка Д|ф, відносна помилка єпр та середня відносна помилка прогнозу єпр.
Абсолютна помилка прогнозу може бути визначена як різниця між фактичним значенням (у) і прогнозом (у*):
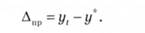
Середнє абсолютне значення помилки становитиме:
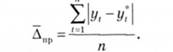
Середньоквадратична помилка прогнозу розраховується за формулою
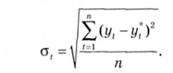
Слід зазначити, що для великого класу статистичних розподілів існує зв'язок середнього абсолютного відхилення Д|ір зі стандартним відхиленням а,, що можна представити в такому вигляді:
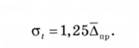
Недоліком розглянутих показників є те, що значення цих характеристик істотно залежить від масштабу виміру рівнів досліджуваних явищ.
Абсолютна помилка прогнозу Лпр може бути виражена у відсотках щодо фактичних значень показника в такий спосіб:
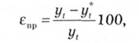
а середня відносна помилка (помилка апроксимації) розраховується як
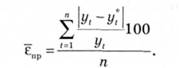
Цей показник, як правило, використовується при порівнянні точності прогнозів різнорідних об'єктів прогнозування. Типові значення єпр для середньострокових прогнозів та їх інтерпретації наведено в табл. 14.10.
Таблиця 14.10. Дані прогнозування та інтерпретації

Середня абсолютна і середньоквадратична помилки фіксують середнє значення помилки на кожному стані прогнозу без урахування цієї помилки. Середня помилка дає змогу визначити, який вид помилки є найбільш типовим - недооцінка чи переоцінка прогнозованого показника. Необхідно мати на увазі, що Лпр і о, дорівнюють нулю тільки тоді, коли у і - у* для кожного £, тобто у випадку досконалого прогнозу. Аналогічне твердження несправедливе для абсолютної помилки А , оскільки тут може мати місце взаємопогашення помилок. Для розрахунку цих показників можуть бути використані як абсолютні величини змінних, так і їхні прирости.
Порівняльні показники точності прогнозу ґрунтуються на порівнянні помилки розглянутого прогнозу з еталонними прогнозами певного виду.
Один із типів таких показників {К) може бути в загальному вигляді поданий так:
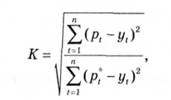
де р* - прогнозоване значення величини еталонного прогнозу.
Як еталонний прогноз може бути обрана проста екстраполяція, простий темп приросту і т. ін.
Окремим випадком показників такого типу є коефіцієнт невідповідності, у якому р* = 0 для всіх типів /:
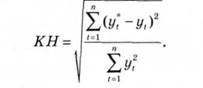
Можна побудувати різні модифікації коефіцієнта невідповідності. Розглянемо деякі з них.
1. Коефіцієнт невідповідності (КН^ обчислюється як відношення середньоквадратичної помилки прогнозу до тієї самої помилки, що мала б місце, якщо брати як прогноз для кожного року середнє значення змінної за весь період:
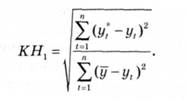
Якщо КН. > 1, то прогноз на рівні середнього значення дав би кращий результат, ніж отриманий прогноз.
2. Коефіцієнт розбіжності V становить відношення середньоквадратичної помилки прогнозу до тієї самої помилки, що мала б місце, якщо брати як прогноз для кожного року значення, вирівняне по аналітичному тренду, тобто
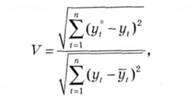
де у{ - екстраполююче значення досліджуваної величини на момент ї.
Якщо У> 1, то прогноз методом простої екстраполяції дає кращий результат.
До порівняльних показників варто віднести і коефіцієнт кореляції між прогнозованими і фактичними значеннями змінної Д:
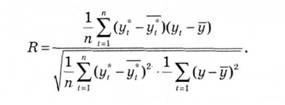
Одним із недоліків використання коефіцієнта кореляції як вимірника точності прогнозів є те, що повна позитивна кореляція лише вказує на наявність лінійної залежності між низкою прогнозних і фактичних величин. Унаслідок цього коефіцієнт кореляції найбільш придатний для аналізу прогнозів змінних, що циклічно розвиваються.
Якісні показники точності прогнозу дають змогу провести аналіз видів помилок прогнозу, поділити їх на складові. Особливо такий аналіз є важливий для змінних, що циклічно змінюються, коли необхідно прогнозувати не лише загальний напрямок розвитку, але і поворотні точки циклу.
Одним із методів такого аналізу є діаграма "прогноз - реалізація".
Сутність методу полягає в побудові точкових прогнозів у координатах, у яких на одній осі відкладається реальне значення змінної, на іншій її прогнозоване значення (рис. 14.10).
Використання діаграми дає змогу змістовно оцінити якість різних прогнозів, розрахувати коефіцієнти, що аналізують якість прогнозування поворотних точок, виділити найбільш
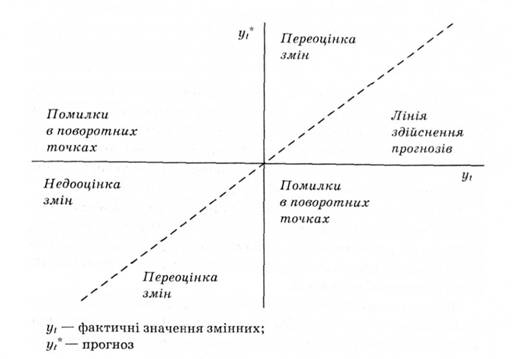
Рис. 14.10. Діаграма "прогноз - реалізація"
типові помилки (недооцінки або переоцінки змін). Для аналізу більш загальних видів помилок прогнозів може бути використана їх класифікація за джерелами виникнення.
Учений Г. Тейл поділив помилку прогнозу на частки невідповідності: частку зсуву (Т^ц), частку дисперсії (V ) і частку коваріації (Vі).
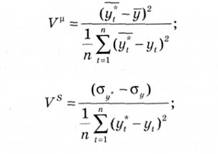
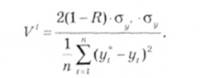
Чистка зсуву вказує на наявність помилки в оцінці центральної тенденції, тобто Vм* >0, коли середнє арифметичне значення прогнозів відрізняється від середнього арифметичного значення фактичних даних. На діаграмі "прогноз - реалізація" відсутність цієї помилки означає, що центр ваги точкових прогнозів лежить на лінії зроблених прогнозів.
Частка дисперсії відображає ступінь збігу стандартних відхилень прогнозу і фактичних значень. Vі =0 у тому випадку, коли а . = о.. Таким чином, цей показник відображає відповідності, ступеня нестійкості прогнозних значень ступеню нестійкості фактичної динаміки.
Частка коваріації і7'4 дорівнює нулю, коли коефіцієнт кореляції дорівнює одиниці між прогнозними і фактичними значеннями. На діаграмі "прогноз - реалізація" це відповідає випадку, коли всі точки лежать на одній прямій.
Усі розглянуті вище показники точності прогнозу використовуються при перевірці точності прогнозу, отриманого у вигляді точкових оцінок. Якщо при прогнозуванні отримано інтернальний прогноз, то мірою точності прогнозу можна вважати відносне число випадків до загального числа випадків, запропоноване професором Є.М. Четиркіним:
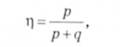
дер - число прогнозів, підтверджених фактичними даними;
9 - число прогнозів, не підтверджених фактичними даними.
Якщо п, = 1, то всі прогнози підтверджуються І Т) = 0, якщо вони не підтверджуються.
Розглянуті вище показники точності прогнозу можуть бути використані лише за наявності інформації про фактичні значення досліджуваного показника. Усі вони мають велику цінність при зіставленні різних методик прогнозування.
Якщо таких даних немає, то проблему точності можна розглядати як порівняння апріорних якостей і властивостей з притаманними альтернативним прогностичним моделям. Так, при прогнозуванні статистичними методами поняття апріорної точності прогнозу можна пов'язати з розміром довірчого інтервалу. У цьому випадку модель прогнозу вважається більш точною, якщо при одній і тій самій довірчій імовірності вона має вузький довірчий інтервал.
Вибір показників точності прогнозу залежить під за плані., які ставить перед собою дослідник при аналізі точності прогнозу. Про якість прогнозів, отриманих за різними методиками і моделями, можна судити лише за сукупністю зіставлень прогнозів та їх реалізації.