Концепції сучасного природознавства - Карпов Я. С. - 3.4.4 Ентропія та імовірність

В основі термодинаміки лежить відмінність між двома типами процесів — оборотними й необоротними.

Поняття ентропії дозволяє відрізняти у випадку ізольованих систем оборотні процеси (ентропія максимальна й постійна) від необоротних процесів (ентропія зростає).

Завдяки роботам великого австрійського фізика Людвіга Больцмана цю відмінність було зведено з макроскопічного рівня на мікроскопічний. Стан макроскопічного тіла (системи), заданий за допомогою макропараметрів (параметрів, що вимірюються за допомогою макроприладів — тиску, температури, об'єму й інших макроскопічних величин, які характеризують систему в цілому), називають макростаном.

Якщо стан макроскопічного тіла охарактеризовано настільки докладно, що задано стани всіх молекул, які утворюють тіло, то такий стан називається мікростаном.

Усякий макростан може бути зреалізованим різними способами, кожному з яких відповідає певний мікростан системи. Кількість різних мікростанів, що відповідають даному макростану, називається термодинамічною імовірністю макростану W. Спробуємо це з'ясувати.

Ми знаємо, що весь навколишній світ складається з молекул і атомів. Помістимо в якийсь резервуар із теплоізольованими стінками деяку кількість газу, число молекул якого дорівнює N. Виділимо яку-небудь одну молекулу. Припустимо, що якимось чином ми можемо її позначити, скажімо, пофарбувати в зелений колір. Якби ми могли це зробити, то одержали б можливість відрізнити її від інших молекул і тим самим спостерігати її рух у цьому об'ємі. Спостерігаючи за цією молекулою, ми вже незабаром переконаємося, що вона може перебувати в резервуарі де завгодно. Причому перебування її в будь-яку мить у будь-якій точці є випадковим.

Тепер поділимо наш об'єм на дві половини. Ми побачимо, що наша молекула, безладно блукаючи, постійно натикаючись (зіштовхуючись) на інші молекули, пробуде в одній з половинок резервуару рівно половину часу, протягом якого ми за нею спостерігаємо. У цьому випадку, як кажуть, імовірність ЇЇ перебування в одній з половинок резервуару дорівнює . Якщо ми будемо спостерігати вже за двома міченими молекулами, то імовірність того, що ми знайдемо відразу обидві молекули в одній з половинок посудини, дорівнюватиме добутку імовірностей кожної молекули 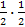.=.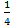 Аналогічно для трьох молекул ця імовірність дорівнює 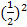, а для N молекул - 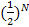. У 29 грамах повітря, наприклад, міститься кількість молекул N, що дорівнює 6,023 • 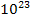. Відповідно, імовірність перебування відразу всіх молекул в одній половині об'єму посудини 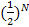мізерно мала. Така подія є малоймовірною. Нам це і не здається дивним. Дивним

було б, якби в одній кімнаті всі молекули повітря раптом у деякий момент часу зібралися б в одній її половині, а в іншій половині виявився б безповітряний простір. І якби ми не встигли або не здогадалися, що треба негайно перестрибнути в потрібну половину кімнати, то померли б від кисневого голодування. Ми знаємо, що така подія є малоймовірною. Імовірність же того, що всі молекули рівномірно розподілені по всьому об'єму у всьому об'ємі даної посудини, максимальна й приблизно дорівнює одиниці. Цей стан може реалізовуватися величезною кількістю способів. У цьому випадку термодинамічна імовірність, тобто кількість способів, якими може бути реалізований цей стан, максимальна.

Нехай у деякий момент часу нам вдалося загнати всі молекули за допомогою діафрагм (перегородок) у праву верхню частину посудини. Інші об'єму посудини залишалися при цьому порожніми. Далі заберемо діафрагми й побачимо, що молекули заповнять весь об'єм посудини, тобто перейдуть зі стану з меншою імовірністю у стан з більшою імовірністю. Тобто процеси в системі йдуть тільки в одному напрямку: від деякої структури (порядку, коли всі молекули містилися у верхньому правому кутку об'єму посудини) до повної симетрії (хаосу, безладдя, коли молекули можуть займати будь-які точки простору посудини).

Больцман першим побачив зв'язок між ентропією та імовірністю. При цьому він зрозумів, що ентропія повинна виражатися через логарифм імовірності. Тому що якщо ми розглянемо, скажімо, дві підсистеми однієї системи, кожна з яких описується термодинамічною імовірністю відповідно 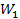і 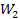, то повна термодинамічна імовірність системи дорівнює добутку термодинамічних імовірностей підсистем:

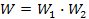
у той час як ентропія системи S дорівнює сумі ентропій підсистем:

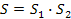
Зауважимо, що

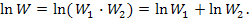
Больцман пов'язав поняття ентропії S з InW У 1906 році Макс Планк запропонував формулу, яка виражає основну думку Больцмана про інтерпретацію ентропії як логарифма імовірності стану системи:

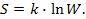
Планк виконав обчислення коефіцієнта пропорційності k — він збігся зі сталою Больцмана. Формула " 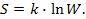" вигравірувана на пам'ятнику Больцману на цвинтарі у Відні.

Ідея Больцмана про ймовірну поведінку окремих молекул продемонструвала новий підхід до опису систем, що складаються з величезної кількості частинок, який уперше запропонував Максвелл. Максвелл прийшов до розуміння того, що в цих випадках фізична задача повинна бути поставлена інакше, ніж у механіці Ньютона. Очевидно, що наш приклад з міченими молекулами сам по собі нездійсненний, тому що, в принципі, неможливо простежити протягом значного інтервалу часу за рухом окремої молекули. Неможливо також визначити точно координати й швидкості всіх молекул макроскопічного тіла одночасно, в даний момент часу. Задачу слід сформулювати інакше, а саме: спробувати встановити ймовірність того, що дана молекула має певне значення швидкості. Максвелл увів для опису випадкового характеру поведінки молекул поняття імовірності, закон імовірності(статистичний). Використовуючи новий підхід, Максвелл сформулював закон розподілу кількості молекул газу по швидкостях. Цей закон викликав тривалу дискусію, яка тривала десятиліття аж до виготовлення молекулярних насосів, що дозволили зробити експериментальну перевірку закону. У1878 році Больцман, як уже було зазначено вище, застосував поняття ймовірності, уведене Максвеллом, і довів, що другий закон термодинаміки також є наслідком більш глибоких статистичних законів поведінки великої сукупності частинок. Таким чином, з розвитком статистичної фізики й термодинаміки на зміну причинним динамічним законам приходять статистичні закони, що дозволяють передбачити еволюцію природи не з абсолютною вірогідністю, а лише із значною часткою імовірності: