Загальна психологія - Скрипченко О.В. - 3.4.1. Упорядкування й рангування психологічних дослідних даних

Упорядкування дослідних даних полягає в такому.

1. Одержані дослідні дані слід класифікувати і згрупувати за якісними ознаками. Наприклад, при перевірці умінь і навичок читання необхідно проаналізувати дані про темп, способи, розуміння читання тощо.

2. Отримані показники якості слід упорядкувати. Наприклад, при перевірці у третіх класах темпу читання одержали від різних учнів такі дані: 119, 113, 123, 121, 128 тощо слід за хвилину. Цей ряд кількості слів треба впорядкувати так: 128,128,127,127,127 126,... 115,115,114, 114, 113,113, 110.

3. Необхідно згрупувати дані в таблицю (табл. 3.1).

Таблиця 3.1

Ця таблиця незручна для користування, оскільки дуже громіздка. Інтервал між даними - 18 рядів (128- 110= 18). У таких випадках для зручності вибирають інтервал не 1, а 1, 3,4 тощо.

4. Слід визначити величину інтервалу, користуючись формулою:

Складаємо таблицю.

Таблиця 3.2

5. Необхідно накреслити полігон частот у вигляді графіка розподілу частот. Полігон частот дає змогу наочно показати дослідні дані з психології.

Для закріплення матеріалу пропонуємо виконати таке завдання.

При оціненні міцності засвоєних знань перевірявся обсяг пам'яті. З цією метою кожному учневі читали один, ряд (цифр, букв, складів, слів тощо. Зрозуміло, що бралося щось одне), який поступово зростав.

Учні відтворювали ряд. Правильно було відтворено таку кількість слів: 4, 5, 5, 5, 4, 6,6... 7, 6, 9, 5, 3. Ці дані свідчать про те, що існують індивідуальні відмінності в обсязі пам'яті учнів (від 9 до 3). Складіть таблицю розподілу частот.

3.4.2. Визначення середніх при опрацюванні дослідних даних

У психологічних дослідженнях найчастіше визначають моду, медіану, середнє арифметичне, середнє квадратичне, квартілі тощо.

Не вдаючись у складні математичні формули, дамо вербальні визначення цих середніх.

1. Мода (Мо) - величина дослідної ознаки, яка найчастіше трапляється у сукупності. Наприклад: З, 3, 4, 5, 6, 6, 6, 6, 7, 7, 8, 9, 9, 10. Мо=6.

2. Медіана (Ме) є показником, який міститься в середині варіаційного ряду.

Наприклад: 3, 5,7,9, 11, 13,15. Ме = 9.

3. 5, 7,9, 11, 13, 15, 16.Ме = (9+1І):2 = 10. 3. Квартіль - наприклад, одержали ряд 2, 5,8,16,24,28, ЗО, 32.

Таблиця 3.3

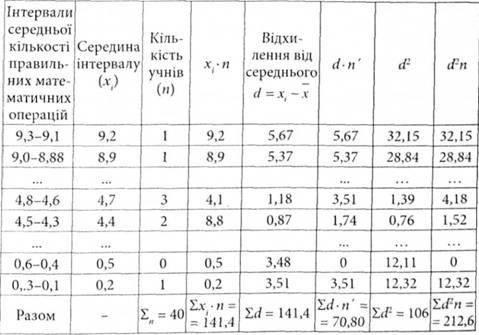
3.4.3. Використання міри дисперсії у психологічних дослідженнях

Окремі середні дані можуть мати ті самі середні арифметичні, але суттєво відрізнятись між собою.

Наприклад: 3,3,5, 7 і 1,3, 5,6, 7, 9 (в обох випадках х= 5).

Проте в першому варіанті дані варіюють у менш широких межах (від 3 до 7), ніж у другому (від 1 до 9), тобто їхня дисперсія (від лат. - розсіювання, розсипання), чи ступінь їхнього відхилення від x помітно більше розсіяний, дисперсійний.

Найуживанішими у психології є такі міри дисперсії:

1. Розмах - це інтервал між найбільшим і найменшим значенням у серії. Наприклад: З, 3, 5, 5, 8 - розмах 5 (8-3); 1, 3, 5, 7, 9, 1 - розмах 8 (9-1). Розмах є найзагальнішою й статистично малонадійною мірою дисперсії (розсіювання). Використовується для приблизного порівняння двох або декількох серій даних відносно міри дисперсії.

2. Середнє відхилення (МД).

3. Середнє відхилення й середнє квадратичне, або стандартне відхилення, характеризують зміни властивостей. Ці величини використовують у психології та педагогіці з різною метою, передусім для оцінення індивідуальних відхилень від середніх показників у засвоєнні знань, формуванні вмінь та навичок, у розумовому й моральному розвитку тощо. Розглянемо визначення цих величин на прикладах із життя школи.

Відомо, що вчителі, завучі, директори шкіл, інспектори тощо періодично перевіряють стан формування в учнів вмінь і навичок у виконанні математичних вправ. З цією метою складаються 2-4 варіанти рівнозначних вправ, ці вправи роздають кожному учневі так, щоб усі учні почали працювати одночасно (на звороті карток учні записують прізвище та ім'я, а потім за вказівкою вчителя перевертають картку і починають працювати). Виконавши завдання, учень піднімає руку, а той, хто перевіряє, записує час його роботи. При опрацюванні даних визначається кількість правильно виконаних математичних операцій за хвилину.

Середнє відхилення від середнього арифметичного визначається за формулою:

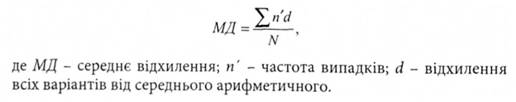
Якщо МД= 1,77 операцій за хвилину, то в цьому класі наявні індивідуальні відхилення, на які слід зважати вчителю. (МД визначається як середнє арифметичне відхилення, тому знаки "+" і "-" не беруться до уваги.

Такі розрахунки є недостатньо точними, тому за потреби в точному визначенні, наприклад, індивідуальних відхилень тощо, необхідно визначити середнє квадратичне, або стандартне відхилення. Воно визначається за формулою:

У випадках, коли можливе порівняння ступенів дисперсії двох серій досліджень, визначається коефіцієнт (сталий чи відомий множник при іншій невідомій або змінній величині) варіації (від лат. variatio -зміна, різновид; деяке відхилення від основного типу).

Порівнювати ступені дисперсії двох серій психологічних чи педагогічних досліджень можна за таких умов:

o якщо центральні тенденції (від нім. tendenz - напрямок розвитку якого-небудь явища) збігаються або приблизно однакові;

o якщо показники характеризують одну властивість (наприклад, навички читання, обсяг уваги тощо);

o якщо показники вимірюють в однакових одиницях.

Якщо ці умови порушуються, для порівняння двох серій досліджень необхідно вираховувати коефіцієнти варіації за формулами:

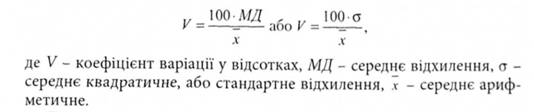
При опрацюванні дослідних даних вибірок важливо визначити, наскільки ймовірно, що дві вибірки належать до однієї популяції, тобто до загальної сукупності. У психологічних дослідженнях це важливо при визначенні одноманітних якостей у випадках їхнього розділення. або для встановлення, наприклад, ступеня впливу певних умов, методів навчання на його результати. В таких випадках беруть дані в контрольній групі і ті самі дані в експериментальній групі. За Стьюдентом, для опрацювання даних слід користуватись такою формулою:

Для визначення * слід звернутись до статистичних математичних таблиць, зокрема таблиці значимості критерію і Стьюдента. При цьому необхідно визначити кількість ступенів свободи.

Припустимо, якщо £ = 0,92, п = 30, то рівень ймовірності для 0,92 буде вищим за 0,05. Оскільки в таблиці 1,70, можемо говорити, що дві вибірки належать до однієї популяції. Коли мова йде про конкретний дослідний експеримент, то його умови суттєво не впливають на результати у межах значимості р 0,05. Вони значущі, коли г = 1,7 та більше.

Визначення коефіцієнта рангової кореляції у психологічних дослідженнях. Кореляційний аналіз застосовується при вивченні кореляції, тобто при з'ясуванні, чи існує який-небудь зв'язок між двома показниками в одні вибірці. Наприклад, між темпом читання і переключенням уваги чи між обсягом уваги та короткочасною пам'яттю тощо. Цей аналіз допомагає встановити, чи можна зробити висновок про значимість одного показника, знаючи величину другого показника (успіх у навчанні з математики і рівень розвитку операції узагальнення тощо). Коефіцієнти рангових кореляцій варіюють у межах від (+1) до (-1). (+1) показує прямий зв'язок між першою і другою парою, (-1) - зворотний зв'язок. У принципі тут багато залежить від кількості вибірок (кількості обстежуваних тощо). При психологічних дослідженнях з обмеженою кількістю обстежуваних звичайно вважається, що якщо коефіцієнт рангової кореляції становить 0,3, то можна вважати, що наявний певний несуттєвий взаємозв'язок, якщо 0,4-0,5 - то є середній або добре виражений зв'язок, якщо вище

0,61 - сильний взаємозв'язок, а якщо він перевищує 0,9, то коефіцієнт рангової кореляції є дуже сильним. Але ще раз застерігаємо, що при оцінці коефіцієнтів рангової кореляції слід ураховувати кількість вибірок. Є статистичні таблиці, за якими можна встановити значимість одержаних коефіцієнтів рангової кореляції.

Під час проведення психологічних досліджень використовують систему упорядкованих показників. Таких систем буває дві чи більше. Вони можуть бути взаємопов'язаними або ні, їхній зв'язок називають ранговою кореляцією, яка характеризується ступенем взаємозв'язку досліджуваних явищ. Наприклад, дослідник дав групі учнів два різних за змістом завдання й дістав два ряди, що характеризують час виконання цих завдань кожним учнем та бал, яким оцінюється якість їхнього виконання.

Якщо для кожної пари значень ранги (секунди, бали чи інші показники) повністю збігаються, то маємо максимально тісний позитивний зв'язок, який виражається числом (+1).

Якщо мінімальні ранги однієї змінної відповідають максимальним рангам другої (чи навпаки), то маємо максимально тісний негативний зв'язок, який виражається числом (-1). Якщо взаємозв'язку немає, дістають число 0. Для кількісного вираження тісноти й напрямку рангових змінних використовуються коефіцієнти рангової кореляції, які обчислюють за допомогою різних формул. Розглянемо їх.

1. Визначення коефіцієнта кореляції за схемою Браве-Пірсона (К. Пірсон (1857-1930) - розробив статистичний апарат, який використовується у психології та інших науках). Ці автори пропонують визначати коефіцієнт рангової кореляції (г) за такою схемою (табл. 3.4).

Таблиця 3.4

Коефіцієнт рангової кореляції обчислюється за формулою:

2. Визначення коефіцієнта рангової кореляції за Спірменом (Ч. Спірмен (1863-1945) - англійський психолог, розробив цикл статистичних методик з метою вимірювання структур інтелекту). Він обчислюється за формулою

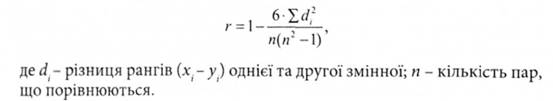
Наприклад, розглянемо взаємозв'язок між місцями учнів за кількістю розв'язаних задач першого й другого типу (табл. 3.5).

Таблиця 3.5

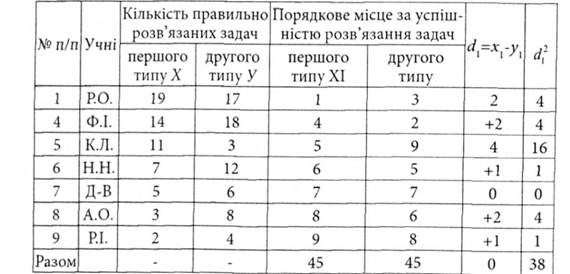
Підставивши значення з даних таблиці у формулу, дістанемо

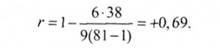
За схемою Спірмена зручно робити обчислення, коли порядкові місця в кожному ряді відповідно не збігаються, як у нашому прикладі.

3. Коефіцієнт рангової кореляції обчислюється і за допомогою формули

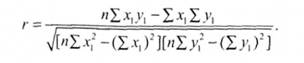
Ця формула використовується у тому разі, коли не треба визначати стандартних відхилень, а вихідні показники невеликі (див. табл. 3.6).

Таблиця 3.6

Підставимо значення у формулу й отримаємо

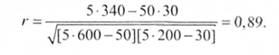
3. У тих випадках, коли поряд із коефіцієнтом рангової кореляції треба визначити середні квадратичні (стандартні) відхилення, а вихідні дані великі, слід використовувати формулу

3.4.4. Надійність і валідність

Тест чи інший метод має бути надійним. Під надійністю розуміють постійність, стабільність конкретної методики. Надійність є однією із важливих характеристик методів і психодіагностичних тестів, одним із критеріїв точності психологічних вимірів. Надійність відображує точність психологічного вимірювання і стійкість результатів.

Це означає, що повторне проведення того ж самого дослідження за тією ж самою методикою на тих самих обстежуваних має давати схожі результати чи оцінки.

Постійність оцінок при повторному експерименті за тією ж методикою з однією й тією самою групою людей називають ретестовою надійністю, постійність оцінок за пунктами тесту - внутрішньою погодженістю.

Стабільність методу оцінки кількісно визначається коефіцієнтом ретестової надійності. Цей коефіцієнт установлює кореляцію між результатами, одержаними на одних і тих самих обстежуваних у кожному з двох випадків проведення дослідження за однією і тією ж методикою. Теоретично цей коефіцієнт має становити (+1), але на практиці такий коефіцієнт малоймовірний. Надійною методику можна вважати, коли цей коефіцієнт буде в межах приблизно від (+0,70) до (+0,95). Поняття валідність близьке до поняття надійність, але їх слід диференціювати.

Валідність означає, що тест чи інша методика вимірює те, для визначення чого ця методика складена, створена. У психології виділяють такі види валідності:

1) змістова валідність - це ступінь відповідності змісту запитань тесту вимірюваній галузі психічних явищ;

2) конвергентна валідність - це величина кореляції показників одного тесту з показником іншого тесту, який, за гіпотезою, вимірює те саме психічне явище, що й перший тест (конвергенція - від лат. сходжусь, наближаюсь);

3) дивергентна валідність - це ступінь, у якому тест не вимірює те психічне явище, для оцінки котрого складався;

4) конструктивна валідність - це доказ того, що тест вимірює певний гіпотетичний конструкт, передбачає валідизацію як самого тесту, так і тих характеристик, які гіпотетично пов'язані з концепцією, що її дотримується експериментатор;

5) емпірична або практична солідність стосовно психодіагностичних методик означає відповідність результатів психодіагностики, проведеною за даною методикою, досвідом людини;

6) критеральна валідність пов'язана з обґрунтуванням кореляції мети результатами тесту і емпіричним критерієм;

7) прогностична валідність - це ступінь точності передбачення тестом деяких майбутніх критеріально-оріентовних вимірів;

8) поточна валідність - це ступінь кореляції тесту з незалежним виміром тієї ж самої змінної, одержаним у той самий час.

Наведені вище методи можна групувати за різними критеріями. Для прикладу візьмемо класифікацію Б.І. Ананьєва. Особливістю його класифікації є те, що вона бере за основу всі етапи дослідження. Так, першим етапом відповідає група організаційних методів. До них належить: порівняльний, лонгітюдний та комплексний методи.

Емпіричні методи, які поділяються на основні та додаткові: відповідають третьому етапу дослідження.

Методи статистичної обробки даних виконуються на четвертому етапі побудови психологічного дослідження. На п'ятому етапі дослідник використовує методи пояснення отриманих даних, якими можуть бути генетичний і структурний.