Психодіагностика - Галян І.М. - Оцінювання розподілу емпіричних даних

Для визначення способів математично-статистичного оброблення необхідно оцінити характер розподілу даних за всіма параметрами (ознаками). Для параметрів, що мають нормальний або близький до нормального розподіл, можна використовувати методи параметричної статистики, які часто є результативнішими, ніж методи непараметричної. Перевага їх полягає у можливості перевіряти статистичні гіпотези незалежно від форми розподілу.

Нормальний розподіл - вид розподілу змінних, що спостерігають при зміні ознаки (змінної) під впливом багатьох відносно незалежних факторів. Такий вплив характерний для психічних явищ, тому дослідник часто розраховує нормальний розподіл для статистичного опису сукупності емпіричних даних, оцінювання генеральної сукупності за вибіркою, для стандартного нормування тестових балів і переведення їх у шкальні оцінки. На властивостях нормального розподілу ґрунтуються статистичні критерії перевірки гіпотез (г-критерій, критерій х2" f-критерій Фішера, і-критерій Стьюдента тощо). Основною метою виявлення нормального розподілу є визначення методів математично-статистичного оброблення даних.

За нормального розподілу показників психологічної ознаки або наближеного до нього, що описує крива Гаусса, можна використовувати параметричні методи математичної статистики як найпростіші, надійні і достовірні: порівняльний аналіз, розрахунок достовірності відмінностей ознаки між вибірками за t-критерієм Стьюдента, f-критерієм Фішера, коефіцієнтом кореляції Пірсона тощо.

Якщо крива розподілу показників психологічної ознаки віддалена від нормальної, дослідник змушений використовувати методи не параметричної статистики: розрахунок достовірності відмінностей за критерієм Q Розенбаума (для малих вибірок), за U-критерієм Манна - Вітні, коефіцієнт рангової кореляції Спірмена, факторні, багатофакторні, кластерний та інші методи аналізу.

За характером розподілу можна отримати загальне уявлення про особливості вибірки досліджуваних за певною ознакою і валідність методики щодо вибірки.

Статистичні висновки, сформовані на основі моделі, наближеної до нормального розподілу, є теж приблизними. Оцінювання наближення практичної кривої до параметрів нормалі здійснюється шляхом розрахунку коефіцієнтів асиметрії, ексцесу і критеріїв погодженості Пірсона, Колмогорова і Ястремського.

Коефіцієнт асиметрії Аs оцінює розміщення вершини практичної кривої щодо теоретичної, показує величину зсуву вершини щодо розрахункової вершини по горизонталі (вправо "+"; уліво "-") (рис. 2.3).

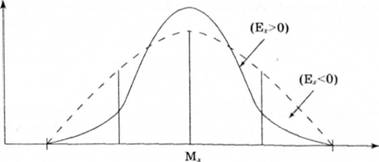
Рис. 2.3. Соціометричний розподіл емпіричних даних

Коефіцієнт асиметрії - показник скошеності розподілу в лівий або правий бік по осі абсцис на рис. 2.4.

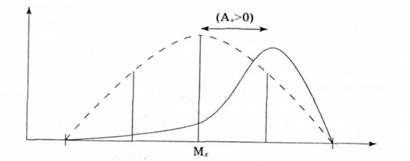
Рис. 2.4. Асиметричний розподіл емпіричних даних

Якщо права гілка кривої довша за ліву, йдеться про правосторонню (позитивну) асиметрію, а якщо ліва гілка довшу за праву - про лівосторонню (негативну) асиметрію (рис. 2.5).

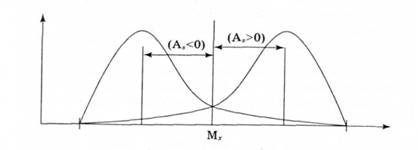
Рис. 2.5. Бімодальний розподіл емпіричних даних (право - та лівостороння асиметрія)

Коефіцієнт асиметрії Аs розраховують за такою формулою:

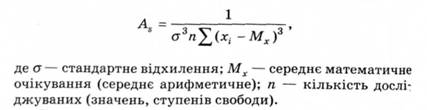
Коефіцієнт ексцесу Ех, тобто певних "ділянок" (груп частот) практичної кривої щодо теоретичної нормалі, визначає зсув практичної кривої (вершини) (по вертикалі - нагору "+"; униз "-"). Ексцес є показником гостроверхості. Криві, вищі у середній частині (гостроверхі) називають ексцесивними. При зменшенні величини ексцесу крива стає плоскішою, набуваючи вигляду плато, а потім і сідлоподібною, тобто з прогинанням у середній частині (рис. 2.6).

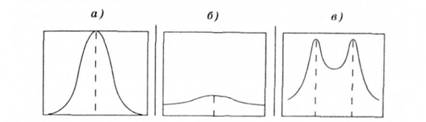
Рис. 2.6. Показники ексцесивності розподілу

Ці параметри допомагають отримати перше наближене уявлення про характер розподілу:

- у нормальному розподілі рідко можна знайти коефіцієнт асиметрії, наближений до одиниці і більший за неї (-1 і +1);

- ексцес ознак з нормальним розподілом зазвичай має величину в діапазоні 2-4.

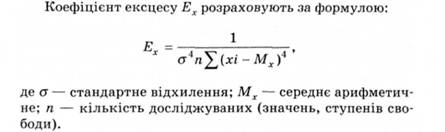
У простішому варіанті показники асиметрії і ексцесу з їх помилками репрезентативності визначають за такими формулами:

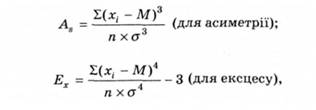
Обчислити показники асиметрії і ексцесу емпіричного розподілу можна, використовуючи функцію "Описова статистика" у програмі Excel.

Показники асиметрії і ексцесу свідчать про достовірну відмінність емпіричних розподілів від нормального у тому разі, якщо вони перевищують за абсолютною величиною свою помилку репрезентативності у 3 і більше разів:

Загальною причиною відхилення форми вибіркового розподілу ознаки від нормального вигляду найчастіше є особливість процедури вимірювання: шкала, яку використовують, може мати нерівномірну чутливість до властивості, що вимірюють, у різних частинах діапазону мінливості.

Такі емпіричні відхилення від нормального вигляду, як право - або лівостороння асиметрія чи незначний ексцес (або бімодальний розподіл) часто спостерігаються на практиці. Пов'язано це з особливостями експериментальної вибірки і вимірювальними процедурами, що застосовують.

Методи статистичного аналізу емпіричних даних допускають відхилення від нормального розподілу (одні - більшою мірою, інші - меншою). Однак якщо потрібне переконливе обґрунтування отриманих результатів і зроблених на їх основі обчислень, як додаткові слід використовувати нескладні методи неп ара метричної статистики.

Крива розподілу тестових балів Гауса у характеристиці психологічних явищ (оцінок, результатів виконання завдань тощо) відображає властивості пунктів, з яких складений тест (завдання), а також характеризує склад вибірки досліджуваних (наскільки успішно вони виконують завдання, наскільки тест чи завдання диференціюють вибірку за відповідною якістю, ознакою).

Якщо крива має правосторонню асиметрію, це означає, що в тесті переважають важкі завдання (для вказаної вибірки); якщо крива має лівосторонню асиметрію, це свідчить, що більшість пунктів у тесті легкі. Це може бути зумовлене такими причинами:

- тест (завдання) погано диференціює досліджуваних з низьким рівнем розвитку здібностей (властивостей, якостей, характеристик): більшість досліджуваних одержують приблизно однаковий низький бал;

- тест погано диференціює досліджуваних з високим розвитком здібностей (властивостей, якостей, характеристик): більшість досліджуваних одержують високий бал.

Аналіз ексцесу кривої розподілу дає змогу зробити такі висновки залежно від форми розподілу показників (даних, варіант) психологічної ознаки:

1) коли виникає значний позитивний ексцес (ексцесив - на крива) і бали концентруються поблизу середнього значення (мал. 2.6, а), це можуть зумовлювати такі причини:

- ключ складений неправильно, тобто при підрахунку з'єднані негативно пов'язані ознаки, які взаємно нейтралізують бали. Використання валідних і надійних методик унеможливлює виникнення такої проблеми;

- досліджувані застосовують, розгадавши спрямованість тесту (опитувальника), спеціальну тактику "медіанного бала": штучно балансують відповіді "за" і "проти" щодо одного з полюсів психологічної ознаки, яка вимірюється;

2) за підбору пунктів, що тісно позитивно корелюють між собою (тобто випробування не є статистично незалежними), в розподілі балів виникає негативний ексцес, що набуває форми плато (мал. 2.6, б);

3) негативний ексцес досягає максимальних величин зі збільшенням увігнутості вершини розподілу аж до утворення двох вершин - двох мод (з прогином між ними, мал. 2.6, в). Така бімодальна конфігурація розподілу балів указує на те, що вибірка досліджуваних розділилася на дві категорії, підгрупи (з плавним переходом між ними): одні справилися з більшістю завдань (погодилися з більшістю питань), інші - не справилися (не погодилися). Розподіл свідчить, що в основі завдань (пунктів) є одна спільна для всіх ознака, яка відповідає певній властивості досліджуваних: якщо у досліджуваних наявна ця властивість (здатність, знання, уміння), то вони справляються з більшістю пунктів, завдань, а за відсутності її - не справляються.

Первинні статистики чутливі до наявності варіант, що випадають. Великі величини ексцесу і асиметрії часто е індикатором помилок при підрахунках вручну або при введенні даних через клавіатуру для комп'ютерного оброблення. Грубі помилки при введенні даних можна знайти, порівнявши величини сигм в аналогічних параметрах. Сигма може вказувати на помилки.

При цьому дотримуються правила, за яким всі дії слід виконувати двічі (особливо відповідальні - тричі), бажано різними способами, з варіацією послідовності звернення до числового масиву.

Великі показники ексцесу і асиметрії можуть бути спричинені недостатньою надійністю і валідністю методик.

У окремій вибірці не можна повністю охарактеризувати ціле (генеральну сукупність, популяцію), завжди є ймовірність недостатньо точної, навіть помилкової оцінки генеральної сукупності на основі вибіркових даних. Помилки, узагальнення, екстраполяції, пов'язані з перенесенням результатів, отриманих при вивченні вибірки, на всю генеральну сукупність, їх називають помилками репрезентативності.

Репрезентативність - ступінь відповідності вибіркових показників генеральним параметрам.

Статистичні помилки репрезентативності показують, в яких межах можуть відхилятися від параметрів генеральної сукупності (від математичного очікування або істинних значень) часткові результати, отримані на основі конкретних вибірок. Величина помилки тим більша, чим більше варіювання ознаки і чим менша вибірка. Це відображають формули для обчислення статистичних помилок, що характеризують варіювання вибіркових показників навколо їх генеральних параметрів. Тому до первинних статистик обов'язково зараховують статистичну помилку середнього арифметичного. її обчислюють за формулою:

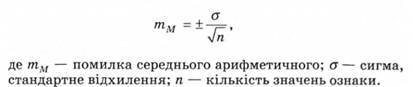
Основні методи параметричної і непараметричної статистики дають змогу обґрунтувати результати емпіричного психологічного дослідження.