Математична статистика - Руденко В.М. - Квантилі

Квантилем називається значення ранжированої змінної, що відокремлює від варіаційного ряду певну частку обсягу сукупності. Квантиль - загальне поняття. В математичній статистиці використовуються такі квантилі:

o процентилі (Р₁, Р₂, ..., Р99);

o децилі (П₁, П₂, ... ,

o квінтилі (К₁, К₂, К₃, К₄);

o кварталі 62, 6з).

Найбільш поширеними є процентилі (персентилі) і квартилі.

Процентилі ділять упорядковану сукупність на сто частин, тобто відокремлюють від сукупності по 0,01 частині (по 1%).

Квартилі ділять сукупність на чотири частини. Перший квартиль £)₁ відокремлює зліва 0,25 обсягу сукупності. Другий квартиль £)₂ ділить сукупність на дві рівні за обсягом частини (по 0,5), він називається медіаною. Нарешті, третій квартиль £)₃ відокремлює зліва 0,75 обсягу сукупності.

Між різними квантилями існують певні співвідношення, наприклад, між квартилями і процентилями такі: Р₂₅, <2₂= Р₅₀, <2₃= Р₇₅. Тому досить знати лише процедуру знаходження, наприклад, процентилей, щоб визначити будь-які потрібні квантилі. Знаходження персентилей є найбільш простим. Перед початком обчислення будь-якого процентиля слід упорядкувати дані за збільшенням. Р-Й процентиль є межа, нижче за яку лежать Р відсотків значень. Обчислювати квантилі можна графічно або за таблицями. Так з рис. 2.47 видно, що 25-й процентиль Р₂₅ і 1-й квартиль £)₁ дорівнюють значенню 3 (Р₂₅=3 і 6₁=3) Отже, нижче за це значення знаходяться 25% усіх значень. Аналогічно можна знайти інші співвідношення, наприклад Р₇₅ і £)₃ (75-й процентиль і 3-й квартиль) дорівнюють 6. Нижче за це значення знаходяться 75% всіх значень.

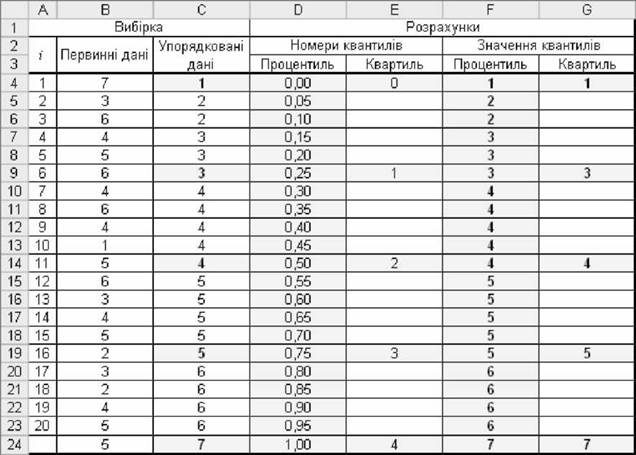
Рис. 2.47. Співвідношення квантилів

Для великих обсягів зручніше користуватися функціями MS Excel =ПЕРСЕНТИЛЬ() і =КВАРТИЛЬ(). На рис. 2.47 у комірки F4 і G4 внесено =ПЕРСЕНТИЛЬ($С$4:$С$23;04) і =KBAPTHJTb($C$4:$C$23;E4) відповідно.

Функція =ПЕРСЕНТИЛЬ(.мй^,сив; k) повертає k-ий процентиль для значень із масиву даних (значення k задається в інтервалі від 0 до 1 включно). Цю функцію можна використовувати для визначення межі прийнятності, наприклад, зараховувати курс навчальної дисципліни тільки тим студентам, які набрали балів не менш, ніж 75-й процентить. Якщо k не є кратним 1/(п - 1), то функція =ПЕРСЕНТИЛЬ() виконує інтерполяцію до k-oro процентиля. Для характеристик розподілів використовують квартилі. Функція MS Excel =КВАРТИЛЬ(масив; k) повертає відповідне до табл. 2.3 значення квартиля.

Таблиця 2.3

Значення функції =KBAPTHJIbOMS Excel

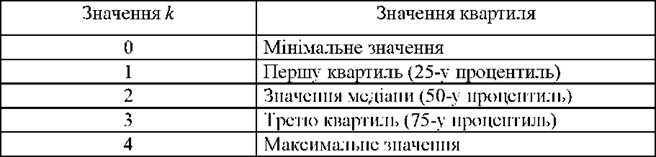
Через квартилі можуть визначатися числові характеристики центральної тенденції, мінливості. Наприклад, середнє квартильне відхилення - це міра розкиду в розподілах, яка параметром центральної тенденції має медіану Мо'.

"Чутливою" мірою розсіяння є напівінтерквартильне відхилення Е. Воно визначається як половина інтервалу, якому відповідає половина обсягу у сукупності, тобто Е = 0,5-(2₃ - де £)₃ і £)₁ - 3-й і 1-й квартилі.

Нормовані дані

Нормовані дані - це дані, наприклад, масиву X (див. рис. 2.48), що отримані шляхом математичного перетворення їх за формулою

х. -X

*> , (2.21)

де ху - значенняу'-го елемента первинного масиву даних X;

X і я_х - середнє арифметичне і стандартне відхилення масиву Х₁;

2у - нормоване значення.

Так, нормоване значення1-го елемента 2₁ дорівнюватиме (рис. 2.48):

21 = *^ - ь³⁷⁹ ,-1,71 ¹ Ух 1,63 ¹

Нормовані дані можна отримати у такій послідовності:

o для емпіричних даних (стовпчики А:В рис. 2.48) розрахувати значення

середнього X і стандартного відхилення я_х у рядках 16 і 17 за допомогою

функцій =СРЗНАЧ() і =СТАНДОТКЛОН();

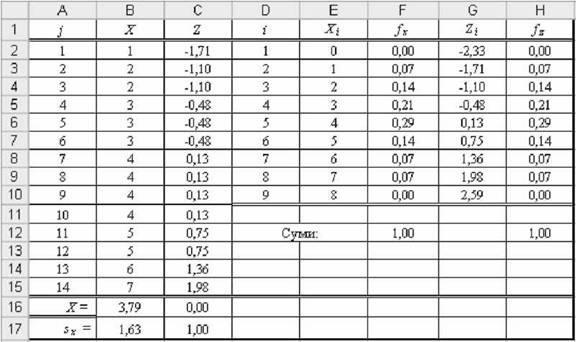
Рис. 2.48. Результати розрахунку стандартизованих значень 2

o у комірку С2 внести вираз =(В2-$В$16)/$В$17 і отримати відповідне нормоване значення -1,71;

o аналогічні вирази внести у комірку С3:С15 (рис. 2.49);

o розрахувати у комірку С16 і С17 середні значення і стандартні відхилення нормованих змінних 2 і переконатися, що вони становлять 0 і 1;

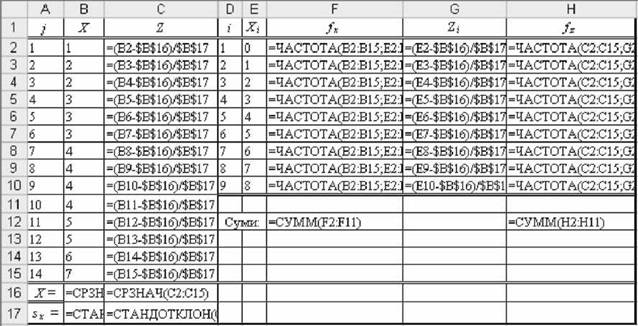
Рис. 2.49. Формули для розрахунку стандартизованих значень 2

o розрахувати у стовпчиках 0:И розподіли частот £ первинних і £ нор-

мованих даних з використанням функції =ЧАСТОТА() (див. рис. 2.48 - 2.49) і побудувати відповідні графіки (див. рис. 2.50 ).

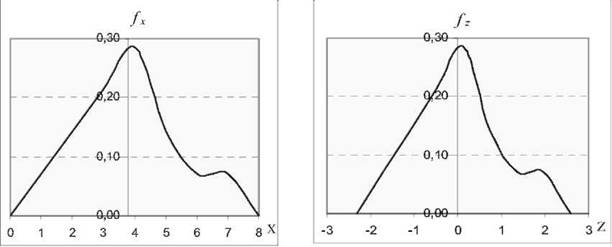
(а) (б)

Рис. 2.50. Графіки розподілу даних: а) первинних; б) стандартизованих

З рис. 2.50 можна переконатися, що графіки варіаційних розподілів первинних і нормованих даних ідентичні за формою, осі ординат проходять по значенням середніх: для первинних це значення складає 3,79, для нормованих - 0,00. Різними є і показники середньоквадратичного відхилення - 1,63 і 1,00 відповідно. Метод нормалізації доволі часто використовується в статистичних методах (див., наприклад, розділ 2.3).

Запитання. Завдання.

1. Дайте визначення і охарактеризуйте особливості показників МЦТ.

2. Як розрахувати моду, медіану і середнє арифметичне вибірки.

3. Поясніть поняття "унімодальність" і "бімодальність" розподілу.

4. Як визначити середнє арифметичне, якщо дані представлено розподілами частот?

5. Охарактеризуйте вибіркову дисперсію і стандартне відхилення, запишіть розрахункові формули.

6. Які властивості характеризують показники асиметрії і ексцесу?

7. Що таке початкові та центральні моменти?

8. Які показники вибірки можна визначати за допомогою моментів?

9. Що таке "квантиль", які квантилі застосовує математична статистика?

10. Яке співвідношення існує між квартилями і процентилями?

11. Що означає поняття "нормовані дані", яка формула перетворення?

12. Виконайте математичні процедури завдань за трьома способами розрахунку показників МЦТ і ММ в MS Excel.

13. Виконайте лабораторну роботу № 3.