Математична статистика - Руденко В.М. - Ймовірність подій

Випадкову подію можна передбачити лише з деякою ймовірністю.

Ймовірність події - це чисельна міра об'єктивної можливості цієї події (інтуїтивне означення ймовірності). Ймовірність події А позначається Р(А). Якщо здійснювати різноманітні випробування, то можна констатувати, що різні випадкові події можуть мати різну можливість появи.

Ймовірність неможливої події и дорівнює нулю, Р(Ц) = 0.

Ймовірність достовірної події V дорівнює одиниці, Р(У) = 1.

Отже, ймовірність Р(А) будь-якої випадкової події А знаходиться між нулем і одиницею: 0<Р(А) <1.

Інколи події можна вважати рівноможливими, якщо за умовами випробувань відсутні підстави вважати деякі з них більш можливими, аніж будь-які інші. Якщо декілька подій: 1) утворюють повну групу; 2) несумісні; 3) рі-вноможливі, то вони мають назву "випадки".

Класична ймовірність події А - це число Р(А), до якого наближається відношення кількості появлень бажаної події А до загальної кількості можливих подій вибіркового простору при збільшенні незалежно виконаних випробовувань:

_ кількість _ появлень _ бажаної _ події _ А

^{Р(А) =} : : ттт^{-. (3.1)}

загальна _ кількість _ можливих _ подій

Якщо результати досліду зводяться до схеми випадків, то ймовірність події А обчислюється як відносна частота здійснення події А:

Р( А) = ^т, (3.2)

п

де т - кількість появлень бажаних випадків або сприятливих подій; п - загальна кількість випадків.

Отже, для випадкової вибірки обсягом п відносні частоти /Цх₁)=т_і/п можна трактувати як ймовірності р(х) появи значень варіант х,-.

Приклад 3.2. Знайти чисельне значення ймовірності Р(А) події А, що студент на іспитах з 20 рівноможливих білетів (це загальна кількість випадків) витягне з першого разу білет №7 (бажаний вибірковий об'єкт).

Рішення: Кількість появлень бажаних подій m=1, загальна кількість випадків n=20. Значення ймовірності Р(А) події А - це відношення m / n:

P( A) = ^m = - = 0,05 = 5%. n 20

Відповідь: ймовірність витягти з першого разу білет №7 складає 0,05 або 5%.

Приклад 3.3. Студент знає відповідь лише на 5 екзаменаційних білетів і не знає відповіді на решту 15 білетів. Яка ймовірність того, що перший витягнутий навмання білет виявиться таким, на який студент знає відповіді?

Рішення: Загальна кількість білетів складає 5+15=20 (n=20), сприятливих для студента результатів всього 5 (m=5). Звідси ймовірність бажаної події:

P( A) = ^m = - = 0,25 = 25% n 20

Відповідь: ймовірність витягти бажаний білет складає 0,25 або 25%.

Отже, ймовірність події є основним поняттям теорії ймовірності, проте розглянуті класичні означення ймовірностей, а також наведені приклади дають лише загальне інтуїтивне уявлення щодо оцінки та прогнозування ймовірності. Ці методологічні підходи не дають строгих чисельних значень. Не всі події можна вважати рівноможливими, не всі ймовірності можна оцінювати як збіжності частот, неясно і те, скільки випробовувань треба здійснювати та ін.

Розглянемо означення ймовірності у рамках аксіоматичного підходу до математичної моделі, що була запропонована A.M. Колмогоровим.

Означення. Ймовірність. Нехай скінчена множина Q={co} є простором елементарних подій ю, що відповідають деякому стохастичному⁹ дослідові. Нехай кожній елементарній події ю, яка належить до множині Q, тобто йєП, поставлено у відповідність невід'ємне число Р(со), тобто Р(со)>0. Число Р(со) означимо як імовірність елементарної події ю, причому сума ймовірностей всіх елементарних подій дорівнює 1, тобто:

£ РИ = 1. (3.3)

weq

Пара {Q, Р} є імовірнісним простором, який складається зі скінченої ⁹ Стохастичний (від грец. stochastikos - спроможний угадувати), випадковий, імовірнісний.

множини О і невід'ємної функції Р, яка визначена на множині О і задовольняє умові (3.3). Звідси ймовірність Р(А) деякої події А дорівнює сумі ймовірностей елементарних подій ю, що входять до події А:

Р( А) =Е РИ. (3.4)

Тоді будь-яку числову функцію Р(А), визначену на скінченій множині Сі={ю}, яка є простором елементарних подій ю, називають імовірністю, якщо виконуються три умови (аксіоми Колмогорова):

1) Р(А) >0 для будь-якої А є О.;

2) ДП)=1;

3) Р(А₁ уА₂иА₃ и...) = Р(А₂)+ Р(А₃)+... для попарно несумісних випадкових подій (А_ір| А_х = 0, і Ф _)).

Отже, сконструйовано математичний об'єкт, який можна застосовувати при побудові імовірнісних моделей. Наприклад, випробуванням з підкиданням монети відповідає імовірнісний простір {Сі, Р}, де О = {ГД,} - множина елементарних подій; Р(Г) = Р(Ц) = 4 - ймовірності елементарних подій; позначення елементарних подій: Г - "випав герб", Ц - "випала цифра".

Аксіоматичне означення ймовірності Р(А) погодиться з інтуїтивним, згідно з яким ймовірність події А - це число від 0 до 1, що є збігом частоти реалізації події А при необмеженому числі повторень і постійних умовах випробувань.

З визначення імовірності події, а також умов (3.3) і (3.4) випливають інші властивості ймовірностей:

4) Для будь-якої події А ймовірність протилежної події Р(А) = 1 - Р(А).

5) Сума ймовірностей протилежних подій дорівнює одиниці:

Р( А) + Р( А) = 1.

6) Ймовірність достовірної події Р(СІ) = 1 (за аксіомою 2).

7) Ймовірність неможливої події Р(О.) = 1 - Р(С£) = 1 - 1 = 0.

8) Ймовірність добутку АР сумісних подій А і В: Р(А ■ В) = Р(А) ■ Р(Б). З діаграми рис. 3.2а видно, що сумісні події А і Б мають загальну (сумісну) площу подій (зафарбована площа), тому ймовірність добутку сумісних подій Р(АР )> 0.

9) Ймовірність суми А+В сумісних подій А і В визначається формулою: Р(А + В) = Р(А) + Р(В)-Р(А■ В), де Р(А■ В)- ймовірність добутку подій А і В. З діаграми рис. 3.26 видно, що події А і В мають сумісну площу подій, яка менша за суму окремо взятих подій А і В на величину добутку АР подій А і В. Відповідно ймовірність суми сумісних подій Р(В+С) < Р(В)+ Р(С ).

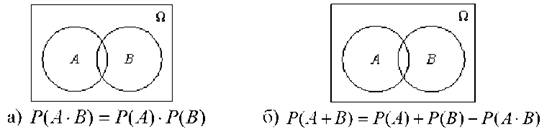
Рис. 3.2. Ймовірності добутку і суми сумісних подій А і В

10) Ймовірність добутку АР несумісних подій А і В дорівнює нулю. З діаграми рис. 3.3а видно, що несумісні події А і В не мають спільної площі, перетин відповідних підмножин є порожня множина 0 подій, тому ймовірність добутку несумісних подій Р(АР) = 0.

11) Ймовірність суми А+В несумісних подій А і В визначається спрощеною формулою: Р(А+&) = Р(А) + Р(В). З діаграми рис. 3.36 видно, що події А і В не мають спільної площі подій, яка б зменшувала загальну суму окремо взятих подій В і С.

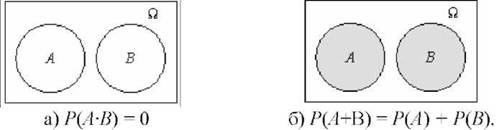
Рис. 3.3. Ймовірності добутку і суми несумісних подій А і В

12) Сума ймовірностей всіх несумісних подій {А₁, ^4₂, А_п}, що утворюють повну групу, дорівнює одиниці

Р(АЛ + Р(А₂) +, + Р(Ап) = 1 або £Р(А) = 1.

При застосуванні методів теорії ймовірностей і математичної статистики використовується поняття незалежності подій. Події А, В, С, ... є незалежними, якщо ймовірність їхнього спільного здійснення дорівнює добуткові ймовірностей здійснення кожної з них окремо: Р(АР^С) = Р(А)-Р(ВуР(С)... .

Згідно з цим означенням здійснення або нездійснення однієї незалежної події не повинне впливати на здійснення або нездійснення іншої. Наприклад, у випробуваннях при незалежному підкиданні двох монет простір елементарних подій складається з чотирьох елементів: ГГ, ГЦ, ЦГ, ЦЦ (позначення елементарних подій: ГГ - для першої монети випав герб і для другої - теж герб; ЦГ - для першої - цифра, для другої - герб і т.д.). Оскільки події типу "Г - для першої монети випав герб" і "Г - для другої монети випав герб" є незалежними за визначенням незалежних випробувань, і ймовірність кожного з них дорівнює 4, то ймовірність події ГГ дорівнює 4 - 4 = А. Аналогічно ймовірність кожного з інших елементарних подій також дорівнює А. Звідси сума ймовірностей всіх чотирьох елементарних подій дорівнюватиме одиниці.