Математична статистика - Руденко В.М. - Центральна гранична теорема

Розглянемо два варіанта центральної граничної теореми.

1. Центральна гранична теорема для однаково розподілених доданків -теорема Ліндеберга-Леві.

Для незалежних однаково розподілених випадкових величин X₁, X2, X,, з математичними сподіваннями МРУ;] = Ц і дисперсіями D[X₁] = а² (і = 1, 2,

¹⁷ Визначена оцінка іноді є заниженою, наприклад, для нормального розподілу вона складає біля 0,997 (за так званим закон трьох сигм, див. розділ 3.4).

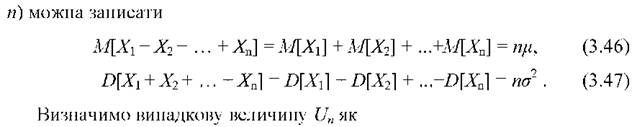
_{U =} X1 + X2 + ...+Xn -M[X 1-M[X2-...-M[Xn ⁿ ,/D[ X 1 + D[ X, + ... + D[ Xn '

З урахування виразів (3.46) і (3.47) випадкова величина U_n виглядатиме як

U_n = ^{X1 + X2 +} >^{+ Xn} ~ⁿ" . (3.48)

cw n

Для величини U_n математичне сподівання M[U_n = 0, дисперсія D[U_n = 1. Тоді при n-*" для будь-якого числа х існує границя

lim РІ ^{X1 + X 2 +} >^{+ Xn} ~ < x) = Ф( x), (3.49)

де Ф(х) - функція стандартного нормального розподілу

x

ф( x) = cp(t)dt, (3.50)

де <^(t) - щільність стандартного нормального розподілу

1 -

cp(t) = -=e ². (3.51)

V27t

n _

Якщо враховувати, що X₁ + X₂ +... + X_n = ^X_i = nX, то змінну U_n мож-

¿=1

nX - nu X - Ці-

на записати як U_n =-т=- =-Vn (3.52)

cw n er

і границя (3.48) приймає більш знайому форма запису

( X -и Л

limР -^л/П < x= N(0,1), (3.53)

V ^и )

де N(0,1) - нормальний розподіл з нульовим математичним сподіванням і стандартним відхиленням, рівним одиниці.

У деяких задачах не завжди виконується умова існування однаково розподілених доданків. Сутність цих умов полягає в тому, що жодний з доданків не повинний бути домінуючим, внесок кожного доданка в середнє арифметичне має бути дуже малим у порівнянні з усією сумою.

2. Центральна гранична теорема для неоднаково розподілених доданків - теорема Ляпунова.

Для незалежних неоднаково розподілених випадкових величин Х₁, Х₂, Х_п з математичними сподіваннями ЩХЦ = /г,- і дисперсіями £>[Хі] = а,² Ф0 (і = 1, 2, п) випадкова величини и_п матиме вигляд

пунова переходить у теорему Ліндеберга-Леві (3.49).

Сенс центральної граничної теореми такий: якщо обсяг вибірки п є "достатньо великим", то незалежно від форми розподілу параметра /г генеральної сукупності вибіркове середнє X має розподіл, близький до нормального. Отже, оцінку генерального середнього /г за його вибірковим значенням X можна виконувати на основі нормального розподілу. Схема дослідження може бути такою:

o вибираємо випадковим методом п об'єктів х₁, х₂, х_п з генеральної сукупності (для практичних цілей п повинно бути не менше 30, тобто п>30);

- 1 п

o розраховуємо вибіркове середнє X = -^X_і;

п ,=1 '

o виконуємо статистичне оцінювання і формулюємо висновки на основі нормального розподілу (див., наприклад, розділ 5.4).

Центральна гранична теорема - це клас теорем теорії ймовірностей, що затверджують, що сума великої кількості незалежних (або слабко залежних) випадкових величин має розподіл, близький до нормального.

Дуже важливо те, як діють ті причини, з яких складається сукупний результат вимірювань або спостережень: якщо діють аддитивно (тобто шляхом додавання), то величина x має приблизно нормальний розподіл; якщо муль-типлікативно (тобто дії окремих причин перемножуються), то розподіл x є близьким не до нормального, а до так званого логарифмічно нормального, тобто не x, а має приблизно нормальний розподіл. Якщо ж немає підстав стверджувати, що діє один із цих двох механізмів формування підсумкового результату, то про розподіл випадкової величини x нічого певного сказати не можна.

Запитання. Завдання.

1. Які Ви знаєте прямі експериментальні підтвердження того, що частота здійснення деяких подій близька до ймовірності.

2. В чому є прояв дії так званого закону великих чисел?

3. Прокоментуйте результати дослідів Кетле.

4. Сформулюйте і поясніть теорему Бернуллі.

5. Сформулюйте і поясніть теорему Чебишева. Чим вона відрізняється від теореми Бернуллі?

6. Сформулюйте і поясніть центральну граничну теорему для однаково розподілених доданків (теорему Ліндеберга-Леві).

7. Сформулюйте і поясніть теорему Ляпунова.

8. Повторіть математичні процедури завдань за прикладами 3.16 - 3.18.