Математична статистика - Руденко В.М. - Відмінності у значеннях дисперсій (t-критерій Стьюдента для двох зв'язаних вибірок)

Для перевірки гіпотези щодо дисперсій двох сукупностей, які представлені залежними вибірками використовується критерій Стьюдента і, статистика якого має вигляд:

де s₁ і 8₂ - дисперсії вибірок; п - кількість пар спостережень; г ₁₂ - квадрат коефіцієнта парної кореляції.

Методика перевірки гіпотези аналогічна попередньому прикладу.

Приклад 5.15. Виконати перевірку статистичних гіпотез щодо дисперсій п пар спостережень (емпіричні дані у таблиці рис 5.37).

Послідовність рішення:

o Формулювання гіпотез. Умовам перевірки однаковості дисперсії п пар спостережень відповідає варіант неспрямованих гіпотез:

Н₀: а²₁ = а²₂ (а²₁ не відрізняється від а²₂); Н₁: а²₁ Ф а²₂ (а²₁ відрізняється від а²₂).

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; вибірки зв'язані; виміри проведено за шкалою відношень.

o Вибір статистичного критерію. Згідно з припущеннями цій ситуації відповідає модель двобічного і-критерію Стьюдента:

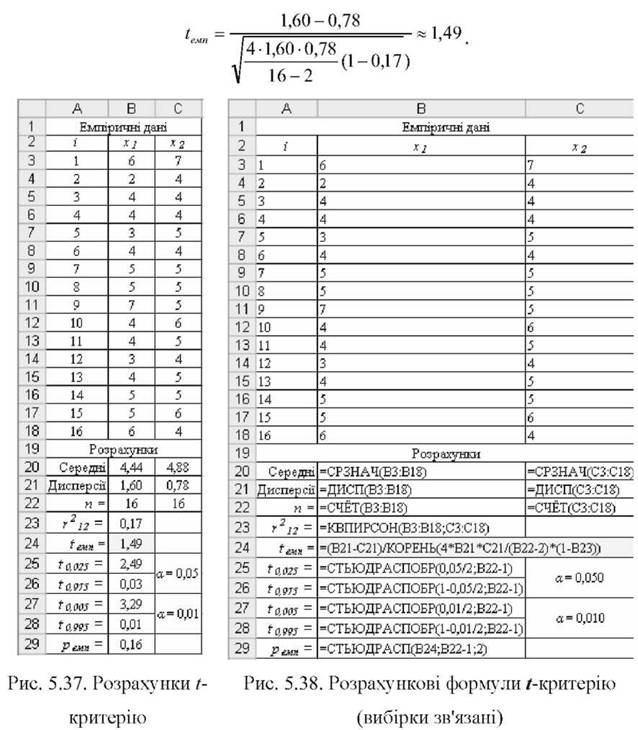
o Розрахунки емпіричного критерію і відповідні формули показано на рис. 5.37 і 5.38. Дисперсії вибірок s₁² ~ 1,60 і s₂² ~ 0,78, а також значення квадрату коефіцієнта кореляції Пірсона r²₁₂ ~ 0,17 розраховано за допомогою функцій MS Excel =ДИСП() і =КВПИРСОН(). Емпіричний критерій приймає таке значення:

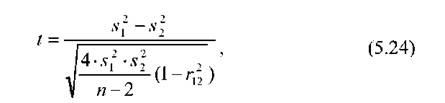
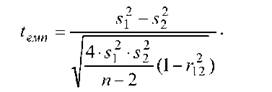
o Визначення критичного значення критерію. Для двобічної моделі встановлюються два критичні значення ґ_кр для точок (а/2) і (1-а/2) і-розподілу з числом ступенів вільності а/=п-2= 16-2=14, тобто: і _а/2 і і _1-а/2. За допомогою функції =СТЬЮДРАСПОБР() для а = 0,05 отримаємо і ₀₀₂₅ ~ 2,49 і і ^₉₇₅ ~ 0,03; для а = 0,01 і 0,005 ~ 3,29 і і 0,995 ~ 0,01 відповідно (рис. 5.37).

o Прийняття рішення. Оскільки значення і _емп~ 1,49 не знаходиться у жодній критичній зоні (0,03 < 1,49 < 2,49), приймається нульова гіпотеза Н₀.

o Формулювання висновків. Навіть на рівні значущості 0,05 немає підстав стверджувати, що показники дисперсій відрізняються одне від одного.

Відмінності у значеннях дисперсій 3-х і більш сукупностей (критерій Кохрана q для вибірок однакових обсягів)

Для перевірки гіпотез про рівність дисперсій 3-х і більш сукупностей використовується критерій Кохрана q.

Приклад 5.16. Виконати перевірку статистичних гіпотез істотності різниць дисперсій трьох незв'язаних вибірок за емпіричними даними рис. 5.39.

Послідовність рішення:

o Формулювання гіпотез:

H₀: а²₁ = а²₂ = а²₃ (дисперсії між собою не відрізняються); H₁: а²₁ Ф а²₂ Ф а²} (дисперсії між собою відрізняються).

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; кількість вибірок більша двох; вибірки незв'язані однакових обсягів; виміри проведено за шкалою інтервалів.

o Вибір критерію. Ситуації відповідає статистика критерію Кохрана q:

_s ²

max __.

^{q =} 2 ? , (5.25)

де s²₁, s²₂, s²_m - дисперсії вибірок; s²_max - максимальна дисперсія; m -кількість вибірок.

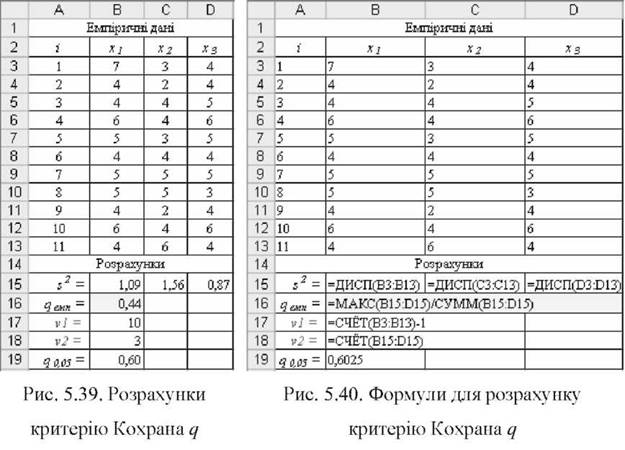
o Результати оцінки емпіричного критерію q_eMn і додаткових параметрів показано на рис. 5.39. Значення дисперсій вибірок s² розраховано за допомогою функції =ДИСП(), для отримання емпіричного критерію q_eM" у комірку В16 введено вираз =MAKC(B15:D15)/CyMM(B15:D15), що відповідає елементарним розрахункам цього критерію:

1,56

_q =---яв 0 44

1,09 +1,56 + 0,87 ' '

o Критичне значення q-критерію Кохрана можна отримати за допомогою табл. 5 Додатків. На рівні значущості а = 0,05 для кількості ступенів вільності у1 = п-1 = 11-1=10 і у2 = т = 3 критичне значення д_{0 05} ~ 0,60.

o Прийняття рішення. Оскільки д_ем"< д_0і05 (0,44 < 0,60) приймається нульова гіпотеза Н₀.

o Формулювання висновків. На рівні значущості 0,05 немає підстав стверджувати про те, що показники дисперсій відрізняються одне від одного.

Одна з переваг методу перевірки статистичних гіпотез за критерієм Кох-рана д є простота обчислень. Недоліком вважається те, що критерій виявляє ознаки відхилення тільки у бік зростання.