Математична статистика - Руденко В.М. - Критерій Фрідмана X2 r

Критерій Фрідмана Хг застосовується для зіставлення показників, виміряних у трьох або більше умовах на одній і тій же вибірці і будується на рангових послідовностях. Критерій х²_г дозволяє встановити факт того, що значення показників від умови до умови змінюються, проте не указує на напрям цих змін.

Гіпотези:

Н₀: між показниками, виміряними в різних умовах, існують лише випадкові розходження;

Н₁: між показниками, виміряними в різних умовах, існують невипадкові розходження.

Обмеження критерію: мінімальна кількість випробовуваних осіб п>2, кожна особа має пройти більше трьох випробувань с>3.

Приклад 5.19. На рис. 5.44 наведено результати самооцінки емпатичних здібностей студентів інституту (за методикою О.П.Єлісєєва). Чи достовірні розходження у значеннях самооцінки студентів у різні роки навчання?

Послідовність рішення:

o Формулювання гіпотез:

Н₀: між показниками самооцінки емпатичних здібностей, виміряними в різні роки, існують лише випадкові розходження;

Н₁: між показниками самооцінки емпатичних здібностей, виміряними в різні роки, існують невипадкові розходження.

o Перевірка обмежень: виміри зроблено за шкалою інтервалів; кількість умов с = 4 (с>3); кількість випробовуваних п =10 (п>2); вибірки зв'язані.

o Розрахунки емпіричного критерію ФрідманаX²_Г (рис. 5.44):

- визначити середнє самооцінки за кожною умовою (для кожного курсу навчання), для чого у комірку В13 внести вираз =СРЗНАЧ(Б3:Б12). Аналогічні вирази внести у комірки С13:Е13;

- проранжувати індивідуальні значення самооцінки для кожного студента (ранжирування за рядками), нараховуючи меншому значенню менший ранг. Для цього у комірку В16 внести вираз

=(СЧЕТ($Б3:$Е3) + 1 - РАНГ(Б3;$Б3:$Е3; 1) -- РАНГ(Б3;$Б3:$Е3; 0))І2+РАНГ(Б3;$Б3:$Е3;1);

- аналогічні вирази внести у комірки всього діапазону В16Е25;

- у комірках В26Е26 підрахувати суми рангів Т за кожною умовою;

- у комірках Р16:Р26 перевірити збіг отриманих сум за рядками і за стовпчиками (суми рангів індивідуальних значень дорівнюватиме 10);

- у комірки В27:В28 внести значення параметрів п і с за допомогою функцій =СЧЕТ(Л3:Л12) і =СЧЕТ(В3:Е3);

- у комірці В29 підрахувати суму квадратів рангів за допомогою виразу =СУММКВ(В26:Е26);

- у комірку В30 внести вираз =12/В27/В28/(В28+1)*В29-3*В27*(В28+1), який дозволить підрахувати значення критерію Хг за формулою:

ХІ = -o£ (Т²) - 3 o п o (с +1), (5.28)

п ■ с ■ (с +1) 7=1

де с - кількість умов; п - кількість випробовуваних осіб.

Як бачимо, значення емпіричного критерію Фрідмана у²_г ~ 15,39.

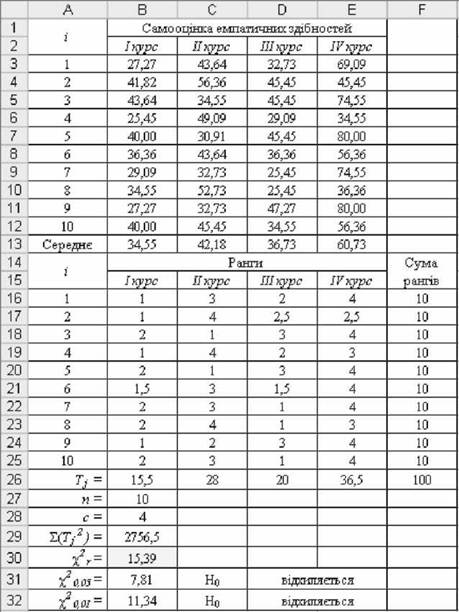
Рис. 5.44. Результати розрахунку критерію Фрідмана Хг

o Визначити критичні значення /²_г-критерію Для а=0,05 і 0,01 можна трьома способами, залежно від параметрів с і n:

- для с = 3 і n < 9 - з табл. 7 Додатків;

- для с = 4 і n < 4 - з табл. 8 Додатків;

- для с>4 або n>9 - за критичними значеннями /^-критерію.

Для а=0,05 і 0,01 і ступенів вільності v = c-l = 4-1= 3 критичні значення Х²о,05 ~ 7,81 і х²о,оі ~ 11,34 отримаємо за допомогою функції Excel =ХИ20БР(), яку необхідно внести у комірки В31 і В32 з відповідними аргументами: =ХИ20БР(0,05;3) і =ХИ20БР(0,01;3).

Прийняття рішення. Оскільки Хг > Хот (15,39>11,34), нульова гіпотеза Н₀ відхиляється на рівні значущості 0,05 і 0,01 (див. рис. 5.44).

o Формулювання висновків. Між показниками самооцінки емпатичних здібностей, виміряними в різні роки навчання студентів, існують невипадкові розходження на рівні значущості 0,01. Проте визначити тенденцію розходжень на підставі критерію Фрідмана неможливо, це дозволяє зробити критерій тенденцій Пейджа L.