Теорія статистики - Мармоза А.Т. - 4.2. Види середніх величин і способи їх обчислення

Залежно від характеру усереднюваної ознаки і наявної вихідної інформації в статистиці застосовуються різні види середніх величин, серед яких найбільше використовуються такі: середня арифметична, середня гармонічна, середня геометрична і середня квадратична.

Поряд з переліченими видами середніх величин в статистичній практиці знаходять застосування також середня хронологічна, середня ковзна, середня прогресивна, середня багатовимірна і так звані структурні середні: мода, медіана та ін.

Кожну середню можна визначити як просту, коли значення варіант спостерігаються тільки один раз або однакову кількість разів, і як зважену, коли значення варіант повторюється різну кількість разів. Уведемо такі позначення і поняття середніх: х - середнє значення досліджуваної ознаки; х - окремі значення усереднюваної ознаки (варіанти);

п - число одиниць досліджуваної сукупності; / - частота повторень (вага) варіант; Щ = х/- обсяг явищ. Ознаку, за якою знаходять середню, називають усередненою ознакою. Величину ознаки кожної одиниці сукупності називають варіантою або значенням досліджуваної ознаки. Частоту повторень варіантів у сукупності називають статистичною вагою.

Середні величини, що застосовуються в статистиці, належать до загального типу степеневих середніх. Відрізняються вони тільки показником степені. Математична статистика виводить різні середні з формули степеневої середньої, яка являє собою корінь к-ої степені з частки від ділення суми індивідуальних значень ознаки к-ої степені на число індивідуальних значень:

де к - показник степені, який визначає тип середньої. Підставляючи у наведену формулу замість к відповідні значення показника степені, одержимо такі середні:

Вибір того чи іншого виду середньої визначається цілями і завданнями дослідження і наявною інформацією.

Загальною умовою правильного обчислення усіх видів середніх є збереження незмінним загального обсягу варіюючої ознаки при заміні індивідуальних значень ознак їхньою середньою. Так, середня арифметична застосовується тоді, коли обсяг варіюючої ознаки утворюється як сума окремих варіант; середня гармонічна - коли обсяг варіюючої ознаки утворюється як сума обернених значень окремих варіант; середня геометрична - коли обсяг варіюючої ознаки утворюється як добуток окремих варіант; середня квадратична - коли обсяг варіюючої ознаки утворюється як сума квадратів окремих варіант.

Розглянемо перелічені вище види середніх більш докладно.

Середня арифметична

Середня арифметична - найпоширеніший вид середньої. Середня арифметична проста являє собою частку від ділення суми індивідуальних значень ознаки на їх загальне число. її обчислюють за формулою:

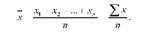
Середня арифметична проста застосовується в тих випадках, коли відомі дані про окремі значення ознаки та їх число в сукупності, тобто розраховується у разі, коли є незгруповані індивідуальні значення ознаки. В статистичній практиці вона застосовується, як правило, для розрахунку середніх рівнів ознак, представлених у вигляді абсолютних показників. Наприклад, якщо є дані про посівну площу овочів у трьох бригадах господарства (га): 47, 65 і 38 і необхідно визначити середній розмір посівної площі, то розрахунок середньої величини необхідно здійснювати за формулою середньої арифметичної простої оскільки значення усереднюваної ознаки зустрічаються однакове число раз (по одному разу):

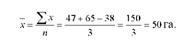
Отже, середній розмір посівної площі з розрахунку на одну бригаду становить 50 га.

Середня арифметична зважена обчислюється із значень варіюючої ознаки з урахуванням ваг. її застосовують у тих випадках, коли значення ознаки представлені у вигляді варіаційного ряду розподілу, в якому чисельність одиниць по варіантах не однакова, а також при розрахунку середньої із середніх при різному обсязі сукупності. Зважування в даному випадку здійснюється за частотами, які показують скільки разів повторюється та або інша варіанта. Формула середньої арифметичної зваженої має вигляд:

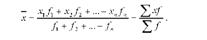
Отже, при обчисленні середньої арифметичної зваженої необхідно всі значення варіант помножити на їхню частоту, одержані добутки підсумувати і цю суму розділити на суму частот, тобто загальний обсяг сукупності.

За аналогічною формулою визначається загальна середня (х"г) з групових середніх (хгр), якщо чисельність одиниць по групах (/Ір) неоднакова:

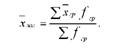
Розглядаючи формулу середньої арифметичної зваженої, можна помітити, що вона не має принципової відміни від простої середньої арифметичної. Тут підсумування / раз одного і того самого варіанта (х) замінюють множенням його на число повторень (частоту -/).

Порядок розрахунку середньої арифметичної у варіаційному ряду розподілу покажемо на прикладі середнього настригу вовни по групі господарств (табл. 4.1).

Таблиця 4.1. Дані для розрахунку середньої арифметичної зваженої

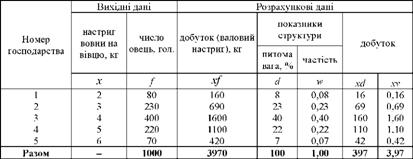
Оскільки значення усереднюваної ознаки (настриг вовни) повторюється неоднакове число раз, то середній настриг вовни визначимо за формулою середньої арифметичної зваженої:

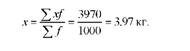
При розрахунку середньої арифметичної зваженої частотами (вагами) можуть бути використані відносні показники структури, виражені в процентах або коефіцієнтах (частках). Методика розрахунку середньої і кінцевий результат при цьому не зміняться.

Якщо частоти виражені в процентах, то формула середньої арифметичної зваженої може бути записана в такому виді:

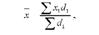
де і, = -100 - питома вага кожної частини в загальному обсязі всіх частот (в процентах).

Оскільки для всієї сукупності £ сі' = 100%, то формулу можна записати так:

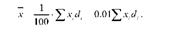
Якщо частоти виражені в коефіцієнтах (частках), £ 1, тоді формула середньої спрощується:

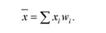
Порядок і послідовність розрахунку середньої арифметичної для випадків, коли вагами використовуються відносні показники структури, розглянемо на даних того самого прикладу (табл. 4.1).

Якщо вагами взяті частоти, виражені в процентах, то середній настриг вовни на вівцю становитиме:

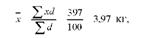
а якщо частості: х = £, = 0,16 + 0,69 +1,60 +1,10 + 0,42 = 3,97 кг.

Отже, одержані ті самі результати як і при розрахунку середньої арифметичної зваженої звичайним способом.

Для інтервальних варіаційних рядів розподілу, в яких значення ознаки дано в межах "від - до", середню арифметичну зважену знаходять в такій послідовності. Спочатку необхідно інтервальний ряд розподілу перетворити в дискретний. Для цього по кожному інтервалу знаходять його середину (центр). Серединне значення інтервалу звичайно визначають як півсуму його нижньої і верхньої меж. Наприклад, для інтервального ряду розподілу господарств за надоєм молока на корову (ц): 26 - 28, 28 - 30, 30 - 32 і т.д. серединами інтервалів будуть (ц): 27 = (26+28):2; 29 = (28+30):2; 31 = (30+32):2 і т.д.

Якщо є інтервали з нечітко вираженими межами, з так званими "відкритими межами" (перший інтервал "до" і останній - "понад"), то для визначення серединного значення потрібно встановити умовні межі цих інтервалів. Звичайно в цих випадках вирішують так: для першого інтервалу беруть величину другого інтервалу, а для останнього - величину передостаннього інтервалу.

Покажемо перехід від інтервалів з відкритими межами до інтервалів із закритими межами на такому прикладі розподілу господарств за середньодобовим прирістом відгодівельного поголів'я свиней (г):

відкриті інтервали до 350 350 - 400 400 - 450

450 - 500

понад 500

закриті інтервали

300 - 350 350 - 400 400 - 450 450 - 500 500 - 550.

Після того як знайдені середини інтервалів, середню арифметичну зважену обчислюють так, як і в дискретному ряду розподілу: значення варіант множать на частоти і одержану суму добутків ділять на суму частот.

Порядок розрахунку середньої арифметичної в інтервальному ряду розподілу розглянемо на прикладі розподілу 100 господарств за надоєм молока на корову (табл. 3.10). Всі розрахунки зведемо в табл. 4.2.

Таблиця 4.2. Дані для розрахунку середньої арифметичної в інтервальному ряду розподілу

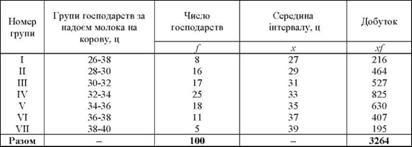
Середній надій на корову знайдемо за середньою арифметичною зваженою:

Обчислення середньої з інтервального ряду розподілу має деякі особливості, пов'язані з визначенням середини інтервалу. Визначення варіанти як півсуми верхньої і нижньої меж виходить з припущення, що індивідуальні значення ознаки всередині інтервалу розподіляються рівномірно і, отже, середні значення інтервалів досить близько примикають до середньої арифметичної в кожній групі. В дійсності це не завжди так, тому середні, обчислені з інтервальних рядів, є приблизними.