Теорія статистики - Мармоза А.Т. - 6.5. Поняття статистичної оцінки. Точкова і інтервальна оцінка параметрів генеральної сукупності

Оскільки всі елементи генеральної сукупності для обчислення шуканого параметра, як правило, використати неможливо, то про цей параметр намагаються судити за даними однієї або кількох вибірок із генеральної сукупності.

Наближене значення шуканого параметра генеральної сукупності, встановлене за даними вибіркової сукупності, називають вибірковою оцінкою параметра.

Якщо шуканий параметр генеральної сукупності позначити через 0 , а

значення вибіркової характеристики - через 0 , то характеристика 0 в даному випадку виступає як оцінка параметра генеральної сукупності 0 .

В зв'язку з тим, що значення вибіркових характеристик встановлюються за даними випадкових вибірок, то і самі оцінки є випадковими величинами.

Оцінка параметрів є одним із центральних завдань математичної статистики і являє собою сукупність методів, які дозволяють робити науково обґрунтовані висновки щодо параметрів генеральної сукупності за даними випадкової вибірки з неї.

Оцінкою генеральної середньої (математичного сподівання) може виступати вибіркова середня, генеральної частки - вибіркова частка, генеральної дисперсії - вибіркова дисперсія тощо.

Для того щоб статистичні оцінки давали найкращі та добрі наближення оцінюваних параметрів, вони повинні володіти певними властивостями і задовольняти певним вимогам. Основними властивостями оцінок є властивості незміщеності, спроможності, ефективності і достатності.

Незміщеною називають статистичну оцінку 9 , математичне сподівання якої дорівнює оцінюваному параметру 9 при будь-якому обсязі вибірки, тобто якщо вона задовольняє рівності

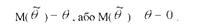
Оцінка називається зміщеною, якщо її математичне сподівання не дорівнює оцінюваному параметру, тобто М( 9 ) ф 9 .

Оцінка 9 параметра 9 називається спроможною, якщо вона підпорядковується закону великих чисел, тобто при п -"со наближається за імовірністю до шуканого параметра:

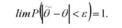
Спроможність оцінки означає, що чим більше обсяг вибірки, тим більша імовірність того, що помилка оцінки не перевищить скільки завгодно малого додатного числа є.

Ефективною називають таку незміщену оцінку 9 , яка має найменшу дисперсію серед усіх можливих незміщених оцінок параметра 9 , обчисленого за вибірками одного і того самого обсягу.

Оцінка 9 називається достатньою (вичерпною), якщо вона включає всю інформацію, яка міститься у вибірці відносно шуканого параметра 9 .

Основними методами отримання оцінок параметрів генеральної сукупності за даними вибірки є методи моментів, аналогії, найменших квадратів, максимальної правдоподібності та ін.

З усіх перерахованих методів найбільш широко застосовується метод максимальної (найбільшої) правдоподібності. Суть цього методу, розробленого видатним англійським математиком-статистиком Р.Й.Фішером, полягає в тому, що із можливих оцінок параметра в вибирається та, якій відповідає найбільша імовірність, тобто те значення, яке обертає функцію в максимум. Вибіркова оцінка 0 , яка обертає в максимум функцію правдоподібності, називається оцінкою максимуму правдоподібності.

Метод максимуму правдоподібності дозволяє одержати спроможні, ефективні, достатні та незначно зміщені оцінки.

Використовуючи метод максимуму правдоподібності можна довести, що вибіркова середня арифметична є незміщеною, спроможною. ефективною і достатньою оцінкою генеральної середньої, а вибіркова дисперсія є найкращою оцінкою генеральної дисперсії. Цим значною мірою і пояснюється перевага, яка надається даним характеристикам порівняно з усіма іншими вибірковими характеристиками.

В теоретичному курсі математичної статистики доводиться, що математичне сподівання вибіркової дисперсії не дорівнює дисперсії генеральної сукупності. Тому вибіркова дисперсія є зміщеною оцінкою генеральної дисперсії.

Для отримання незміщеної оцінки дисперсії генеральної сукупності необхідно вибіркову дисперсію (О" ) помножити на так звану поправку Бесселя

П-1. Тоді виправлена або скоригована дисперсія (8 ) може бути визначена за формулою

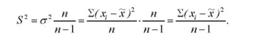
Математичне сподівання такої виправленої вибіркової дисперсії при будь-якому обсязі вибірки дорівнює генеральній дисперсії. При достатньо великій чисельності вибірки поправка Бесселя п-1", яка корегує зміщення вибіркової дисперсії, практично дорівнює одиниці і тому нею можна знехтувати. При п > 30 (великі вибірки) практично немає різниці між оцінками ст і 5 . При малих же значеннях (п < 30; малі вибірки) поправочний коефіцієнт значно відрізняється від одиниці. Тому при малому обсязі вибірки завжди потрібно користуватися незміщеною оцінкою дисперсії 52. Можна довести, що оцінки ст і 5 - є спроможними оцінками генеральної дисперсії &0 .

Оцінка невідомого параметра генеральної сукупності може бути проведена двояко: або одним числом (точкою) - точкова оцінка, або із зазначенням інтервалу, в якому із заданою імовірністю може знаходитись шуканий параметр, - інтервальна оцінка.

Суть точкової оцінки полягає в тому, що за найкращу оцінку шуканого параметра генеральної сукупності в приймається знайдене за вибіркою його конкретне числове значення в , тобто приймається припущення, що 0=0.

Оскільки сама вибіркова оцінка є випадковою величиною, а статистичні висновки в зв'язку з цим мають імовірнісний характер, то конкретна числова характеристика (точка) обов'язково повинна бути доповнена величиною середньої помилки (и). Розміри помилки оцінки безпосередньо пов'язані з величиною її дисперсії (розсіювання): чим менше дисперсія, тим менше помилка оцінки, тим надійніше статистичні висновки. Тому дисперсію на практиці ототожнюють з помилкою оцінки, а середньоквадратичне відхилення вибіркової оцінки називають середньою помилкою.

Середню помилку оцінки в загальному вигляді визначають за формулою:

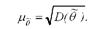
Квадрат середньої помилки (дисперсія вибіркових середніх) прямо пропорційний дисперсії ° і обернено пропорційний чисельності вибірки п:

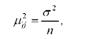
звідки формула для визначення середньої помилки оцінки прийме вигляд:

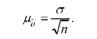
Отже, визначивши за вибіркою середнє квадратичне відхилення, можна встановити значення середньої помилки оцінки, величина якої, як випливає із формули, тим більша, чим більша варіація випадкової величини і тим менша, чим більша чисельність вибірки.

Результати точкової оцінки шуканого параметра генеральної сукупності можна записати таким чином: за статистичну оцінку параметра генеральної

сукупності приймається його вибіркове значення (0 = 0 ) з середньою помилкою ±Мц .

При невеликому обсязі вибірки точкова оцінка значною мірою випадкова і малоефективна і тому може істотно відрізнятися від параметра генеральної

сукупності, тобто призводити до великих відхилень 0-0 . З цієї причини при невеликому обсязі вибірки доцільно користуватися інтервального оцінкою.

Інтервального називають оцінку, яка визначається двома числами - кінцями інтервалу, в якому із заданою імовірністю знаходиться шуканий параметр. Центром такого інтервалу, як правило, беруть знайдену вибіркову оцінку точки, а визначення самих кінців інтервалу пов'язується з середньою помилкою оцінки і довірчою імовірністю. Отже, інтервальна оцінка є подальшим доповненням і розширенням точкової оцінки параметра 0.

Встановивши довірчу імовірність, можна побудувати довірчий інтервал. Довірчим інтервалом для параметра 0 називається такий інтервал, відносно якого можна із заздалегідь встановленою довірчою імовірністю Р = 1 - а, близькою до одиниці, стверджувати, що він містить невідоме значення параметра 0. Іншими словами, це інтервал, який покриває невідомий параметр 0 із заданою імовірністю Р.

Для побудови довірчого інтервалу необхідно вказати таке граничне значення помилки єр = (в-в), щоб імовірність її перевищення була не більше а, тобто

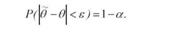
Отже, інтервальна оцінка параметра в-в±єр, а довірчий інтервал (Ір) має вигляд

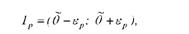
де в ер - початок інтервалу; @ +єр - кінець інтервалу.

Наприклад, шуканий довірчий інтервал для оцінки генеральної середньої матиме вигляд:

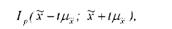
де іц-Ер - гранична помилка оцінки.

Для побудови надійного інтервалу спочатку необхідно визначити помилку вибірки, а потім за таблицями значень функції Лапласа (дод. 2) при заданому рівні імовірності знайти значення і.

Визначивши значення вибіркової оцінки і середньої помилки вибірки, можна при заданому рівні імовірності або відомому нормованому відхиленні (аналогічно побудові надійного інтервалу для оцінки генеральної середньої) побудувати довірчий інтервал і для оцінок інших вибіркових характеристик розподілів (наприклад, моди, медіани, дисперсії, частки та ін.).

Загальний вид довірчого інтервалу такий

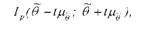
де Цд - середня помилка оцінки, що використовується, і визначається як ^Щв ) .

Ширина довірчого інтервалу безпосередньо залежить від величини граничної помилки, яка в свою чергу залежить від величини дисперсії (розсіювання) оцінки. Отже, чим менше дисперсія вибіркової оцінки, тим вужче довірчий інтервал, тим точніше і надійніше статистичні висновки.

В зв'язку з цим основна організаційна робота вибіркового спостереження полягає в тому, щоб прийняти міри, спрямовані на зменшення дисперсії. Дисперсія оцінки суттєво залежить від способів формування і відбору одиниць у вибіркову сукупність.

Проведемо точкову і інтервальну оцінку генеральної середньої за даними великої вибірки на такому прикладі. Є дані щодо стажу роботи 30 трактористів: 2; 5; 15; 7; 18; 20; 9; 6; 18; 15; 4; 16; 25; 8; 30; 1; 26; 20; 21; 6; 35; 30; 18; 26; 31; 3; 24; 32; 17; 22. Довірчий рівень імовірності Р = 0,9545, якому відповідає і = 2.

Для визначення середньої помилки вибірки визначимо середню арифметичну і дисперсію.

Середній стаж роботи трактористів

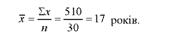
Вибіркова дисперсія

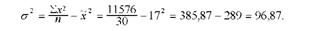
Скоригована дисперсія

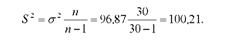
Незміщена оцінка дисперсії може бути визначена і за іншою формулою:

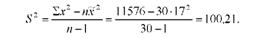
Середня помилка вибіркової середньої

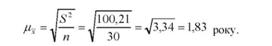
Проведемо точкову оцінку середнього стажу роботи в генеральній сукупності:

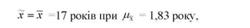
тобто точкова оцінка генеральної середньої може бути записана так:

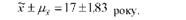
Це означає, що х = 17 років є оцінкою генеральної середньої з помилкою, що дорівнює 1,83 року.

Для проведення інтервальної оцінки і побудови довірчого інтервалу визначимо граничну помилку вибіркової середньої при Р = 0,9545 і і = 2. Гранична помилка вибіркової середньої

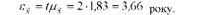
Побудуємо довірчий інтервал, в якому із заданим рівнем імовірності знаходиться середній стаж роботи трактористів в генеральній сукупності:

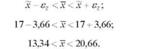
Таким чином, довірчі межі інтервалу

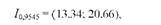
що можна записати так: х = 17 ± 3,66 року.

Отже, з довірчою імовірністю Р = 0,9545 можна стверджувати, що середній стаж роботи трактористів у генеральній сукупності знаходиться в інтервалі 13,34 - 20,66 року.

Точкова і інтервальна оцінка генеральної середньої в малих вибірках (п < 30) проводиться аналогічно оцінці у великих вибірках лише з тією різницею, що при визначенні граничної помилки замість і-критерію нормального розподілу використовується і - критерій Стьюдента (дод. 3).