Теорія статистики - Мармоза А.Т. - Нормальний розподіл

Під законом розподілу слід розуміти такий теоретичний розподіл до якого прямує емпіричний розподіл при п -" со.

В статистиці широко використовуються різні види теоретичних розподілів, серед яких класичними вважаються нормальне, біноміальне і пуассонове. Серед названих законів розподілу, на якому ґрунтується більшість статистичних методів дослідження, є закон нормального розподілу.

Окремі закони пов'язані з характером розподілу окремих випадкових величин і застосовуються для розв'язання конкретних задач. Ці закони носять імена вчених, які їх відкрили. Серед них у статистичній науці і практиці найбільш широке застосування одержали закони розподілу Стьюдента, Пірсона і Фішера-Снедекора.

Кожний із законів розподілу має свою специфіку і область застосування в різних галузях знання.

Закони розподілу в основному використовуються для розв'язування задач, пов'язаних з оцінкою параметрів генеральної сукупності і перевіркою статистичних гіпотез.

Розглянемо закони розподілу, що одержали в статистичному аналізі найбільше застосування.

Нормальний розподіл

Більшість соціально-економічних і природних явищ підпорядковано закону нормального розподілу. Підпорядкованість закону нормального розподілу проявляється тим точніше, чим більше випадкових величин діє разом. Якщо жодна з випадково діючих причин за своєю дією не виявиться переважною над іншими, то закон розподілу дуже близько підходить до нормального.

Така закономірність проявляється, наприклад, в розподілі відхилень у виробничому процесі при нормальному рівні організації і технології, в розподілі населення певного віку за розміром взуття, одягу і в багатьох інших випадках.

Нормальний розподіл є симетричним розподілом, в якому більшість значень випадкової величини концентрується навколо середньої величини, його особливістю є те, що чим більше значення окремих варіант відхиляються від середньої величини, тим рідше вони зустрічаються і тим менше імовірність їх появи. І навпаки, чим ближче варіанти до середнього значення, тим частіше вони зустрічаються і тим більше імовірність їх появи. Однакові за абсолютним значенням, але протилежні за знаком відхилення значень змінної х від середньої рівно імовірні.

Імовірність відхилень вибіркових середніх від генеральної середньої (~ - х) при великому числі спостережень (п -"со) визначається законом нормального розподілу Лапласа-Гаусса.

Нормальним розподілом називають розподіл неперервної випадкової величини, який описується щільністю імовірності

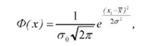
де Ф(х) - щільність імовірності (ордината кривої); ст0 - середнє квадратичне відхилення генеральної середньої, яке у практичних розрахунках замінюється вибірковим ст; к = 3,14 ... (постійна величина, яка характеризує відношення довжини кола до довжини його діаметра); е = 2,718... - основа натуральних логарифмів (число Ейлера).

Як видно, нормальний розподіл визначається двома параметрами: середньою арифметичною і середнім квадратичним відхиленням. Знаючи ці параметри, можна побудувати криву нормального розподілу.

Звичайно в даній формулі замінюється на і, де відхилення представлені в частках середнього квадратичного відхилення, прирівняного до одиниці. Завдяки нормуванню, дисперсія і = 1, а х = 0.

Рівняння нормальної кривої при такій заміні приймає вигляд:

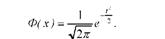
Його називають стандартним рівнянням нормальної кривої, а нормальну криву - нормованою кривою. При її побудові за емпіричними даними застосовують таку формулу

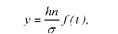
де у - ордината кривої (теоретична частота); Ь - величина інтервалу; п - чисельність сукупності; ег - середнє квадратичне відхилення; /(і) - функція щільності нормального розподілу.

Графік щільності нормального розподілу називається нормальною кривою або кривою Гаусса (рис. 8.1).

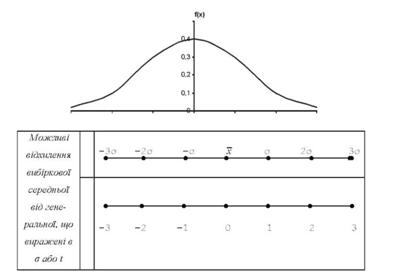
Рис. 8.1. Крива нормального розподілу імовірностей

Ця дзвоноподібна крива симетрична відносно осі ординат і асимптотично наближається до осі абсцис. Крива має точки перегину при і = ±1, тобто при таких відхиленнях значень ознаки від середньої арифметичної, які дорівнюють одному середньому квадратичному відхиленню. Площа, що обмежена кривою і віссю абсцис, дорівнює одиниці. Значення щільності імовірності Ф(х) залежить тільки від величини нормованого відхилення і, так як я і е - постійні величини. Так, при і = 0 співмножник е 2 = 1 і щільність імовірності максимальна Ф(0) = 0,3989. Мірою зростання і щільність імовірності зменшується.

Для знаходження значень інтеграла імовірностей при заданому і складені спеціальні таблиці (дод. 2), за якими можна визначити значення і при заданому рівні імовірності Р і значення Р імовірності при відомому і.

Теоретичні значення і і Р, що обчислені на основі стандартного рівняння нормальної кривої, використовуються в математичній статистиці, зокрема, у вибірковому методі, як нормативи (критерії), за допомогою яких проводиться оцінка вибіркових характеристик. В зв'язку з цим нормоване відхилення кривої нормального розподілу отримало назву і - критерію розподілу нормальної кривої.