Теорія статистики - Мармоза А.Т. - 7.4. Перевірка статистичних гіпотез щодо середніх величин

Серед найважливіших узагальнюючих характеристик, відносно яких найчастіше висуваються гіпотези, є середня величина. З метою перевірки гіпотези про рівність середніх в генеральній сукупності необхідно сформулювати нульову гіпотезу. При цьому, як правило, виходять з того, що обидві вибірки узяті з нормально розподіленої генеральної сукупності з математичним сподіванням, рівним X і з дисперсією, рівною с0 . Якщо це припущення вірне, то х1 - х2 ~ х . Фактично ж вибіркові середні Х1 І Х2 не будуть рівні через випадковості вибірки. Тому потрібно з'ясувати істотність розбіжностей між х1 х2 - чи знаходиться їх різниця в межах можливої випадкової варіації чи ж вона виходить за ці межі. Тоді задача перевірки гіпотези зводиться до перевірки істотності різниці

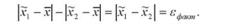
Кожна вибіркова середня має свою помилку /і:

Визначивши дисперсії і середню помилку вибіркових середніх, можна обчислити фактичне значення І-критерію і порівняти його з критичним (табличним) значенням при відповідному рівні значущості і числі ступенів свободи варіації (для вибірок з чисельністю п > 30 використовується і-критерій нормального розподілу, а для вибірок з чисельністю п < 30 - і-критерій Стьюдента).

Фактичне значення і-критерію визначається за формулою

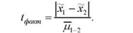
Якщо вибіркове значення критерію потрапляє в критичну область (їфакі> О, нульова гіпотеза про рівність середніх відхиляється; якщо ж вибіркове значення критерію потрапляє в область припустимих значень (Іфакг< їа), нульова гіпотеза приймається.

Нульова гіпотеза про рівність середніх у двох генеральних сукупностях може бути також перевірена шляхом порівняння фактичної середньої різниці [єФа,.т = ~~2) з граничною випадковою помилкою при заданому рівні значущості (єа). Якщо фактична різниця між вибірковими середніми знаходиться в межах випадкової помилки (єфакт < єа), нульова гіпотеза приймається. Якщо ж фактична різниця між середніми виходить за межі випадкової помилки (еф^т > єа), нульова гіпотеза відхиляється.

При розв'язуванні конкретних задач по перевірці статистичних гіпотез відносно середніх необхідно враховувати такі моменти: 1) схему формування вибірок (вибірки незалежні і залежні); 2) рівність або нерівність обсягів вибірок; 3) рівність або нерівність дисперсій в генеральних сукупностях.

Алгоритм перевірки гіпотези відносно двох середніх дещо змінюється, якщо дисперсії по вибірках (512 і 522) суттєво відрізняються. В цьому випадку при визначенні числа ступенів свободи вводиться поправка:

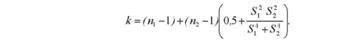
Коли ж при нерівних дисперсіях по вибірках, нерівними є і їх чисельності (п1 і п2), табличне значення г-критерію Стьюдента слід розрахувати за формулою

де і1 і і2 - табличні значення Г-критерію Стьюдента, які беруться відповідно з п1 - 1 і п2 - 1 ступенями свободи.

Розглянемо приклад перевірки статистичної гіпотези про рівність двох середніх незалежних вибірок рівної чисельності (п1=п2) і рівними дисперсіями (СГ;2 = ).

Нехай, є дані щодо живої маси телят при народжені по двох групах корів чорно-рябої породи (корови одного віку). Перша група корів мала нормальну тривалість лактації (305 днів), а друга група доїлася протягом 320 днів. У кожну групу відібрано по 5 корів. Дані спостереження наведено в табл. 7.2.

Таблиця 7.2. Жива маса телят при народжені по групах корів з різною тривалістю лактації

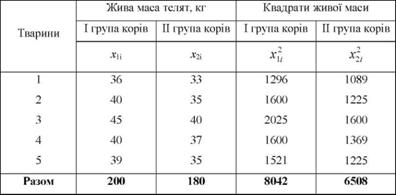
Співставлення живих мас телят по двох групах корів показує, що більш висока жива маса телят спостерігається у корів І групи, які мали нормальну тривалість лактації. Однак, в зв'язку з тим, що чисельність вибірок невелика (п = 5), не виключена можливість, що розбіжності між живими масами отримані в результаті дії випадкових причин.

Потрібно статистично оцінити різницю між середніми по двох групах корів.

За результатами перевірки гіпотези зробити висновок про те, що різниця між середніми лежить в межах випадкових коливань, або ж ця різниця настільки значна, що не узгоджується з нульовою гіпотезою про випадковий характер відмінностей між середніми.

Якщо буде доведено друге положення і відхилене перше, можна стверджувати, що тривалість лактації впливає на живу масу телят.

Умова задачі передбачає, що обидві вибірки взяті із нормально розподіленої генеральної сукупності. Формування груп випадкове (незалежне), тому оцінюватись повинна різниця між середніми.

Визначимо середню живу масу телят по двох групах корів:

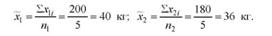
Фактична різниця між середніми становить:

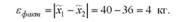
Істотність цієї різниці повинна бути оцінена. Для цього необхідно перевірити гіпотезу про рівність двох середніх.

Розглянемо докладно всі етапи схеми перевірки гіпотези. 1. Сформулюємо нульову Но і альтернативну На гіпотези:

2. Приймемо рівень значущості а = 0,05, гарантуючи прийняття гіпотези або відмови від неї з імовірністю помилки тільки в 5 випадках із 100.

3. Найпотужнішим критерієм для перевірки такого роду гіпотези Н0 є і-критерій Стьюдента.

4. Сформулюємо правило прийняття рішення за результатами

перевірки Н0. Оскільки за альтернативною гіпотезою х1 може бути або менше або більше х2 , то критична область повинна бути встановлена з двох

сторін: і - ~іа і і - іа , або коротше: іа .

Така форма завдання критерію називається двосторонньою критичною областю. Критична область при а = 0,05 буде міститись в межах - всі значення вище, ніж верхня 2,5% і нижче, ніж 2,5% точки розподілу і-критерію Стьюдента.

З урахування сказаного висновки по перевірці Н0 можна сформулювати так: гіпотеза Н0 відхиляться, якщо фактичне значення Г-критерію виявиться

більшим за табличне значення, тобто якщо іфакт > іа . В протилежному випадку Но повинна бути прийнята.

5. Щоб перевірити Н0 потрібно визначити фактичне значення Г-критерію Стьюдента і порівняти його з табличним значенням.

Для визначення фактичного значення Г-критерію Стьюдента виконаємо такі обчислення.

6. Обчислимо по кожній вибірці скориговані на втрату ступенів свободи варіації дисперсії. Для цього попередньо піднесемо до квадрату значення хц і х2і:

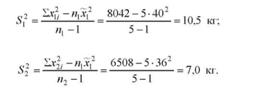
7. Розрахуємо квадрати середніх помилок по кожній вибірці і узагальнену середню помилку різниці середніх:

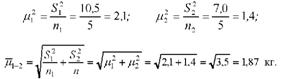
8. Розрахуємо фактичне значення Г-критерію Стьюдента:

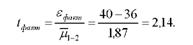
9. Встановимо табличне значення критерію Г-Стьюдента, виходячи із рівня значущості а = 0,05 і загального числа ступенів свободи для двох вибірок:

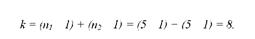
За таблицею "Критичні точки розподілу Стьюдента" (дод. 3) знайдемо і при а = 0,05 і к = 8: і005 = 2,31.

10. Співставимо фактичне і табличне значення і-критерію Стьюдента:

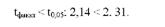
Оскільки іфаккг < і^05 (вибіркове значення критерію знаходиться в області припустимих значень), нульова гіпотеза про рівність середніх в генеральних сукупностях приймається.

Отже, вплив тривалості лактації на живу масу телят при народженні виявляється недоведенним.

Однак слід звернути увагу на такий суттєвий момент: жива маса телят при народженні по всіх спостереженнях досліду вище в першій групі корів, які мають нормальну тривалість лактації. Тому замість альтернативної гіпотези На : х1 ф х2 може бути взята інша. Оскільки немає підстав вважати, що при нормальній тривалості лактації жива маса телят буде нижчою, то очевидно, що більш доцільною формою альтернативної гіпотези є: На : х1 > х2.

Тоді критична область, що становить 0,05 всієї площі під кривою розподілу, буде розташована тільки з одного (правого) боку, так як від'ємні значення живих мас вважаються несумісними з умовами задачі. В зв'язку з цим табличне значення і-критерію слід визначати при подвоєному значенні рівня значущості (тобто при 2а; іа = 2 o 0,05 = 0,10). Критерій перевірки гіпотези формулюється так: нульова гіпотеза відхиляється, якщо > і2а.

Така форма завдання критичної області називається односторонньою. Односторонній критерій більш чутливий до помилок другого роду, але його застосування припустимо лише у випадку, якщо доведена правомірність даної альтернативної гіпотези.

Встановимо за таблицями (дод. 3) табличне значення і-критерію при а = 0,10 і к = 8, і0Д0 = 1,86.

Отже, при використанні одностороннього критерію нульова гіпотеза відхиляється, Тобто критерій виявиться в критичній області (іфакг > і0д0; 2,14 > 1,86). Таким чином, жива маса телят при народженні в групі корів з нормальною тривалістю лактації суттєво вище. Цей висновок точніший, ніж отриманий на основі двостороннього критерію, так як тут використана додаткова інформація для обґрунтування правильності застосування одностороннього критерію.

Такий самий висновок одержимо і шляхом порівняння можливої граничної помилки двох вибірок єа з фактичною різницею середніх.

Обчислимо можливу граничну помилку різниці середніх по двох вибірках: є0до = Г010 o /А_2 = 1,86 o 1,87 = 3,48 кг і порівняємо її з фактичною різницею середніх:

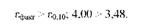
Зіставляючи граничну можливу помилку з фактичною різницею середніх, можна зробити аналогічний висновок про те, що висунута гіпотеза про рівність середніх не узгоджується з одержаними результатами.

Перевірку гіпотези для випадку залежних вибірок з рівними чисельностями і рівними дисперсіями розглянемо на такому прикладі.

Нехай, є дані вибіркового спостереження щодо продуктивності корів-матерів і корів-дочок (табл. 7.3).

Таблиця 7.3. Продуктивність корів-матерів і корів-дочок

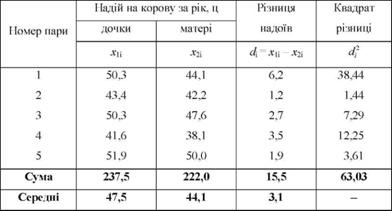
Необхідно перевірити статистичну гіпотезу відносно середньої різниці між парами взаємопов'язаних спостережень в генеральній сукупності.

Оскільки спостереження двох вибірок попарно взаємопов'язані (залежні вибірки), то необхідно порівнювати не різницю між середніми, а середнє значення різниць між парами спостережень (і ). Розглянемо всі етапи процедури перевірки гіпотези. 1. Сформулюємо нульову і альтернативну гіпотези:

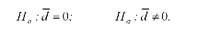
При такій альтернативі необхідно застосувати двосторонній критерій.

2. Рівень значущості приймемо рівним а = 0,05.

3. Найпотужнішим критерієм перевірки Н0 є і-критерій Стьюдента.

4. Обчислимо середню різницю

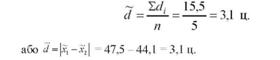
5. Розрахуємо скориговану дисперсію середньої різниці:

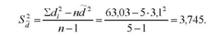
6. Визначимо середню помилку середньої різниці:

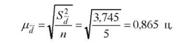
7. Обчислимо фактичне значення і-критерію Стьюдента:

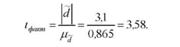
8. Встановимо число ступенів свободи, виходячи із чисельності пар взаємопов'язаних різниць:

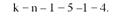
9. Знайдемо табличне значення Г-критерію Стьюдента при к = 4 і а = 0,05; V. = 2,78 (дод. 3).

10. Порівняємо фактичне і табличне значення критерію:

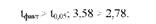
Фактичне значення критерію вище за табличне. Отже, величина середньої різниці між надоями двох вибірок істотна і нульова гіпотеза відхиляється.

Такі самі висновки дістанемо, порівнюючи можливу граничну помилку з фактичною середньою різницею:

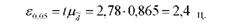
Гранична помилка показує, що в результаті випадкового варіювання середня різниця може досягати 2,4 ц. Фактична середня різниця вище:

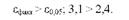
Отже, за результатами досліду можна з високим ступенем імовірності стверджувати, що відмінності в значеннях середніх надоїв корів-матерів і корів-дочок вірогідні.