Теорія статистики - Мармоза А.Т. - 12.3. Види статистичних графіків і способи їх побудови

Статистичні графіки відрізняються великою різноманітністю. Залежно від способу побудови їх можна поділити на дві великі групи: 1) діаграми і 2) статистичні карти.

Діаграми - це умовне зображення числових величин та їх співвідношень за допомогою геометричних знаків. Термін "діаграма" тотожний терміну "статистичний графік". Діаграми є найбільш розповсюдженим видом графіків. Виділяють такі основні види діаграм: лінійні, стовпчикові, стрічкові, квадратні, секторні, радіальні, трикутні, фігурні, знак Варзара та ін.

Залежно від кола розв'язуваних завдань усі діаграми можна поділити на діаграми порівняння, структури та динаміки.

Розглянемо методику і техніку побудови статистичних графіків, що найчастіше застосовуються на практиці.

Найрозповсюдженішим видом показових діаграм є лінійні діаграми, які використовуються здебільшого для характеристики динамічних рядів та рядів розподілу. Поряд з цим лінійні діаграми широко використовуються для вивчення взаємозв'язків між явищами, порівняння кількох показників, ходу виконання планів тощо.

Лінійні діаграми дають можливість зображати явища у вигляді ліній, які з'єднують точки, розташовані у координатному полі. Ламані лінії, що утворюються, показують характер розвитку явища у часі або особливості його розподілу за величиною якої-небудь ознаки, або зв'язку явищ.

За способом побудови - це графіки з рівномірною (арифметичною) шкалою. При їх побудові використовують прямокутну систему координат. Розташування будь-якої точки в цій системі визначається двома параметрами - абсцисою та ординатою. Іноді поле в межах осей координат для зручності нанесення геометричних знаків та читання графіка покривається горизонтальними і вертикальними лініями, проведеними за прийнятим масштабом. Ці лінії утворюють координатну числову сітку.

На горизонтальній осі (вісь абсцис) відкладають однакові за довжиною відрізки, що відображають періоди (роки, місяці, декади, дні і т.д.). На вертикальній осі (вісь ординат) у певному масштабі наносять значення досліджуваної величини. На перетині перпендикулярів відповідних значень досліджуваної ознаки і часових дат до осей координат отримують точки. Ламана лінія, яка з'єднує ці точки, характеризує зміну досліджуваного явища у часі.

Побудову простої лінійної діаграми розглянемо на такому прикладі (табл. 12.1).

Таблиця 12.1. Динаміка виробництва молока в агрофірмі за 2001 - 2010 рр.

В прямокутній системі координат на ось абсцис нанесемо показники часу (роки з 2001 по 2010), беручи масштаб річного періоду таким, що дорівнює 1 см. Тоді довжина горизонтальної шкали буде дорівнювати 10 см (1 см х 10 років). На осі ординат виходячи із оптимального співвідношення осей ординат і абсцис як 1 : 1,5, тобто завдовжки 6,7 см (10 : 1,5), нанесемо в певному масштабі значення валового виробництво молока від 26 до 38 тис. ц. Візьмемо 1 см за 2 тис. ц. При цьому для більшої наочності на осі ординат зробимо розрив, оскільки мінімальне значення виробництва молока значно відрізняється від нуля. На полі графіка точками відкладемо відповідні значення валового виробництва молока по роках. Отримані точки з'єднаємо відрізками прямої лінії (рис. 12. 1).

Побудований графік показує постійне зростання виробництва молока. Ламана крива, яка має невеликі зламування, безперервно прямує вгору.

Лінійні діаграми можуть бути побудовані з метою вивчення взаємозв'язків між двома ознаками: результативним і факторним (наприклад, між урожайністю і якістю ґрунтів). При цьому на осі абсцис відкладають

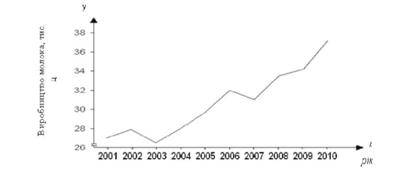
Рис. 12.1. Динаміка валового виробництва молока в агрофірмі за 2001 - 2010 рр.

значення факторної ознаки (якості ґрунтів), а на осі ординат - значення результативної ознаки (урожайності).

Лінійні діаграми зручні для зображення кількох паралельних рядів з метою їх порівняння (наприклад, динаміки продуктивності корів і рівня годівлі або інших якісно відмінних ознак). У цьому разі будують дві (при двох ознаках) або кілька шкал. Другу шкалу будують праворуч.

Особливе місце мають лінійні діаграми зі спеціальними базовими лініями. Найбільш типовими є два випадки. В першому випадку значення вертикальної шкали на початку координат приймають за 100%, тобто лінія, що виходить з цієї точки, відображає рівень базисної величини, яка дорівнює 100%. Всі значення величин, які перевищують базисну, розташовують вище цієї лінії, а значення, які менш рівня базисної величини, розташовують нижче.

У другому випадку при зображенні відхилень від середнього значення рівня (частіше у процентах) базова лінія, що характеризує середній рівень, є нульовою. Додатні відхилення (перевищення) від середнього рівня відкладають вище цієї лінії, від'ємні - нижче.

Діаграми у вигляді вертикальних стовпчиків і стрічок є найбільш простими і досить ефективними для аналізу соціально - економічних явищ видом графічного зображення.

Стовпчикові та стрічкові діаграми переважно застосовуються для порівняння різних показників у просторі і у часі, а також аналізу структури явищ.

Стовпчикові діаграми - це графіки, в яких різні величини представлені у вигляді стовпчиків однакової ширини, які розташовані один від одного на однаковій відстані або щільно. Якщо стовпчики розташовані не по вертикалі, а по горизонталі, то такі діаграми називаються стрічковими.

Основа порівняння в стовпчикових і стрічкових діаграмах - лінійна (одномірна). Висота стовпчиків і довжина стрічок відповідно з прийнятим масштабом пропорційна величині зображуваних явищ.

При побудові стовпчикових (стрічкових) діаграм потрібно додержуватись таких основних правил. Основи стовпчиків (стрічок) повинні бути рівними. Стовпчики (стрічки) можуть бути розміщені на однаковій відстані один від одного або щільно. Звичайно додержуються правила, щоб ширина проміжків була вдвоє меншою за ширину самих стовпчиків (стрічок). Висота стовпчиків і довжина стрічок повинні строго відповідати зображуваним цифрам.

Рекомендується включення в діаграму масштабної шкали, яка дає змогу визначити висоту стовпчика і довжину стрічки. Шкала може співпадати з гранню першого стовпчика або стрічки або розташовуватися на окремій лінії зліва (в стовпчиковій діаграмі) або у верхній частині (в стрічковій діаграмі). Шкала, на якій встановлюється висота стовпчиків або довжина стрічок повинна бути безперервною і починатися з нуля. Написи і вказівки цифр в кінці стовпчиків (стрічок) робити не рекомендується, бо це може створити зореве подовження стовпчиків (стрічок). Цифри показників краще всього писати всередині стовпчиків (стрічок), або розташувати в один ряд над ними на рівні закінчення шкали по осі ординат.

Стовпчики (стрічки) для кращої наочності можуть бути зафарбовані суцільною фарбою, якщо стовпчик (стрічка) відображає ціле явище, або кількома фарбами, якщо зображуються порівняння різних структур явищ, кожному з яких відведена частина стовпчика (стрічки).

Стрічковою діаграмою можна зображувати те саме що й стовпчиковою. Однак вертикальні стовпчики краще стрічок, якщо числа виражають ідею висоти (рівень зростання) і якщо невеликі пояснювальні написи до кожного стовпчика. Горизонтальні стрічки наочніше, якщо зображувані величини виражають ідею подовженості (автомобільних доріг, річок і т.п.) і якщо пояснювальний текст до них невеликий.

Стовпчикові і стрічкові діаграми краще за лінійні передусім у тих випадках, коли порівнюваних величин не так багато, порушується безперервність у часі (порівнюють не суміжні періоди) і потрібно звернути увагу не на відносну зміну, а на абсолютну величину порівнюваних рівнів.

Порядок побудови стовпчикової діаграми покажемо на такому прикладі (табл. 12.2).

Таблиця 12.2. Посівні площі сільськогосподарських культур в TOB району за 2009 і 2010 рр., тис. га

Порівняємо за допомогою стовпчикової діаграми загальну посівну площу в TOB району за 2009 і 2010 рр., яка відповідно становила 55,0 і 60,0 тис. га.

Для цього на осі абсцис побудуємо два стовпчика з основами по 3 см на відстані 1 см один від одного. Масштаб на осі ординат візьмемо рівним такому співвідношенню: 10 тис. га на 1 см. Цифри, що характеризують загальний розмір посівної площі, напишемо в середині стовпчиків. Для наочності стовпчики рекомендується зафарбувати або заштрихувати.

Побудуємо стовпчикову діаграму (рис. 12.2).

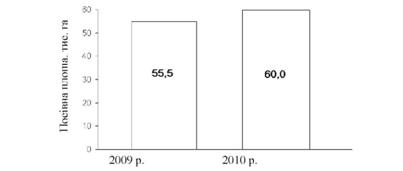
Рис. 12.2. Посівні площі в TOB району за 2009 і 2010 рр.

Стовпчикова діаграма може бути використана не тільки для характеристики загального розміру, а й структури того або іншого явища. При

побудові стовпчикової структурної діаграми висоту стовпчика беруть за 100% і поділяють на частини пропорційно структурі явищ (табл. 12.3).

Таблиця 12.3. Структура посівних площ в TOB району за 2009 і 2010 рр.

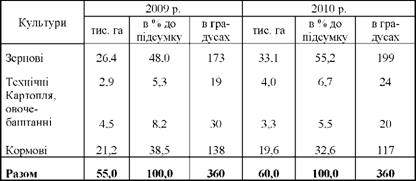
Щоб полегшити читання і аналіз таких діаграм, окремі складові частини розфарбовують різним кольором або штриховкою.

Використовуючи дані табл. 12.3, побудуємо стовпчикову структурну діаграму (рис. 12.3).

Під круговими (квадратними) діаграмами розуміють графіки, що виражають однорідні величини через площі кругів (квадратів).

Щоб побудувати кругову і квадратну діаграми з порівнюваних статистичних величин потрібно добути квадратні корені, а потім зобразити круги і квадрати із сторонами, пропорційними одержаним результатам.

Порівняємо між собою за 2010 р розмір посівних площ технічних (4,0 тис. га), картоплі і овоче-баштанних (3,3 тис. га) культур. Корені квадратні з посівних площ відповідно становлять =2,0 і ^/3,3 =1,8.

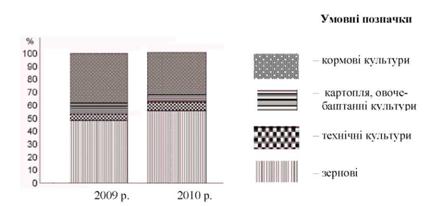
Рис. 12.3. Структура посівних площ в TOB району в 2009 і 2010 рр.

Якщо прийняти 1 см за 1 одиницю, то посівні площі можна зобразити або кругами з радіусами 2,0 і 1,8 см, або квадратами із сторонами 2,0 см для технічних культур і 1,8 см для картоплі і овоче-баштанних культур.

Побудуємо в прийнятому масштабі кругову і квадратну діаграми (рис. 12.4). На квадратних і кругових діаграмах на відміну від стовпчикових масштаб можна не наводити, але в кожній геометричній фігурі слід показати ті числові значення, які вони зображують.

Як видно з рис. 12.4, користуватися круговими і квадратними діаграмами для порівняння рівнів показників (розміру, обсягу) потрібно з обережністю, так як вони не дають точного уявлення про дійсні співвідношення порівнюваних величин і можуть навіть перекручувати уявлення про них. Це зумовлено тим, що візуально складно визначити, на скільки і у скільки разів одна фігура більша або менша за іншу. Крім того,

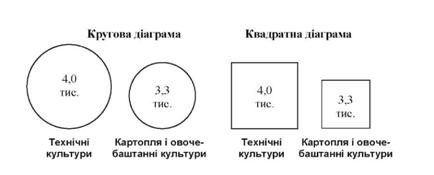
Рис. 12.4. Посівні площі технічних, картоплі і овоче-баштанних культур в TOB району в 2010 р.

той хто читає діаграму по-різному її сприймає, беручи за порівняння або висоту фігури, або її площу.

У зв'язку з цим перевагу слід віддавати здебільшого одномірним (лінійним) порівнянням, використовуючи для цих цілей стовпчикові або стрічкові діаграми.

Секторна діаграма являє собою круг, розділений радіусами на окремі сектори, кожний з яких характеризує питому вагу відповідної частини в загальному обсязі зображуваної величини. Секторні діаграми використовуються переважно для характеристики структури явищ. При порівнянні різних структур загальні площі кіл беруть однаковими. Кожний сектор виділяють за кольором або штриховкою; крім того в кожному секторі нерідко дають і цифрове позначення його питомої ваги. При малому куті сектора експлікація до нього вказується стрілкою.

При побудові секторної діаграми коло поділяють на сектори, площі яких пропорційні часткам частин досліджуваного явища. Площа круга зображує загальний розмір явища і беруть її такою, що дорівнює 100% або 3600. Перед побудовою діаграми абсолютні величини переводять у проценти, а проценти в градуси. Кожен процент дорівнює 3,6° (360:100).

Послідовність розміщення секторів визначається їхньою величиною: самий великий розміщується зверху, а решта - за рухом годинникової стрілки в порядку зменшення.

В секторній діаграмі можна в основний круг вписати малий круг, вказавши в ньому базу, рівну 100%.

Інколи замість круга використовують напівкруги, поділені на сектори, де 1% дорівнює 1,80.

Секторні діаграми наочні тільки тоді, коли досліджувана сукупність поділяється не більш як на 4 - 5 секторів і спостерігається значна структурна диференціація. Якщо сукупність поділяється на більшу кількість секторів і структурна диференціація незначна, то для зображення структури явищ доцільно застосовувати стовпчикову або стрічкову діаграму.

Побудову секторної діаграми покажемо на прикладі даних табл. 12.3. Для побудови секторної діаграми використаємо дані цієї таблиці і умовні позначки рис. 12.3. За допомогою транспортира знайдемо потрібні кути і поділимо однакові круги на сектори. Для кращої наочності графіка сектори круга зобразимо різною штриховкою (рис. 12.5).

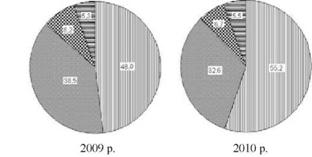
Рис. 12.5. Структура посівних площ в TOB району в 2009 і 2010 рр.

Радіальні діаграми використовуються для зображення явищ, які періодично змінюються у часі (переважно сезонних коливань). Для побудови їх використовують полярну систему координат. Круг поділяється на 12 рівних частин, кожна з яких означає певний місяць. Величину радіуса беруть за середньомісячний рівень (100%) і відповідно до цього масштабу на променях, починаючи від центра круга, відкладають відрізки, що зображують місячні рівні. Кінці цих відрізків з'єднують між собою, внаслідок чого утворюється замкнена фігура дванадцятикутник, який характеризує сезонні коливання досліджуваного явища.

В радіальній діаграмі за ось абсцис беруть коло, а за ось ординат - його радіуси, які є носіями масштабної шкали з точкою відліку від центра кола.

Залежно від того, який зображується цикл досліджуваного явища - замкнений або продовжуваний (з періоду в період) - розрізняють замкнені і спіральні радіальні діаграми. Наприклад, якщо зображуються дані по місяцях за кілька років, то при з'єднанні рівня грудня даного року з рівнем січня цього ж року діаграма буде замкненою; при з'єднанні рівня грудня даного року з рівнем січня наступного року утвориться спіральна діаграма. Спіральна діаграма застосовується в тому разі, якщо поряд з сезонними коливаннями відбувається систематичне зростання досліджуваного явища.

Проілюструємо побудову замкненої радіальної діаграми на такому прикладі (табл. 12.4).

Визначимо середній рівень ряду динаміки - середньомісячне виробництво молока:

Таблиця 12.4. Виробництво молока в агрофірмі по місяцях 2010 р.

Розрахуємо показники сезонності як відношення рівня кожного місяця в процентах до середньомісячного. Наприклад, для січня (1526 : 2000) -100 = 76,3%, для лютого (1616 : 2000) o 100 = 80,8% і т.д.

Обчислимо довжину радіуса для кожного місяця, прийнявши середньомісячний рівень рівним 3 см. Тоді величина радіуса для січня становитиме (3 -76,3) : 100 = 2,3 см, для лютого - (3 -80,8) : 100 = 2,4 см і т.д.

Графік показує, що найбільше виробництво молока спостерігається в травні - серпні, а найменше - в грудні - березні.

Побудуємо радіальну діаграму (рис. 12.6).

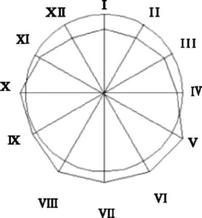
Рис. 12.6. Сезонність виробництва молока в агрофірмі

Особливою різновидністю площинних діаграм є графічні статистичні знаки, запропоновані російським статистиком В.Є. Варзаром (1851 - 1940 рр.). Знак Варзара являє собою площинну діаграму у вигляді прямокутника. Цей вид діаграм використовують для зображення показників, які є результатом перемноження двох інших пов'язаних між собою показників - факторів.

Застосування знаків Варзара ефективно для аналізу показників валового виробництва за складаючими (в рослинництві - через урожайність і площу, в тваринництві - продуктивність однієї голови і поголів'я) та інших складних показників з виявленням ролі окремих факторів. Так, наприклад, за допомогою знаків Варзара можна графічно зобразити динамічні і територіальні зміни таких показників як валовий збір сільськогосподарських культур (добуток урожайності на посівну площу), валова продукція (добуток продуктивності праці - виробництво продукції на одного працівника - на чисельність працівників), обсяг вантажоперевезень (добуток виробітку на одну автомашину на середньоспискову чисельність автомашин) тощо.

Знак Варзара будують у вигляді прямокутника, основа і висота якого визначаються за масштабом двома факторами - співмножниками, а площа - величиною результативного показника - добутка. Побудову знака Варзара (рис. 12.7) розглянемо на такому прикладі (табл. 12.5).

Таблиця 12.5. Поголів'я, продуктивність корів і валовий надій молока в TOB

Для побудови діаграми приймемо такий масштаб: на осі ординат (надій на корову) 10 ц на 1 см, по осі абсцис (середньорічне поголів'я) - 100 голів на 1 см.

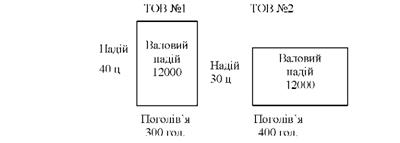
Рис. 12.7. Поголів'я, продуктивність корів і валовий надій молока в TOB

Як видно з рис. 12.7., валовий надій молока в двох TOB однаковий, але в TOB №1 його одержали від меншого поголів'я за рахунок більш високої продуктивності корів.

Лінійні напівлогарифмічні діаграми (графіки відношень) будують таким чином, щоб одна із шкал позначалась як логарифмічна, а друга - як арифметична. В даному випадку логарифмічний масштаб наносять на осі

ординат, а на осі абсцис розташовують рівномірну (арифметичну) шкалу для відліку часу за прийнятими інтервалами (роки, місяці, дні і т.д.).

Логарифмічний масштаб характерний тим, що в ньому відрізки шкали пропорційні не зображуваним числовим величинам, а їх логарифмам.

Напівлогарифмічні діаграми доцільно і ефективно застосовувати для порівняння відносних змін в динамічних рядах з істотно різними абсолютними рівнями. Цей вид діаграм має особливу цінність для зображення пропорційних і процентних відношень, оскільки на цьому графіку кут нахилу кривої виражає відносні зміни, наприклад темпів зростання.

Різниці ординат точок кривої (їх приріст) пропорційні темпам зростання, так само як і на звичайній шкалі ці ординати пропорційні рівням ряду. Отже, за логарифмічною шкалою можна визначити процентне відношення між будь-якими її точками.

Перевага напівлогарифмічних діаграм в аналізі рядів динаміки полягає в тому, що вони дають більш правильне уявлення про темпи динаміки. Тому лінійні напівлогарифмічні діаграми ще називають діаграмами темпів. Діаграма з рівномірною арифметичною шкалою правильно передає абсолютні прирости обсягів того або іншого явища, а відносні прирости (темпи) спотворює. Так, якщо виробництво продукції зростає рівномірно, збільшуючись з року в рік, наприклад, на 3%, то це означає, що абсолютні річні прирости будуть весь час збільшуватися. На рівномірній координатній сітці лінія динаміки матиме вигляд зростаючої кривої, а на напівлогарифмічній - вид прямої. Напівлогарифмічний графік правильніше покаже темпи зміни досліджуваного явища, що має велике значення для аналізу динаміки, особливо за тривалий період.

Проілюструємо це на такому прикладі. На рис. 12.8 зображено зростання урожайності кукурудзи на зерно в 2010 р. порівняно з 2002 р. двох підприємств: підприємства №1 з 20 до 30 ц/га і підприємства №2 -з 40 до 60 ц/га.

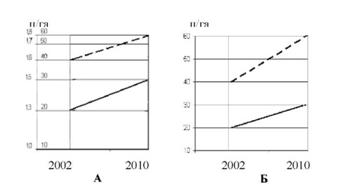
Рис. 12.8. Напівлогарифмічна (А) і арифметична (Б) лінійні діаграми динаміки урожайності кукурудзи на зерно

В обох підприємствах однаковий темп зростання урожайності, тобто збільшення в 1,5 рази, що уловлюється напівлогарифмічною діаграмою (рис. 12.8, А) без розрахунку відносних величин, а на арифметичній діаграмі (рис. 12.8, Б) на напрям ліній впливає величина абсолютного приросту (у підприємства №1 зростання урожайності становить 10 ц/га, а у підприємства №2 - 20 ц/га).

Техніка побудови логарифмічної шкали така (рис. 12.9).

Рис. 12.9. Логарифмічна шкала

Спочатку потрібно знайти логарифми вихідних чисел, накреслити ординату і поділити її на кілька рівних частин. Потім нанести на ординату (або рівну їй паралельну лінію) відрізки, пропорційні абсолютним приростам цих логарифмів.

Далі записати відповідні логарифми чисел і їх антилогарифми, наприклад 0,0000; 0,3010; 0,4771; 0,6021; ...; 1,0000, що дає 1, 2, 3, 4, 10. Одержані антилогарифми дають кінцевий вид шуканої шкали на ординаті. На логарифмічній шкалі немає нульової базової лінії, так як ^ 0 є - <ю.

Наведемо приклад побудови напівлогарифмічної діаграми. Припустимо, що потрібно зобразити на графіку рівень енергозабезпеченості підприємства за 1980 - 2010 рр. За ці роки вона зросла в 3,3 рази. Знайдемо логарифми для кожного рівня динамічного ряду (табл. 12.6).

Обчисливши мінімальне і максимальне значення логарифмів енергозабезпеченості, побудуємо масштаб з таким розрахунком, щоб усі дані розташувались на графіку

Таблиця 12.6. Динаміка енергозабезпеченості підприємства за 1980 - 2010 рр.

Враховуючи масштаб, знайдемо відповідні точки, які з'єднаємо прямими лініями, внаслідок одержимо графік (рис. 12.9) з використанням логарифмічного масштабу на осі ординат. Він називається діаграмою на напівлогарифмічній сітці.

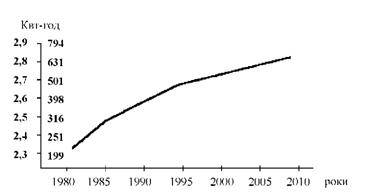
Таблиця 12.6. Динаміка енергозабезпеченості підприємства за 1980 - 2010 рр.

Повною логарифмічною діаграмою він стане в тому випадку, якщо на осі абсцис буде побудований логарифмічний масштаб. В рядах динаміки це ніколи не застосовується, так як логарифмування часу втрачає всякий смисл.

Застосування логарифмічного масштабу дає змогу без будь-яких обчислень характеризувати динаміку явища. Якщо крива на логарифмічному масштабі дещо відхилена від прямої і стає угнутою до осі абсцис, значить, має місце зниження темпів; коли крива наближається до прямої - стабільність темпів; якщо вона відхиляється від прямої в сторону, опуклу до осі абсцис (як в нашому прикладі), досліджуване явище (енергозабезпеченість) має тенденцію до зростання із зростаючими темпами.

Напівлогарифмічні діаграми широко використовуються при зображені відносних змін величин, виражених в різних одиницях вимірювання. Це дає змогу на одній діаграмі порівнювати темпи зростання середньої заробітної плати, продуктивності праці, випуску продукції та інші показники.

У цьому разі логарифмічна шкала поділяється на декілька циклів. Цифри кожного циклу в 10 разів більше цифр нижчого циклу. Наприклад, в межах нижчого циклу значення показника змінюються від 1 до 10, другого від 10 до

100 і т.д. Кожен цикл відповідає зміні характеристики логарифма на одиницю. Для побудови логарифмічної шкали потрібно масштаб циклу (наприклад, один цикл дорівнює 5 см) помножити на логарифми чисел від 1 до 10 і одержані добутки нанести на вертикальну шкалу в межах кожного циклу. Число самих циклів визначається амплітудою коливання рівнів (різницею між максимальним і мінімальним значенням).

Найвиразнішими і такими, що легко сприймаються, є зображувальні (картинні, фігурні діаграми), на яких дають художнє зображення будь-якого явища. Геометричні знаки (точки, лінії і т.п.) в зображувальних діаграмах замінюються фігурами, що якоюсь мірою символізують зовнішній образ зображуваного на графіку явища. Наприклад, поголів'я корів, свиней, овець в господарстві або господарствах району (області, країни) може бути зображено рядом фігур цих тварин.

Достоїнство таких графіків полягає у високому ступені наочності, в одержанні найкращого відображення порівнюваних явищ. Фігурні діаграми можуть бути побудовані за двома основними принципами: кількісному і пропорційному. Для кількісного діаграмування характерне використання рівних за розміром фігур - знаків, число яких показує величину зображуваних явищ.

Фігури, що зображують ту чи іншу величину, розташовують зліва направо на однаковій відстані. В цьому відношенні фігурні діаграми є різновидом лінійних діаграм, в яких поєднуються позитивні сторони стовпчикових і стрічкових діаграм і переваги символічного зображення порівняно з геометричним.

При побудові фігурних діаграм кожній фігурі надається конкретне числове значення і певні стандартні розміри. Сама ж досліджувана статистична величина зображується певною кількістю однакових за розміром фігур. Однак здебільшого не вдається зобразити статистичний показник цілою кількістю фігур. Останню з них доводиться ділити на частини, так як за масштабом один знак є занадто великою одиницею вимірювання. Складність її визначення є недоліком фігурних діаграм. Проте велика точність зображення статистичних даних у фігурних діаграмах не вимагається, і результати здержуються цілком задовільними.

Принцип пропорційної побудови фігурних діаграм ґрунтується на відображені величини порівнюваних показників розміром фігур у відповідній пропорції із зображуваними явищами. Недоліки цього способу, по суті, повторюють недоліки розглянутих вище кругових і квадратних діаграм. Внаслідок можливого досить значного перекручування при сприйнятті у виняткових випадках.

Покажемо приклад побудови фігурної діаграми за даними про чисельність фермерських господарств у двох областях (умовно А і Б) в 2010 р.

Рис. 12.10. Чисельність фермерських господарств у двох областях в 2010 р.

Приймемо умовно за один фігуро-знак 500 господарств. Тоді число фермерських господарств в області А в кількості 2550 буде зображено 5,1 фігурами, а в області Б в кількості 3250 - 6,5 фігурами.

Особливе місце в системі графічних зображень звітних і планових даних займають контрольно-планові графіки. Основне завдання цих графіків оперативна характеристика виконання тих або інших виробничих процесів і їх відповідність плановим завданням. Великою перевагою контрольно-планових графіків є те, що вони дають змогу наочного порівняння виконання плану по великому колу взаємопов'язаних об'єктів (бригад, ланок, видів робіт і т.д.).

Контрольно-планові графіки бувають різних видів і ступеня складності залежно від числа об'єктів і кількості ознак, що підлягають графічному зображенню.

Серед великого різноманіття контрольно-планових графіків для вивчення ходу виконання плану найчастіше використовують графік Ганта. Цей вид графіка зображує рівень виконання плану по кількох об'єктах як за окремі періоди, так і за звітний період в цілому.

Порядок побудови контрольно-планового графіка (графіка Ганта) розглянемо на такому прикладі (табл. 12.7).

Таблиця 12.7. Дані про хід сівби озимої пшениці по двох відділеннях агрофірми

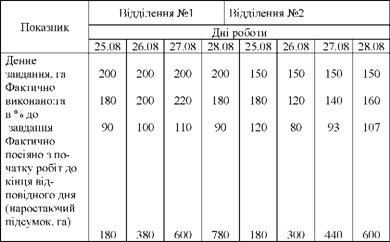
Цей графік побудуємо на спеціально розграфленій сітці, в якій по горизонталі в певному масштабі відкладемо періоди часу (дні), а по вертикалі вкажемо об'єкти спостереження .

Кожний відрізок по горизонталі, який означає відрізок часу (день), приймемо рівним 100% і поділимо його на 5 рівних частин, кожна з яких дорівнює 20% планового завдання. На графіку цю шкалу дамо зростаючим підсумком. При цьому позначки 0 і 100%, щоб не ускладнювати графік не даватимемо.

Ступінь виконання плану на графіку зобразимо двома лініями: тонкою і жирною. Тонка лінія покаже ступінь виконання плану за весь минулий період. Жирна лінія є своєрідною сумарною лінією, що характеризує ступінь виконання плану за станом на кожен день.

Побудуємо контрольно-плановий графік (рис. 12.11).

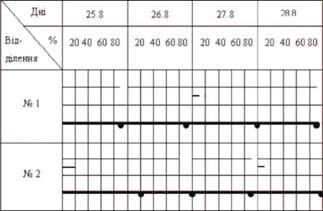
Рис. 12.11. Графік виконання плану сівби озимої пшениці по відділеннях агрофірми

Побудову графіка почнемо з даних по першому відділенню. Планове завдання першого дня (25.08) виконано на 90%. Відповідно до цього показника на діаграмі проведемо тонку лінію, яка займає 90% всього денного проміжку, або 4,5 поділки. За другій день (26.08) план виконано на 100%. Відповідно проведемо тонку лінію, яка займає весь денний відрізок (100%). Планове завдання третього дня (27.08) виконано на 110%. Тому тонка лінія займе всі п'ять частин денного відрізку (100%), під лінією в першій частині проведемо додатковий відрізок, який дорівнює половині першої частини (10%). Ця додаткова лінія показує перевиконання плану за третій день на 10%. За четвертий день (28.08) план сівби виконано на 90%. На діаграмі проведемо тонку лінію, яка займає чотири частини денного відрізку (80%) і половину останньої п'ятої частини, що становить 10% планового завдання.

Нанесемо на графік жирну лінію. На ній одночасно з її побудовою зробимо позначки про щодобове виконання плану. За перший день її довжина буде дорівнювати довжині тонкої лінії (90%). За другий день план виконано на 100%, а за перший і другий день сумарний процент становитиме 190% (90 + 100), тобто жирну лінію за перший день доведемо до 100%, а за другий день - до поділки, що відповідає 90%. Жирна лінія показує, що за перші два дні план не виконано на 10%, або на 20 га (400-380). За третій день план виконано на 110%, а за три дні разом сумарний процент становитиме 300% (90+100+110). Жирна лінія займе три повних денних відрізки. За четвертий день план сівби виконано на 90%. Відповідно сумарний процент за 4 дні становитиме 390% (90+100+110+90). Жирну лінію за четвертий день продовжимо до відмітки 90%.

Аналогічно нанесемо тонку і жирну лінії відповідно до даних відділення №2.

Аналіз контрольно-планового графіку показує, що за перші чотири дні посівних робіт відділення №1 не виконало план на 10%, або на 20 га (800-780), а відділення №2 виконало планове завдання на 100%.

До статистичних карт відносять картограми і картодіаграми. Для характеристики територіального розміщення яких-небудь соціально-економічних явищ (щільність населення по регіонах країни, розподіл районів за рівнем урожайності, продуктивності тварин і т.д.) застосовують картограми.

Картограма являє собою схематичну географічну карту, на якій різною фарбою або штриховкою зображено розподіл будь-якого явища в межах зображуваної на карті території.

Картограми можуть бути виконані по матеріалах окремого господарства (внутрішньогосподарський розріз по бригадах, відділках, полях сівозміни), району (в розрізі господарств), області (в розрізі районів) і т.д.

Картограми поділяють на фонові і точкові. Фонова картограма - вид картограми, на якій штриховкою різної густоти або фарбою різного ступеня насиченості зображають інтенсивність якого-небудь показника в межах територіальної одиниці. Цей вид картограм, як правило, використовується для зображення середніх і відносних показників.

При побудові фонових картограм попередньо здійснюється групування даних за досліджуваною ознакою. При цьому звичайно виділяють невелику кількість груп (не більше 5-6), а для наочності інтервали закруглюють. Для кожної групи встановлюються своя штриховка (інтенсивність її повинна зростати по мірі зростання показника). Група господарств (район), що попадають в той або інший інтервал, позначається на карті відповідною штриховкою.

Точкова діаграма - вид картограми, на якій рівень досліджуваного показника зображується за допомогою точок. Точки зображують одну одиницю сукупності або деяку їх кількість, показуючи на географічній карті щільність або частоту появи певної ознаки. Цей вид картограм використовується здебільшого для відображення розміщення і концентрації абсолютних показників - площі угідь, посівів, чисельності худоби і т.д. При цьому розмір того або іншого показника по територіальних одиницях характеризується певною кількістю точок.

При побудові точкової діаграми всі точки, що наносяться на карту, повинні мати однаковий розмір, так як кожна з них характеризує певну величину. Точки легко підрахувати на карті. Необхідно продумати, яку величину буде означати кожна точка; якщо це дуже мале значення, то потрібна буде дуже велика кількість точок, і, навпаки, мала кількість точок не дасть враження густоти.

Побудуємо точкову картограму розміщення посівів цукрових буряків в південній підзоні області (рис. 12.12).

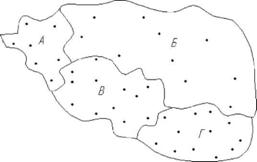
Рис. 12.12. Точкова картограма розміщення посівів цукрових буряків по районах південної підзони області

Точкова діаграма побудована за такими даними щодо площі посіву цукрових буряків: в районі А - 3500 га, Б - 5000, В - 6000, Г - 8000 га. Масштаб виражено таким співвідношенням: 1 точка дорівнює 500 га. Відповідно кількість точок по районам становитиме: А - 7 точок, Б - 10, В - 12, Г - 16 точок.

Загальним недоліком картограм є те, що в межах виділеної територіальної дільниці коливання статистичних показників чітко не вловлюється. Крім того, недоцільно зображувати абсолютні величини, так як вони відносяться до різних за величиною територій.

Картодіаграма - це поєднання схематичної географічної карти з однією з розглянутих вище діаграм (круговою, квадратною, стовпчиковою та ін.). Прикладом картодіаграм є географічна карта, на якій чисельність великих міст зображена у вигляді кіл різної величини.