Фінансовий менеджмент - Крамаренко Г.О. - 6.4.2.2. Змістовна інтерпретація невласних задач лінійного програмування

У моделі лінійного програмування, поставленій відповідно до реальної виробничо-економічної задачі, несумісність системи обмежень - явище досить звичне. Найчастіше коригування вектора Ь за рахунок прирощення АЬ приводить до розв'язуваності задачі (6.7). В основу коригування вектора можуть бути покладені різні підходи, які приводять до різних математичних постановок. Можна, наприклад, вимагати від коригуючого прирощення АЬ, щоб воно було аргументом оптимізаційної задачі

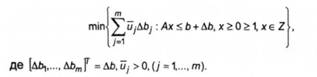
При цьому и~і можна інтерпретувати як міру втрат, пов'язаних зі зміною ресурсу АЬ на одиницю. За змістом описаного коригування деякі прирощення АЬ можуть бути від'ємними, І тоді у функції сумарних втрат відповідні до них доданки й,дЬ; будуть від'ємними.

Дещо інакшим, але змістовно очевидним виступає коригування, підпорядковане оптимізаційний задачі

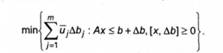
Розглянута інтерпретація невласності 1-го роду для задачі І пов'язана з ресурсним дефіцитом. Коригування такої задачі називають коригуванням за дефіцитом ресурсів. Однак причиною несумісності може бути просто неточність задання вектора Ь, бо майже всі економічні показники носять наближений характер.

Аналогічно інтерпретацію невласності 2-го роду для задач і пов'язують з неточністю інформації моделі. Причиною несумісності виявляється помилка у заданні вектора с.

Інтерпретація невласних задач лінійного програмування 3-го роду цікава тим, що вона двоїсто симетрична. Для задачі і симетрична корекція має вигляд:

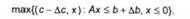
Піддавши аналогічному коригуванню задачу І*, одержимо

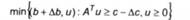
Нехай К = {[Ас, ДЬ] є Е^т: задача (6.18) розв'язувана},

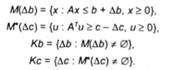
Очевидно, КЬ ф 0 і Кс * 0. Множини К, КЬ і Кс пов'язані співвідношенням К = КЬ o Кс.

Дійсно, одночасно сумісність систем

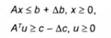
за деяких АЬ і Ас викликає розв'язуваність (6.18), а тому і (6.19). З іншого боку, якщо за деяких АЬ і Ас задача (6.18) розв'язувана, то розв'язувана і задача (6.19), а тому їхні системи обмежень (6.20) і (6.21) сумісні.

6.4.2.3. Моделі коригування невласних задач

Практика розв'язування виробничо-економічних задач фінансового планування підприємства показує, що виникнення невласних моделей системи - досить звичайна ситуація. Звичайно, виходячи з тих чи інших міркувань, можна ряд обмежень зняти або послабити, скоригувати вихідні дані і досягнути того, що задача буде розв'язуваною. Проте значно важливіший і доцільніший підхід, якій ґрунтується на застосуванні об'єктивних процедур для корекції такої моделі, тобто перетворення її на розв'язувану.

6.4.2.3.1. Модель прямої апроксимації

Запишемо задачу математичного програмування у вигляді

Зануримо її в сімейство параметричних задач:

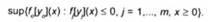
Тут (У0. У,."*. У,"} - система векторних параметрів, які належать до кінцевовимірних просторів. Це означає, що за певних значень цих параметрів ^§,у?.....у°}справедливі нерівності:

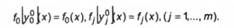
Покладаючи у = [у0, у,,..., yJ замість (6.22), можна використати запис

де а> 0.

Параметрична відносно Де є Япи ДЬ є Кт задача тах{(с-- Ас, х): Ах й Ь + ДЬ, х > 0} являє собою результат симетричного занурення задачі (6.1).

Більш загальна форма занурення задачі (6.1) у клас параметричних задач реалізується таким чином:

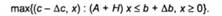
Нехай а - та або інша властивість задачі С (бути розв'язуваною, власною тощо).

Для (6.24) введемо множину Ко- {у: с(у) має властивість о}. Методи прямої апроксимації пов'язані з розв'язуванням задачі

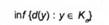
за того або іншого вибору критеріальної функції сУ(у). Наведемо приклади.

Нехай ст - властивість бути розв'язуваною для задачі

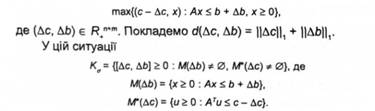
Сама задача апроксимації (6.23) зводиться до задач лінійного програмування:

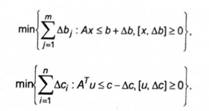
Розв'язком задачі відповідно до розглянутого прикладу виступає вектор |дс,дь],де Ас = (с-Атй}.г£=№-ьУ, х і й - оптимальні розв'язки задач (6.29) - (6.30) відповідно.

Функція сУ(Дс, ДЬ) може мати дещо загальніший вигляд:

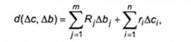
де Яу > 0, г, > 0 (у = 1,..., лл, /= 1,..., л). Тоді аналогами задач (6.29) і (6.30) будуть

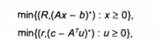
де Я = [/?,,..., /у, г= [г,,..., г^. Останні належать до класу випуклих кусково-лінійних задач математичного програмування.

6.4.2.3.2. Симетрична корекція задач лінійного програмування

Випишемо пару двоїстих задач лінійного програмування:

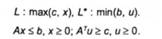
Розглянемо методи їх корекції за Ь і с. З цією метою задачам і і і* поставимо відповідно дві задачі

а) Лінійна корекція. Припустимо,

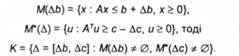
Зупинимося на аналізі задачі (6.32) при с/(Л) = ||Д||Г Легко переконатися в тому, що множину К, задану відповідно до (6.31), можна замінити на /<+ = {Д є К: А > 0}, не змінюючи оптимального значення задачі (6.32). Тим самим замість (6.32) можна розглядати задачу

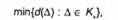
яка розпадається на дві самостійні:

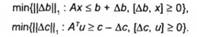
Задачі (6.33), (6.34) можна переписати так

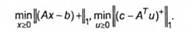
Візьмемо тепер у ролі сЦД) функцію

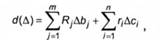
яка у змістовному значенні значно цікавіша. Тут Я. > 0, г > 0

(/= 1,..., т, і = 1.....л).

Аналогами задач (6.35) у цьому разі будуть

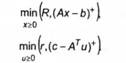
У питанні корекції і і І* задачі (6.36) і (6.37) проміжні: у результаті Тх розв'язання знаходяться відхилення дб = (Ах-ь)+ ■ де = Ір-Атйї"Дв х ' й - оптимальні розв'язки задач (6.36), (6.37). Кінцевою метою виступає розв'язання задач цд)і /_*{д), д = 1дс, дь|- У ряді випадків пошук д і розв'язання, наприклад, задачі цд) можна об'єднати в одну задачу. А саме: нехай £ - навласна задача 1-го роду, тоді де = о, і задачу цд) запишемо у вигляді

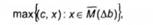
де щаь) - множина оптимальних розв'язків задачі (6.36), що еквівалентна задачі тахіс, х)-еф,(Ах-Ь)*йза достатньо великого

а > 0. Ця задача являє собою випуклу кусково-лінійну програму, її можна переписати як задачу лінійного програмування:

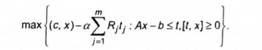
Якщо ж і - невласна задача 2-го роду, то дб = 0, і задачу /-*(д)запишемо у вигляді

р * ' - " '/

де м*(Ес) - множина оптимальних розв'язків (6.37), що еквівалентно задачі

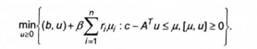
б) Квадратична корекція. Покладемо

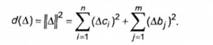
За схемою одержання задач (6.35) приходимо до задач

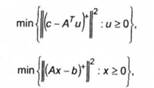
Побудуємо ітераційні оператори

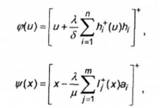
які мають властивості

хо, ио - довільні початкові елементи для процесів (6.40) і (6.41), х,й - оптимальні розв'язки задач (6.38) і (6.39). У теперішній час на підприємствах починають певною мірою використовувати методи оптимізації розвитку та розміщення виробництва. На окремих підприємствах розв'язання задач оптимізації знаходить своє застосування у рамках пошукових досліджень та епізодичного розв'язування окремих задач. Все більшого значення набуває можливість проведення багатоваріантних розрахунків на ЕОМ, що дозволяє проводити всебічний аналіз умов розвитку та розміщення виробництва на попередній стадії опрацювання фінансових планів.

Основним змістом економіко-математичних моделей задач поточного й перспективного фінансового планування в рамках підприємства виступає визначення оптимального рівня існуючих виробничих потужностей. Вони включають оптимальний розподіл ресурсів (у тому числі сировини) між різними підрозділами підприємства у встановлених межах. Однак треба визнати, що рівень досліджень у цій галузі поки що не забезпечив розробку єдиної системи задач оптимізації фінансового планування підприємства.

За допомогою економіко-математичних методів і систем моделей розв'язуються найрізноманітніші задачі перспективного фінансового планування. У напрямку вдосконалення такого роду моделей найбільш актуальні такі: по-перше, типізація задач і моделей, вироблення єдиних методичних положень про умови техніко-економічних розрахунків, створення нових ефективних методів і алгоритмів розв'язування задач на ЕОМ і, по-друге, конкретизація моделей методів і алгоритмів стосовно специфічних умов кожної розв'язуваної задачі розвитку і розміщення виробництва.