Економіка праці та соціально-трудові відносини - Гриньова B.M. - Запитання та завдання для самоконтролю

Прогнозуючи числові ряди, треба враховувати дисконтування вихідних даних. Очевидно, кінцевим точкам ряду потрібно надати більше значення, а спостереженням, які належать до минулого, — менше. Це можна частково врахувати за допомогою процедури ковзних середніх із кінцевою довжиною відрізка усереднення, де значення ваг, які приписують останній групі (2m+1), не залежать від попередніх значень.

Метод експоненціального згладжування є одним із головних. Він поєднує метод екстраполяції та кованої середньої і дає змогу побудувати такий опис прогнозованого процесу, в якому пізнішим спостереженням надають більшого значення порівняно з попередніми, причому значення спостережень спадають за експонентою.

Вихідний динамічний ряд можна записати у вигляді полінома:

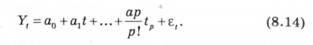
Для розрахунків за методом експоненціального згладжування вводять експоненціальну середню &-го порядку в],*',, яку визначають за формулою

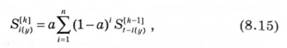
Важливу роль у методі експоненціонального згладжування відіграє вибір оптимального параметра згладжування а. Залежно від параметра а прогнозні оцінки по-різному враховують вплив зміни значення вихідного ряду спостереження: чим більше значення а, тим більший внесок останніх спостережень у формування тренда, а вплив початкових умов швидко послаблюється.

Адаптивне згладжування. Головною сферою застосування адаптивних методів прогнозування є отримання прогнозних результатів для показників, динаміку яких характеризує регулярна зміна. Вихідна інформація для використання адаптивних методів: динамічні ряди з кількістю спостережень не менше 10—15 точок. Результати отримують у вигляді числових значень динаміки ряду на перспективу, використовуючи лінійну адаптацію моделі:

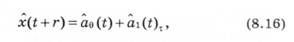
Метод найменших квадратів застосовують для відшукування наближених залежностей між двома або кількома прогнозованими величинами за їх емпіричним значенням. Суть його полягає у мінімізації суми квадратичних відхилень між спостережуваними величинами і відповідними оцінками (розрахунковими величинами), обчисленими за підібраним рівнянням.

У випадку апроксимування справжнього розвитку явища за допомогою поліноміального тренда залежну величину у можна записати як функцію часу у вигляді многочлена:

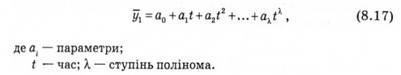
Оцінки параметрів а₀, а₁, a_y,можна отримати за допомогою методів найменших квадратів. Розгорнутий запис системи нормальних рівнянь, в якій змінні Х₀, Х₁, Х_m замінені характеристиками часу t, t²,... t, має такий вигляд:

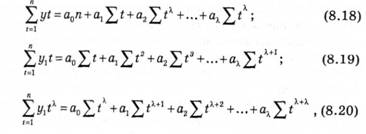
де n — кількість членів у динамічному ряду.

Використовуючи матричні позначення, цю систему можна записати у вигляді:

Отже, система, яка складається з λ-рівнянь, як відомі величини містить λ-невідомих величин аj. Розв'язок цієї системи стосовно а0, а1, aλ і дає значення параметрів, які відшукують.

Одним із головних методів прогнозування випадкової компоненти є метод авторегресії. Прогнозуючи деяку величину, природно допустити залежність її в довільний момент часу від значень у попередні моменти. Будь-який процес залежить від низки факторів. Модель прогнозування, побудована як функція від передісторії, повинна враховувати можливі дії цих факторів. Тоді досліджуваний процес можна записати так:

Модель є авторегресивною формою прогнозованого процесу. Головною умовою правомірності її застосування є випадковість і стаціонарність. Для отримання точніших оцінок схему авторегресії можна модифікувати на підставі застосування вагових коефіцієнтів.

Якщо ряди дуже довгі, то для виділення тренда використовують метод, що ґрунтується на переході від вихідної інформації до різниць того чи іншого порядку.

До методів спільного прогнозування трендової і випадкової складових динамічного ряду належить метод Бокса—Дженкінса. Безпосередньо модель Бокса—Дженкінса — це об'єднання двох форм подання вихідного динамічного ряду: авто-регресивного і ковзної середньої.

Для прогнозування багатовимірних процесів використовують методи багатофакторного прогнозування. Вони прості в реалізації, досить "м'які" щодо вимог до вихідної інформації і дають змогу отримати достовірні прогнозні результати.

Процедурні переваги методів передбачають чіткий вибір виду функціональної залежності пояснювальної змінної від часу і незалежних змінних. По суті, якість отриманих прогнозних результатів залежить, насамперед, від правильності вибору виду функціональної залежності й меншою мірою — від якості вихідної інформації.

Вихідною інформацією для отримання прогнозних результатів за допомогою методів багатофакторного прогнозування є матриця спостережень за часом залежної і незалежних змінних (тобто застосування матричного методу).

Кожний стовпчик цієї матриці — часовий ряд спостережень, упорядкований за часом. Для вихідної інформації мають виконуватися деякі головні передумови — такі як Т≥ 3—5, Т≥ 15— 20, Це означає, що кількість спостережень за кожним фактором має бути у 3—5 разів більшою від досліджуваних факторів, у всякому разі — не менше 15—20 спостережень.

Найпоширенішими є методи регресійного і кореляційного аналізів.

Регресійний аналіз використовують для дослідження форм зв'язку, які визначають кількісні співвідношення між випадковими величинами досліджуваного випадкового процесу. Регресійний аналіз є частиною теорії кореляції. Нехай

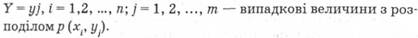
Регресією називають функцію

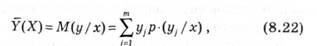
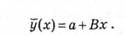
Коефіцієнти а і В обчислюють методом найменших, квадратів на підставі умови мінімізації функції помилки.

Для найскладніших процесів будують модель множинної лінійної регресії:

У цьому випадку, як і в простій функції, завдання зводиться до визначення коефіцієнтів 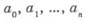шляхом мінімізації функції помилок.

Кореляційний аналіз визначає кореляційні зв'язки між випадковими величинами. Дві випадкові величини а і b називають кореляційно пов'язаними, якщо математичне сподівання однієї з них змінюється залежно від зміни іншої. Парна кореляція дає змогу з'ясувати залежність між двома показниками.

Якщо спостереження за одним показником 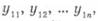а за іншим 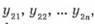, то коефіцієнти парної кореляції обчислюють за формулою

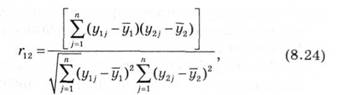
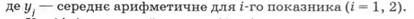
Коефіцієнт парної кореляції змінюється у межах від -1 до +1. Чим більше коефіцієнт наближається до +1, тим сильніший прямий зв'язок, чим ближче коефіцієнт до —1, тим сильніший обернений зв'язок між показниками. Із наближенням коефіцієнта до нуля зв'язок між показниками послаблюється.

Кореляційний аналіз дає змогу перевірити різні економічні гіпотези про наявність та силу зв'язку між двома явищами і групою явищ.

Світовою наукою і практикою відпрацьована і використовується така макроекономічна модель, як виробнича функція Кобба-Дуг ласа.

Виробнича функція Кобба-Дугласа розроблена американцями Ч. Коббом і П. Дугласом. її можна використати для визначення темпу зростання виробленого продукту (у). Обсяг випуску продукції (У) визначається, виходячи з наявних запасів факторів виробництва та ефективності їх використання. Як фактори виробництва розглядаються запаси праці (L) і капіталу (К). Ефективність використання факторів виробництва задається показниками граничної корисності при капіталі 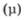і праці :

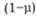Зв'язок між макроекономічними показниками для прогнозування зростання виражається у відносних показниках темпів зростання:

Спрогнозувавши величину приросту праці (і) та капіталу (в), можна визначити темп приросту виробленого продукту.

Найефективнішим засобом прогнозування, особливо довготермінового, є динамічні та ігрові імітаційні моделі. Перші дають змогу робити висновки про головні риси розвитку економічних систем, які суттєво не залежать від початкових умов. Ці висновки потрібно згодом деталізувати за допомогою Інших методів, наприклад, апарату математичного програмування.

У ситуації, коли відомі математичні методи і моделі виявляються надто спрощеними та не можуть адекватно відобразити економічну реальність, використовують також методи імітаційного моделювання.

Імітаційна модель є формалізованим описом виробничої системи через її елементи та залежності між ними, вона відображає порядок розрахунку показників, які характеризують ці елементи і залежності.

Складати прогнози можна, як уже зазначено, методами, що не є безпосередньо методами прогнозування. До них можна віднести варіаційне обчислення, теорію катастроф, описування розвитку системи за допомогою диференціальних рівнянь, сплайн-функцій.

Запитання та завдання для самоконтролю

1. У чому сутність моніторингу соціально-трудової сфери?

2. Які показники відображають моніторинг соціально-трудової сфери?

3. Визначте основні методи соціально-економічних досліджень.

4. У чому суть експертних методів?

5. Що таке метод Дельфі?

6. У чому особливості застосування методів екстраполяції?

7. Що можна проаналізувати за виробничою функцією Кобба-Дугласа?