Економічний аналіз діяльності підприємства - Савицька Г.В. - 1.6. Системи виміру впливу факторів у детермінованому аналізі.

Сутність, призначення і сфери застосування методів ланцюгової підстановки, абсолютних різниць, відносних різниць, пропорційного поділу, інтегрального методу і методу логарифмування.

Визначення величини впливу окремих факторів на приріст результативних показників - це одне із методологічних питань в аналізі. У детермінованому аналізі для цього застосовують такі методи: ланцюгової підстановки, абсолютних різниць, відносних різниць, пропорційного поділу, інтегральний метод, метод логарифмування, балансовий спосіб та інші.

Найбільш універсальний з них - метод ланцюгової підстановки. Його застосовують для розрахунку впливу факторів в усіх типах детермінованих факторних моделей: в адитивних, мультиплікативних, кратних і змішаних (комбінованих). Цей спосіб дає змогу визначати вплив окремих факторів на зміну величини результативного показника шляхом поступової заміни базисної величини кожного факторного показника в обсязі результативного показника на фактичну величину у звітному періоді. З цією метою визначають ряд умовних величин результативного показника, які враховують зміну одного, потім двох, трьох і наступних факторів, допускаючи, що інші не змінюються. Порівняння величини результативного показника до і після зміни рівня того чи іншого фактора дає змогу елімінувати вплив усіх факторів, крім одного, і визначити його вплив на приріст результативного показника.

Схематично це можна подати так:

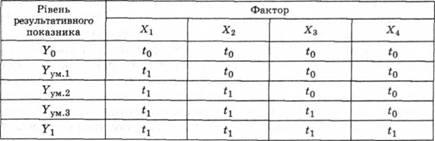
Примітка: (₀ - базове значення факторного показника (минулого періоду, плану, іншого підприємства); (, - поточний рівень факторного показника.

Загальна зміна результативного показника: АУ_заР = У і - У о o

У тому числі:

=Уум,2 ~^ум.1"

Балансова перевірка:

ДУааг =ДУ_Ж1 +ДУ*<.

Застосовуючи метод ланцюгової підстановки, необхідно дотримувати такої послідовності розрахунків: передусім потрібно враховувати зміни кількісних, а потім якісних показників. Якщо ж є кілька кількісних і кілька якісних показників, то спершу слід змінити величину факторів першого рівня підпорядкованості, а потім.нижчого. Згідно з рис. 1.2, чисельність працівників щодо валової продукції - фактор першого рівня, кількість відпрацьованих днів - фактор другого рівня, тривалість робочого дня і виробіток в середньому за годину - фактори третього рівня. У такій послідовності визначають їхній вплив на змінювання обсягу валової продукції.

Отже, застосування методу ланцюгової підстановки потребує знання взаємозв'язку факторів, співпідпорядкованості їх, уміння правильно класифікувати і систематизувати їх, тому що від порядку підстановки залежать результати розрахунків.

Спосіб абсолютних різниць застосовують для розрахунку впливу факторів на приріст результативного показника в детермінованому аналізі, але тільки в мультиплікативних моделях (У = Хі -х% **а -...-Хп) і моделях мультиплікативно-адитивного типу: У = (а - Ь) с і У=а (Ь - с). І хоча використання його обмежене, завдяки його простоті він широко застосовується в економічному аналізі.

Застосовуючи його, величину впливу факторів розраховують помноженням абсолютного приросту значення досліджуваного фактора на базовий рівень факторів, які стоять справа від нього, і на поточний рівень факторів, розташованих зліва від нього в моделі.

Алгоритм розрахунку для мультиплікативної чотирифактор-ної моделі валової продукції є таким:

ВП = ЧР Д Т ГВ;

ДВЛчр = Д7РД₀ -То -ГВоі

АВП_л=ЧР_гЬД-Т₀'ГВо;

АВП_Т =7і>і Ді *ДГГВ₀;

ДВЯ_гв=7і^>іДі-7^,₁.ДГВ.

За допомогою способу абсолютних різниць одержують ті самі результати, що й за допомогою способу ланцюгової підстановки. При цьому також необхідно пильнувати, щоб алгебраїчна сума приросту результативного показника за рахунок окремих факторів дорівнювала його загальному приросту.

Розглянемо алгоритм розрахунку факторів за цим способом у моделях мультиплікативно-адитивного виду. Для прикладу візьмемо факторну модель прибутку від реалізації продукції:

П=УРП(Ц-С),

де П - прибуток від реалізації продукції; УРП - обсяг реалізації продукції; Ц - ціна одиниці продукції; С - собівартість одиниці продукції.

Приріст суми прибутку за рахунок змін:

o обсягу реалізації продукції: АПурп =ДУРП(Цо -Со);

o ціни реалізації: ДЛц =УРП АЦ;

o собівартості продукції: АПс=УРП * (-ДС).

Спосіб відносних різниць застосовують для виміру впливу факторів на приріст результативного показника тільки в мультиплікативних моделях. При цьому використовують відносний приріст факторних показників, виражений коефіцієнтом або процентом.

Розглянемо методику розрахунку впливу факторів цим способом для мультиплікативних моделей типу У =а -Ь o с.

Зміни результативного показника визначають у такий спосіб:

ДУ₀=у" -

ДУ₆=(У₀+ДУ.)-ДУ_с=(У₀+ДУ_а+ДУ"). ^.

Со

За цим правилом для розрахунку впливу першого фактора необхідно помножити базову величину результативного показника на відносне приріст першого фактора, вираженого десятковим дробом.

Щоб розрахувати вплив другого фактора, потрібно до базової величини результативного показника додати зміну його за рахунок першого фактора, а потім знайдену суму помножити на відносний приріст другого фактора.

Вплив третього фактора визначають аналогічно: до базової величини результативного показника додають його приріст за рахунок першого і другого факторів і отриману суму помножують на відносний приріст третього фактора і т. д.

Спосіб відносних різниць зручно застосовувати тоді, коли потрібно розраховувати вплив великого комплексу факторів (8- 10 і більше). На відміну від попередніх способів тут значно скорочується число обчислювальних процедур, що зумовлює його перевагу.

Спосіб пропорційного поділу використовують тоді, коли мають справу з адитивними моделями У = ^ х і моделями кратно-адитивного типу;

у__а_. у_а+ь+с+...+л

Ь+с + сі + ...+п' к

В однорівневій моделі типу У =а+Ь+с алгоритм розрахунку впливу факторів буде таким:

^ДУ" - д л ^Аа'

Да+До+Дс

^АУ* ⁼ л ^а аГ а Да + До+Де

Да + Д& + Дс

У моделях кратно-адитивного виду спершу необхідно за методом ланцюгової підстановки визначити, наскільки змінився результативний показник за рахунок числівника і знаменника" а потім за способом пропорційного поділу зробити обрахунок впливу факторів другого порядку за наведеними вище алгоритмами.

Для розв'язання такого типу задач можна також використати спосіб часткової участі. Для цього спершу визначають частку кожного фактора в загальній сумі їхніх приростів, котру потім помножують на загальне зростання результативного показника:

ду ^Аа ДУ

^Уа-Аа + АЬ + Лс ^ДУзаг'

Да+До+Дс

ду = ^Ас ЛУ Да + Дб+Дс

Інтегральний метод застосовують для виміру впливу факторів у мультиплікативних, кратних і кратно-адитивних моделях. Застосування цього способу дає змогу отримати точніші результати розрахунку впливу факторів порівняно з методами ланцюгової підстановки, абсолютних і відносних різниць, оскільки додатковий приріст результативного показника від взаємодії факторів приєднується не до останнього фактора, а ділиться порівну між ними.

Розглянемо алгоритми розрахунку впливу факторів для різних моделей.

Д£г = Аху₀ +-|дхДу або А/* = ^Ах(у₀ Д/_у = Аух₀ +^АхАу або Afy =іду(яг₀ +*і). 2. і =хуг;

А/_х =^Ах(у₀*і +Уі*о)+хД*ДуАг; А1_У =-^Ау(х₀гі +Хіг₀)+-АхАуАг; Аи =^Аг(х₀уі +ХіУ₀)+-АхАуА2.

Для розрахунку впливу факторів у кратних і змішаних моделях використовують такі алгоритми.

1. Вид факторної моделі: '""¡7*

2. Вид факторної моделі: і =-;

^ + 2

а* Ах ,"ГУі +*і 1

А/* ^=_:-г" * ^ш- '

Ду+Дг 1_Уо+2о]

а* А/заг"Д^х _А".

^А'"⁼ Д_У+Д* ^ЛУ'

_{Д/я =}^А^г-А/х_Дг>

Ду + Дг

Якщо в знаменнику більше двох факторів, то процедуру продовжують. Отже, застосування інтегрального методу не потребує знання всіх процесів інтегрування. Достатньо у ці готові робочі формули підставити необхідні числові дані і зробити не дуже складні обчислення за допомогою калькулятора або іншої обчислювальної техніки.

Метод логарифмування застосовують для виміру впливу факторів у мультиплікативних моделях. Як і при інтегруванні тут теж результат розрахунку не залежить від розміщення факторів у моделі і, порівняно з інтегральним методом, забезпечується більш висока точність розрахунків. Якщо при інтегруванні додатковий приріст від взаємодії факторів розподіляється порівно між ними, то за допомогою логарифмування результат сумісної дії факторів розподіляють пропорційно до частки ізольованого впливу кожного фактора на рівень результативного фактора. У цьому його перевага, а недолік - в обмеженості сфери його застосування.

На відміну від інтегрального методу, при логарифмуванні цим способом використовують не абсолютні прирости показників, а індекси їхнього зростання (зниження).

Припустимо, що результативний показник можна подати як добуток трьох факторів: / = хуг. Вплив цих факторів визначають у такий спосіб:

Д/х = Д/заг -Г-Гі-7Т^;

1*(Л :/о)

_аі V - щ{уг :уо).

1в(Л:/о)

Із формул випливає, що загальний приріст результативного показника розподіляється за факторами пропорційних відношень логарифмів факторних індексів до логарифму індексу результативного показника. І не має значення, який логарифм використовують - натуральний чи десятковий. Перевага способу логарифмування полягає у відносній простоті обчислень і підвищенні точності розрахунків.

Сферу застосування прийомів детермінованого факторного аналізу в систематизованому вигляді можна подати як таку матрицю:

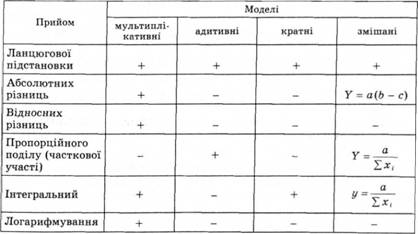
Знання суті цих прийомів, галузі застосування їх, процедури розрахунків - необхідна умова кваліфікованого проведення аналізу.