Обгрунтування господарських рішень та оцінювання ризиків - Донець Л.І. - 13.2. Розв'язання матричної гри в середовищі Macrosoft EXCEL

Для розв'язання ЗЛП можна використовувати середовище Microsoft EXCEL, який має вбудований оптимізаційний модуль "Поиск решения" (або "Пошук рішення" або "Solver" - назва залежить від мови інтерфейсу програми).

Приклад 13.2. Знайти рішення матричної гри, що було розглянуто в прикладі 13.1, за допомогою середовища Microsoft EXCEL.

Розв'язання. В першу чергу слід визначити структур моделі задачі на робочому листі:

Крок 1. Заповнити платіжну матрицю (рис. 13.1).

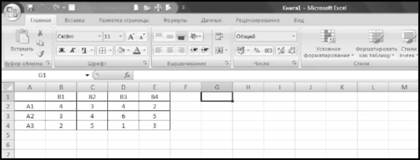
Рисунок 13.1 - Платіжна матриця гри на робочому листі EXCEL

Крок 2. Під платіжною матрицею слід задати блок змінних

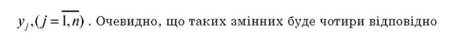
до кількості стратегій гравця В. Зважаючи на, що мова йде шукані змінні задачі, під час розв'язування програма буде змінювати їх значення. На підготовчому етапі слід визначити стартові довільні числа (наприклад, 0,01 для кожної змінної). Результати представлено на рис. 13.2.

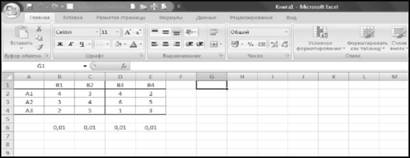
Рисунок 13.2 - Платіжна матриця гри зі стартовими значеннями задачі на робочому листі EXCEL

Крок 3. Слід задати формули лівих частин системи обмежень. Оскільки ліва частина кожної нерівності є сумою добутків елементів відповідного рядка, що відповідає стратегії гравця А, та стовпчика зі змінними у., то для її визначення можна скористатися стандартною функцією EXCEL, яка називається СУММПРОИЗВ. Покажемо як нею скористатись на прикладі першої нерівності системи обмежень.

Виберемо клітину G2 і у майстері функцій виберемо функцію СУММПРОИЗВ (рис.13.3).

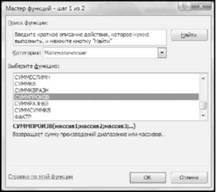
Рисунок 13.3 - Майстер функцій

Натиснемо кнопку "ОК" і з'явиться діалогове вікно, в якому задамо посилання: "Массив 1" - значення В2:Е2, "Массив 2" - значення В6:Е6 (рис.13.4).

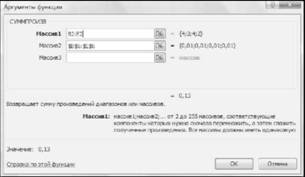
Рисунок 13.4 - Введення формули обмежень задачі

Слід відмітити, що адреси клітин, що записані у полі "Массив 2" доцільно зафіксувати з метою подальшого їх копіювання. Це можна зробить за допомогою кнопки Е4 - отримаємо $В$6:$Е$6.

Натиснемо кнопку "Ок" і в клітині G2 отримаємо результат -0,13. Копіюємо формули від G2 до G4 (рис. 13.5).

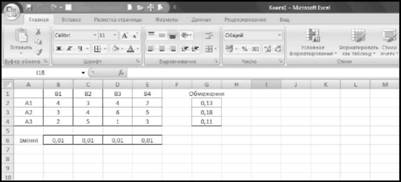
Рисунок 13.5 - Результат введення формул обмежень задачі на робочій лист EXCEL

Крок 4. Слід задати формулу цільової задачі, яка в нашому випадку є сумою змінних у. з протилежним знаком, яка підлягає мінімізації. Для цього можна скористатися стандартною функцією СУММ, встановити за аргумент адресу діапазону змінних: В6:Е6. Результат наведено на рис 13.6.

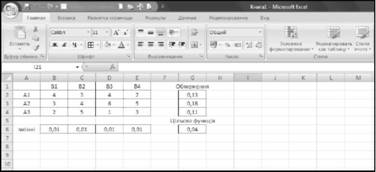
Рисунок 13.6 - Результат введення формули цільової функції задачі на робочій лист EXCEL

Крок 5. В меню "Сервис" обрати опцію "Поиск решения", в результаті чого з'явиться діалогове вікно "Поиск решения" (рис.13.7).

Якщо в меню "Сервис" пункту "Поиск решения" немає, тоді в меню "Сервис" слід обрати опцію "Надстройки". В діалоговому вікні, що з'явиться, необхідно вибрати зі списку доступних надбудов "Поиск решения" і натиснути кнопку "ОК". Після чого в меню "Сервис" з'явиться опція "Поиск решения".

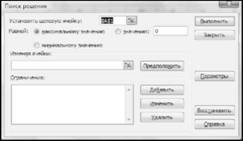
Рисунок 13.7 - Діалогове вікно "Поиск решения"

Крок 6. Постановка цільової функції. В діалоговому вікні "Поиск решения" в полі "Установить целевую ячейку" вказати адресу клітини на тому самому робочому листі, де було задано формулу цільової функції. В нашому прикладі це клітина $0$6 (формулу цільової функції було введено на кроці 4). Для завдання напряму оптимізації цільової функції виберемо опцію "минимальному значению" (рис. 13.8).

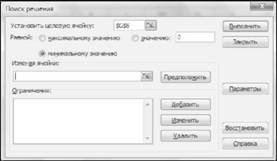
Рисунок 13.8 - Результат введення значення цільової функції в діалоговому вікні "Поиск решения"

Крок 7. Визначення діапазону змінних задачі. В діалоговому вікні "Поиск решения" в полі "Изменяя ячейки" вказати діапазон змінних задачі, що задані на робочому листі. В нашій задачі це $В$6:$Е$6 (рис. 13.9)/

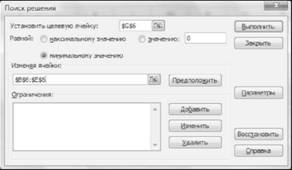
Рисунок 13.9 - Результат визначення діапазону змінних задачі в діалоговому вікні "Поиск решения"

Крок 8. Введення обмежень задачі. Формули обмежень були задані на кроці 3. Для того, щоб зареєструвати їх як обмеження оптимізаційної процедури і встановити їх тип потрібно натиснути кнопку "Добавить", при цьому діалогове вікно "Поиск решения" зникне, а з'явиться додаткове діалогове вікно "Добавление ограничения" (рис. 13.10).

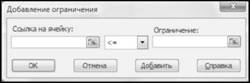
Рисунок 13.10 - Діалогове вікно "Добавление ограничения"

У діалоговому вікні "Добавление ограничения" слід зареєструвати всі обмеження, яких в нашій задачі три (без урахування обмежень на невід'ємність змінних, які задаються окремо).

У полі "Ссылка на ячейку" діалогового вікна "Добавление ограничения" слід задати адресу формули обмеження. Для першого обмеження це G2. Далі зі списку слід обрати тип обмеження. У нашому випадку це "<=".

У полі "Ограничение" слід записати значення правої частини обмеження. Для першого обмеження це число "1" (рис. 13.11).

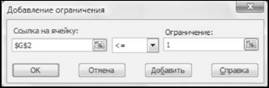
Рисунок 13.11 - Результати введення першого обмеження у діалоговому вікні "Добавление ограничения"

Після цього слід натиснути кнопку "Добавить" і обмеження буде зареєстроване. Аналогічно слід зареєструвати останні обмеження. На останньому кроці замість кнопки "Добавить" слід натиснути "ОК", коли більш не потрібно задавати нові обмеження.

Після цього повернемося до основного діалогового вікна "Поиск решения" (рис. 13.12).

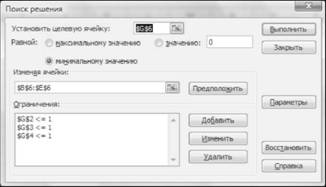
Рисунок 13.12 - Результати введення обмеження у діалоговому вікні "Поиск решения"

Крок 9. Введення обмежень на невід'ємність змінних задачі. У діалоговому вікні "Поиск решения" натиснути кнопку "Параметри" і в діалоговому вікні, що з'явиться, встановити галочку у опції "Неотрицательные значения". В цьому діалоговому вікні можна встановити галочку у опції "Линейная модель" (рис.13.13).

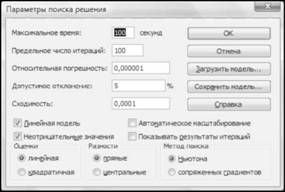
Рисунок 13.13 - Діалогове вікно "Параметры поиска решения"

Після цього слід натиснути кнопку "ОК" і вікно "Параметры поиска решения" зникне, а з'явиться діалогове вікно "Поиск решения".

Крок 10. Початок роз'язання оптимізаційної задачі. Потрібно натиснути кнопку "Выполнить". Отримаємо повідомлення, яке з'явиться у діалоговому вікні "Результаты поиска решения" (рис.13.14).

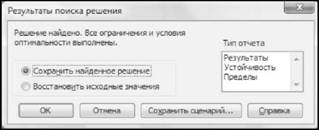
Рисунок 13.14 - Діалогове вікно "Результаты поиска решения"

Після отримання повідомлення слід натиснути кнопку "ОК" і на робочому листі EXCEL отримаємо рішення ЗЛП (рис. 13.15).

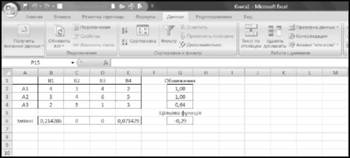
Рисунок 13.15 - Результати розв'язання ЗЛП на робочому листі EXCEL

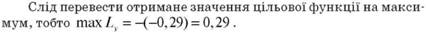
Крок 11. Обчислення ціни гри. Для цього потрібно за формулою

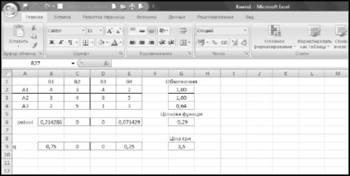
Рисунок 13.16 - Результати матричної гри на робочому листі EXCEL

Для визначення змішаної стратегії гравця А слід повторити всі кроки.

Таким чином, результати розв'язання матричної гри в середовищі Microsoft EXCEL і за допомогою зведення до пари взаємнодвоїстих задач, одну з яких розв'язано симплексним методом співпадають.

Питання для поточного контролю та поглибленого засвоєння знань

1. Запишіть задачу лінійного програмування, до якої може бити зведено матричну гру, з боку гравця А.

2. В чому полягає послідовність дій при розв'язанні матричної гри розміром m X n ?

3. В чому полягає сутність симплекс-методу?

4. На яких властивостях ЗЛП основується симплекс-метод?

5. Як ввести додаткові змінні в систему обмежень ЗЛП?

6. В якому випадку штучні змінні не слід вводити систему обмежень ЗЛП?

7. В чому полягає критерій оптимальності опорного плану?

8. Який стовпець називається розв'язувальним?

9. Який рядок називається розв'язувальним?

10. Що таке симплексне відношення оптимальності?

11. Що показує розв'язувальний рядок?

12. Де знаходиться генеральний елемент?

13. В чому полягають правила переходу до наступної симплекс-таблиці?

14. Як у симплекс-таблиці знайти опорний план?

15. За допомогою якої процедури в середовищі Масговоіі EXCEL можна знайти рішення ЗЛП?