Теорія ігор – розділ прикладної математики, який вивчає математичні моделі прийняття рішень у так званих конфліктних ситуаціях, що мають місце. Основоположниками теорії ігор є математик Дж. Фон Непман та економіст О. Моргенштерн. В подальшому її розвинули Неш Джон, Зелтен Райнхард, Харшаньї Джон Чарльз, які в 1994 р. стали лауреатами премії пам'яті Альфреда Нобеля з економіки "за пріоритетний вклад в аналіз некооперативних ігор".
Сутність теорії ігор полягає у встановленні оптимальної (у тому чи іншому змісті) стратегії поведінки в конфліктних ситуаціях. Метою теорії ігор є визначення оптимальної стратегії для кожного гравця.
Стратегією гравця називається сукупність правил, що обумовлюють вибір його дій при кожному особистому ході залежно від наявної ситуації.
Під конфліктом розуміється ситуація, в якій стикаються інтереси двох чи більше сторін, які переслідують різні (інколи протилежні) цілі. Кожна з сторін-учасників конфліктних ситуацій може у певний спосіб впливати на хід подій, але не має змоги повністю ним керувати. Конфліктні ситуації виникають під час вирішення різноманітних економічних проблем (відносини між організаціями-виробниками і споживачами, торгівля, економічна конкуренція тощо).
Щоб дослідити конфліктну ситуацію будують її формалізовану спрощену модель, яка називається грою. Теорія ігор встановлює для різних класів конфліктних ситуацій оптимальні лінії поведінки учасників – стратегії гравців, що забезпечують рівновагу у грі. Оптимальні стратегії гравців гарантують кожному з них якийсь виграш, причому такий, що відхід будь-якого з учасників від узгодженої стратегії може тільки зменшити його виграш.
Ігри різняться за числом учасників, характеристиками так званих платіжних функцій, які визначають виграш кожного гравця залежно від його поведінки і поведінки інших учасників конфлікту, за інформацією про ситуацію, що склалася та яка є в розпорядженні партнерів, за правилами, що обмежують вибір лінії поведінки учасників, за можливостями укладання угод між ними і входження в коаліції, за визначенням поняття "рівноваги" чи "справедливого вирішення гри".
Наприклад, теорія ігор математично описує характерні для ринкової економіки явища конкуренції у вигляді гри. Простий варіант передбачає протистояння двох конкурентів за ринок збуту. Складні варіанти передбачають, що в грі беруть участь багато супротивників, вступаючи при цьому між собою в постійні або в тимчасові союзи. У першому випадку гра називається парною, в другому – гра л-осіб, або множинна. У виразі наявності союзів гра має назву коаліційної.
Складовою теорії ігор виступає статистична теорія ігор. Це розділ сучасної прикладної математики, який вивчає методи обґрунтування оптимальних рішень в конфліктних ситуаціях.
У теорії статистичних ігор наявні такі поняття як вихідна стратегічна гра і власне статистична гра. В цій теорії першого гравця називають природою, вкладаючи в це поняття сукупність обставин, в яких доводиться приймати рішення другому гравцю, якого називають статистиком.
Якщо виграш одного гравця дорівнює програшу іншого, то гра називається антагоністичною або грою з нульовою сумою. У процесі гри її учасники здійснюють ходи. Ходом гравця називається вибір та здійснення однієї із передбачених правилами дій.
Ходи бувають двох видів: особисті та випадкові. Особистий хід – це свідомий вибір гравцем одного з можливих варіантів дій. У подальшому ми будемо розглядати тільки особисті ходи гравців. Випадковий хід – це випадково вибрана дія.
Для того, щоб вирішити гру, або знайти рішення гри необхідно для кожного гравця вибрати стратегію, яка б відповідала умові оптимальності. Це означає, що один із гравців повинен одержати максимальний виграш, у той час як другий дотримується своєї стратегії. Такі стратегії називаються оптимальними.
Оптимальні стратегії мають також відповідати умові стійкості, тобто будь-кому з гравців повинно бути невигідно відмовитися від своєї стратегії у цій грі.
Якщо гра повторюється багато разів, то тоді гравців може цікавити не виграш і програш кожного разу в кожній конкретній партії, а середній виграш (програш) в усіх партіях.
Статистична теорія ігор відрізняється від стратегічної теорії ігор. Так, стратегічна теорія ігор передбачає такі умови:
– активні дії обох гравців;
– обидва гравці поводяться розумно з погляду своїх інтересів;
– повна невизначеність у виборі стратегії кожним гравцем;
– обидва гравці діють на підставі детермінованої інформації, визначеної матрицею втрат.
На відміну від стратегічної статистична теорія ігор відбувається за таких умові
– природа не є активним гравцем, тобто вона "нерозумна" і не протидіє максимальному виграшу другого гравця;
– статистик (другий гравець) намагається виграти гру в уявного противника, тобто у природи;
– часткова невизначеність у виборі стратегії;
– природа розвивається і діє відповідно до об'єктивно існуючих законів;
– наявність можливості у статистика поступового вивчення законів, зокрема, на основі статистичного експерименту.
Застосування теорії статистичних ігор розглянемо на конкретному прикладі.
Приклад. Швейна фабрика випускає жіночі плащі та пальта, реалізація яких здійснюється через фірмовий магазин і залежить від природних кліматичних умов, насамперед від погодних. Основні виробничі показники фабрики наведені в табл. 13.3 з додатково введеними їх буквеними позначеннями.
Визначити оптимальну стратегію реалізації продукції швейної фабрики, яка б сприяла отриманню максимального прибутку.
Розв'язання
1. Визначимо спочатку гравців. У ролі природи (перший гравець) тут виступатиме попит на продукцію. Множину станів природи (стратегії) позначимо
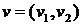 ,
,
де 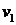 – попит на продукцію фабрики в теплу погоду;
– попит на продукцію фабрики в теплу погоду;
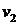 – попит на продукцію в прохолодну погоду.
– попит на продукцію в прохолодну погоду.
У ролі статистика виступатиме фабрика (другий гравець), яка має два можливі варіанти (стратегії) розвитку подій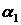 ,
, 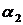 які означають, що обсяги реалізації продукції залежать від погодних умов – відповідно теплої і прохолодної погоди.
які означають, що обсяги реалізації продукції залежать від погодних умов – відповідно теплої і прохолодної погоди.
Передбачається, що статистик, який займає активну позицію, може оцінювати наслідки кожного варіанта реалізації продукції залежно від стану природи.
Таблиця 13.3. Основні виробничі показники швейної фабрики за видами продукції за березень – квітень
Вид продукції | Собівартість одиниці, грн (г) | Ціна, грн (р) | Обсяг реалізації, од. (q) | |
Тепла погода | Прохолодна погода | |||
Плащі | 400 | 800 | 2000 | 1080 |
Демісезонні пальта | 1350 | 2430 | 700 | 1100 |
2. Функція 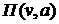 буде функцією прибутку. її можна задати аналітичним виразом
буде функцією прибутку. її можна задати аналітичним виразом
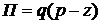 .
.
3. Розглянемо стратегії гравців, зробивши відповідні розрахунки очікуваного прибутку:
– в умовах здійснення стратегії природи ujy що відповідає попиту на продукцію фабрики в теплу погоду, очікуваний прибуток становитиме:
П = 2000(800 - 400) + 700(2430 - 1350) = 1556 (тис. грн);
– взявши за основу стратегію природи v2, що передбачає попит на продукцію в прохолодну погоду, фабрика отримає прибуток:
П = 1080(800 - 400) + 1100(2430 - 1350) = 1620 (тис. грн);
– якщо фабрика прийме стратегію а1, яка відповідає теплій погоді, тоді їй вдасться продати всі плащі, але тільки частину пальт (700 із 1100 од.) та отримати прибуток:
П= 2000(800 - 400) + 700(2430 - 1350) - (110 - 700)х
х (2430 - 1350) = 1124 (тис. грн);
– коли фабрика обере стратегію а2, яка відповідає прохолодній погоді, то вона продасть усі пальта і частину плащів (1080 із 2000 од.) і отримає прибуток:
П = 1080(800 - 400) + 1100(2430 - 1350) - (2000 - 1080) х
х (800 - 400) = 1252 (тис. грн).
4. На основі одержаних даних побудуємо платіжну матрицю (матрицю гри) – табл. 13.4.
Таблиця 13.4. Матриця прибутку 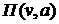 фабрики, тис. грн
фабрики, тис. грн
a v |
|
| min за рядками |
| 1556 | 1124 | 1124 |
| 1252 | 1620 | 1252 |
max за стовпцями | 1556 | 1620 | — |
Із платіжної матриці видно, що перший гравець "природа" ні за яких варіантів розвитку подій не отримає прибуток менший ніж 1124 тис. грн. Проте за збігу погодних умов з обраною стратегією, виграш фабрики становитиме 1556 або 1620 тис. грн. Якщо другий гравець "фабрика" буде постійно застосовувати стратегію 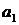 , а гравець природа – стратегію
, а гравець природа – стратегію 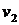 , то виграш зменшиться до 1252 тис. грн.
, то виграш зменшиться до 1252 тис. грн.
Подібна тенденція відбуватиметься, коли гравець "фабрика" буде постійно застосовувати стратегію 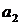 , а гравець "природа" – стратегію
, а гравець "природа" – стратегію 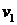 .
.
Отже, можна зробити висновок, що найбільший прибуток фабрика може одержати, якщо буде почергово застосовувати стратегії at та а2. Така стратегія називається змішаною, а її складові (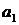 та
та 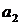 ) – чистими стратегіями.
) – чистими стратегіями.
Оптимізація змішаної стратегії дасть змогу другому гравцю (статистика) – фабриці завжди отримувати середнє значення виграшу незалежно від стратегії першого гравця (природа).
Покажемо це на нашому прикладі. Для цього позначимо частоту застосування фабрикою стратегії 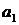 через
через 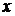 . Виходячи з цього, частота застосування ним стратегії
. Виходячи з цього, частота застосування ним стратегії 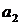 становитиме
становитиме 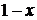 .
.
Якщо фабрика застосує оптимальну змішану стратегію, то і за стратегії 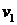 (тепла погода) і за стратегії
(тепла погода) і за стратегії 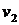 (прохолодна погода) другого гравця (природа) вона повинна отримати однаковий середній прибуток:
(прохолодна погода) другого гравця (природа) вона повинна отримати однаковий середній прибуток:
1556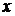 + 1124(1 -
+ 1124(1 - 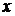 ) = 1252
) = 1252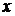 + 1620(1 -
+ 1620(1 - 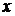 );
);
1556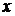 + 1124 - 1124
+ 1124 - 1124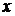 - 1252
- 1252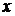 + 1620 - 1620
+ 1620 - 1620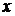 ;
;
800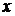 = 496;
= 496;
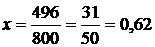 ;
;
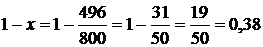 .
.
Справді, при застосуванні стратегії 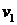 (тепла погода) гравця природи середній прибуток фабрики дорівнюватиме
(тепла погода) гравця природи середній прибуток фабрики дорівнюватиме
1556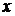 + 1124(1 -
+ 1124(1 - 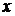 ) = 1556 ž 0,62 +1124 ž 0,38 =
) = 1556 ž 0,62 +1124 ž 0,38 =
= 1391,84 (тис. грн).
При реалізації стратегії v2 (прохолодна погода) гравця природи середній прибуток фабрики становитиме:
1252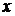 + 1620(1 -
+ 1620(1 - 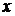 ) = 1252 ž 0,62 + 1620 ž 0,38 =
) = 1252 ž 0,62 + 1620 ž 0,38 =
= 1391,84 (тис. грн).
Таким чином, гравець фабрика, застосовуючи чисті стратегії 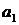 та
та 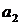 у відношенні 31 до 19 (приблизно 3 до 2), матиме оптимальну змішану стратегію, що забезпечить йому у будь-якому випадку середній прибуток розміром 1391,84 тис. грн, тобто середній платіж дорівнюватиме 1391,84 тис. грн. Такий середній платіж, який одержують при реалізації оптимальної стратегії, називається ціною гри.
у відношенні 31 до 19 (приблизно 3 до 2), матиме оптимальну змішану стратегію, що забезпечить йому у будь-якому випадку середній прибуток розміром 1391,84 тис. грн, тобто середній платіж дорівнюватиме 1391,84 тис. грн. Такий середній платіж, який одержують при реалізації оптимальної стратегії, називається ціною гри.
Визначимо також кількість пальт і плащів, які фабрика повинна випускати для одержання максимального прибутку:
(2000 плащів + 700 пальт) ž 0,62 + (1080 плащів +
+ 1100 пальт) ž 0,38 = 1240 плащів + 434 пальта +
+ 410,4 плащів + 418 пальт = 1650 плащів + 852 пальта.
Таким чином, оптимальна стратегія фабрики означає 1650 плащів та 852 пальта. За таких умова вона отримає середній прибуток розміром 1391,84 тис. грн.
Ігрові підходи використовуються економістами як на макрорівні при розробці моделей, в яких враховуються інтереси різних ланок економіки, так і на рівні підприємства для вибору оптимальних рішень при створенні запасів сировини, матеріалів, напівфабрикатів, підвищенні якості продукції, маркетинговій діяльності тощо.
Перевагою теорії ігор є можливість розширення поняття оптимальності, включаючи, наприклад, компромісне рішення, яке йде на задоволення різних потреб у грі. З іншого боку, в економічних задачах, аналіз яких зводиться до математичного програмування або до теорії ігор, при елементарній оцінці ефективності варіанта, кількість варіантів настільки велика, що вибрати оптимальний, як правило, вкрай важко.
Значним обмеженням теорії ігор є єдиний показник виграшу як характеристика ефективності, хоча на практиці при вирішенні більшості економічних завдань зустрічаються декілька показників ефективності. Крім того, в економіці здебільшого виникають такі ситуації, коли інтереси партнерів не носять антагоністичного характеру. Це свідчить про необхідність подальшого розвитку апарату теорії ігор відповідно до економічних реалій і виробничої необхідності.
НАВЧАЛЬНИЙ ТРЕНІНГ
Розділ 14. ЕВРИСТИЧНІ МЕТОДИ ТА ЇХ ЗАСТОСУВАННЯ В ЕКОНОМІЧНОМУ АНАЛІЗІ
14.1. Сутність і групування евристичних методів
14.2. Метод мозкового штурму
14.3. Методи експертних оцінок
14.4. Методи асоціацій та аналогій
14.5. Інші евристичні методи
НАВЧАЛЬНИЙ ТРЕНІНГ
Розділ 15. АНАЛІЗ РЕЗЕРВІВ ПІДВИЩЕННЯ ЕФЕКТИВНОСТІ ГОСПОДАРСЬКОЇ ДІЯЛЬНОСТІ