Логіка - Мозгова Н.Г. - 7. Об'єднана класифікація простих категоричних суджень за якістю та кількістю

Оскільки кожне судження одночасно має якісну і кількісну характеристику, то буде доцільним об'єднати два попередніх поділи суджень за якістю і кількістю. У результаті цього об'єднання отримаємо такі чотири типи простих суджень: загальностверджувальне А (SР) (від латинського - стверджувати), частковостверджувальне І (SР), загальнозаперечне Е (SР) (від латинського слова - заперечувати), частковозаперечне О (SР). Одиничні за кількістю судження відносять відповідно до загальностверджувальних або загальнозаперечних, оскільки в них мова йде не про частину предметів даного класу, а про один предмет, який становить весь даний клас предметів.

А(SР) - загальностверджувальне, тобто загальне за кількістю та стверджувальне за якістю, судження. Наприклад, "Будь-який злочин є карним вчинком". Його логічна формула: "Всі S є Р". Кванторне слово "всі" характеризує кількість, а стверджувальна логічна зв'язка "є" - якість судження.

I(SР) - частковостверджувальне, тобто часткове за кількістю та стверджувальне за якістю судження. Наприклад, "Деякі студенти є відмінниками навчання". Його логічна формула: "Деякі S є Р". На кількість судження вказує кванторне слово "деякі", а на якість - стверджувальна логічна зв'язка "є".

Е(SР) -загальнозаперечне, тобто загальне за кількістю та заперечне за якістю судження. Наприклад, "Жоден студент не є професором". Його логічна формула: "Жодне S не є Р". Кількість судження виражається кванторним словом "жодне", а якість - заперечною логічною зв'язкою "не є".

O(SР) - частковозаперечне, тобто часткове за кількістю та заперечне за якістю судження. Наприклад, "Деякі люди не є студентами". Його логічна формула: "Деякі S не є Р". На кількість судження вказує кванторне слово "деякі", а на якість-логічна зв'язка "не є".

Логічні формули простого категоричного судження: "Всі S є Р", "Деякі S є Р", "Жодне S не є Р", "Деякі S не є Р" будемо називати нормальними формами судження.

Для того, щоб установити тип (А, Е, І, О) будь-якого простого судження необхідно:

1. Вияснити його смисл: стверджувальне воно чи заперечне; що саме стверджується (заперечується), тобто що є S і Р судження; про яку частину предметів 8 йде мова у судженні.

2. Подати його у нормальній формі, S і Р при цьому повинні зберігати свої місця відповідно до логічного наголосу першопочаткової форми висловлювання. Наприклад, "Бувають хиби, схожі на істину". 1) інтуїтивно ясно, що це судження стверджувальне; в ньому S - "хиби", а Р - "істини"; слово "бувають" вказує на те, що мова йде про частину "хиб" (S ). Отже, 2) в нормальній формі воно буде мати вигляд: "Деякі хиби є схожими на істину" ("Деякі S є Р") - це судження І(SР) - частковостверджувальне. Другий приклад: "не все однаково придатне для всіх". 1) інтуїтивно ясно, що це судження щось заперечує; "однаково придатне" — означає "не придатне" або "не є придатним"; "не все" - означає частину, тобто "дещо" (речі, професія, стиль життя тощо); S -"дещо", а Р - "придатне для всіх людей". Отже, 2) в нормальній формі воно буде таким "Дещо не є придатним для всіх людей" - це судження O(SР) - частковозаперечне.

8. Розподіленість термінів у категоричних судженнях

Термін (S,Р) вважається розподіленим, якщо його обсяг повністю включається або виключається з обсягу іншого терміна. Розподілений термін позначається - S+, Р+.

Термін (S,Р) вважається нерозподіленим, якщо його обсяг частково включається або виключається з обсягу іншого терміна. Нерозподілений термін позначається - S-, Р-.

Залежно від чотирьох типів простих категоричних суджень існують такі випадки розподіленості термінів.

Судження А(SP).

Його формула: "Всі S є Р". Існує два випадки розподіленості S та Р.

1-й випадок. Наприклад, "Всі студенти-філологи є студентами". Відношення між 8 (студенти-філологи) та Р (студенти) подамо у вигляді кіл Ейлера:

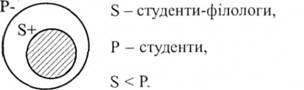
Оскільки "всі студенти - філологи" включаються в обсяг предиката, то S + буде розподіленим. У судженні логічний наголос стоїть на S , тобто з обсягу "студентів" (Р) виключається та частина обсягу, яка належить до S . Р-, таким чином, буде нерозподіленим.

2-й випадок. Наприклад, "Всі квадрати - прямокутні ромби".

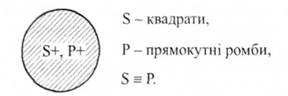
Це виділяюче судження, значить у ньому обсяги 8 і Р повністю збігаються або включають одне одне, тоді і Б, і Р будуть розподіленими.

Судження І(SР).

Його формула "Деякі S є Р". Існує два найбільш розповсюджених випадки розподіленості S та Р.

1-й випадок. Наприклад, "Деякі студенти є відмінниками навчання".

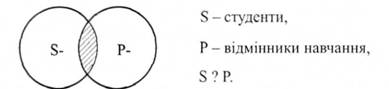
Відношення між обсягами S та Р є невизначеним. Оскільки S та Р частково включають обсяги один одного, то і S , і Р будуть нерозподіленими. 2-й випадок. Наприклад, "Деякі юристи є адвокатами".

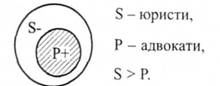
Оскільки всі адвокати (Р) включаються в обсяг S , то Р + - буде розподіленим. Логічний наголос судження стоїть на Р, тобто з обсягу юристів (S ), виключається та частина обсягу, яка належить до Р, тоді Б буде нерозподіленим.

Судження Е(SP).

Його формула "Жодне S не є Р". Тут можливий лише один випадок розподіленості S та Р. Наприклад, "Жодна кішка не є собакою".

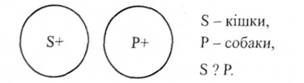
Оскільки і S, і Р повністю виключаються з обсягів один одного, то обоє вони будуть розподіленими.

Судження O(SР).

Його формула "Деякі 8 не є Р". Тут найбільш розповсюдженими є два випадки розподіленості термінів.

1-й випадок. Наприклад, "Деякі юристи не є адвокатами".

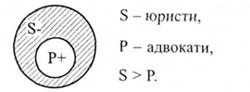
Оскільки мова йде про "деяких юристів", тобто про частину S, то суб'єкт буде нерозподіленим. Предикат же повністю включається в обсяг суб'єкта, отже він буде розподіленим.

2-й випадок. Наприклад, "Деякі студенти не є відмінниками навчання".

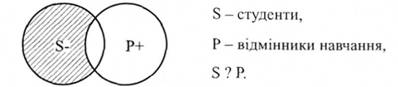
Оскільки S (студенти) частково (деякі S) включається в обсяг Р (тільки частиною студентів відмінників), то S буде нерозподіленим. Р - відмінники навчання — береться в повному обсязі (повністю виключається з обсягу S).

Отже, S завжди розподілений у загальних судженнях і нерозподілений у часткових; Р завжди розподілений у заперечних судженнях, а в стверджувальних він буде розподіленим за умови, що Р<S.

Для того, щоб визначити розподіленість термінів у даному судженні необхідно:

1. Привести його до нормальної форми.

2. Сформулювати обернене судження, тобто поставити Р на перше місце, а S на друге.

3. Виходячи з виявленого співвідношення обсягів S та Р, зобразити його колами Ейлера.

4. Проставити розподіленість термінів. Наприклад, "Електрон має негативний заряд".

1. Нормальна форма: "Всі електрони є негативно зарядженими частками" - А(S Р).

2. Але А(S Р) має два випадки співвідношення обсягів S і Р (S < Р, S = Р) при одній і тій же логічній формулі: "Всі S є Р". У першому випадку (S < Р), обернене буде: "Деякі Р є S ", а в другому (S = Р) - "Всі Р є S ". У нашому випадку правильним оберненим судженням буде: "Всі негативно заряджені частки є електронами". Отже:

Твердження про те, що "Деякі негативно заряджені частки є електронами" було б хибним, бо крім електрона таких часток не існує.

Література для поглибленого вивчення розділу

A. Основна.

1. Гетманова А.Д. Логика. - М.: Новая школа, 1995. - С. 60-69.

2. Жеребкін В.Є. Логіка. - X.: Основа; К.: Знання, 1999. - С. 62-85.

3. Кириллов В.И., Старченко A.A. Логика. - М.: Высшая школа, 1995. -С. 63-106.

4. Конвсрський А.Є. Логіка. - К.: Четверта хвиля, 1998 - С. 170-192.

5. Иванов Е.А. Логика. - М.: Издательство БЕК, 1996. - С. 104-137.

6. Свинцов В.И. Логика. - М.: Скорина; Весь мир, 1998. - С. 80-101.

B. Додаткова.

1. Ивин A.A. Искусство правильно мыслить. - М.: Просвещение, 1990. -С. 154-209.

2. Карнап Р. Значение и необходимость. - М.: Наука, 1968. - С. 97-102.

3. Кондаков Н.И. Логический словарь-справочник. - М.: Наука, 1975. Статті: высказывание, единичное суждение, категорическое суждение, логический квадрат, необходимости суждения, общеотрицательное суждение, общеутвердительное суждение, отношение между суждениями, простое суждение, сложное суждение, частноотрицательное суждение, частноутвердителыюе суждение та інші статті до даної теми.

4. Логические методы и формы научного познания. - К.: Наукова думка, 1984.-200 с.

5. Мельников В.Н. Логические задачи. - К.; Одесса: Вища школа, 1989. -С. 117-126.

6. Свинцов В.И. Смысловой анализ и обработка текста. - М: Наука, 1979.-272 с.