Логіка - Мозгова Н.Г. - 4. Відношення часткової сумісності

*Закон тотожності як закон правильного мислення є певною формою відображення закону об'єктивної дійсності - визначеності, певної відносної сталості властивостей предметів і явищ. Але його вимоги стосуються тільки думок: він вимагає однозначності думки про деяку властивість предмета в даному міркуванні. Закони логіки мають силу в мисленні тоді, коли ми застосовуємо їх, враховуючи такі умови: а) мова повинна йти про один і той самий предмет думки; S) мова повинна йти тільки про одне відношення (властивість) предмета думки; с) думка про предмет міркування повинна бути обмежена певним часом. Усі три умови визначають правильність застосованих усіх основних законів логіки.

*Закон тотожності формулюється так: Кожна думка про окремий предмет чи його властивість у межах даного міркування повинна зберігати один і той самий зміст. Закон тотожності записується формулою "А = А" (А тотожно А).

Отже, закон тотожності відображає однозначність думок у процесі мислення. Логічною формою вираження ототожнення є ствердження (судження). Ототожнення думки самої з собою в процесі мислення пов'язане зі збереженням її обсягу та змісту.

Найпоширенішим видом помилки, яка виникає внаслідок порушення закону тотожності, є підміна понять. Підміна понять грунтується на явищі багатозначності слів. Прикладом підміни понять є такий діалог. "Розізлившись на кума, Микола сказав:

- Ти, Петре, ніколи не будеш людиною, бо ти - свиня.

- Ну, це ти вже забрехався куме, - відповів Петро.

- Аніскільки я не забрехався, і можу це довести, - злорадно сказав Микола.

- Доведи, - став вимагати Петро.

- Підожди, доведу, - з тією ж злорадністю у голосі відповів Микола. Обоє замовкли. Петро лякливо чекав, і його розбирала злість на

Миколу. Раптом Микола спитав:

- А що, Петре, є у тебе п'ятачок?

- Є, але тобі я не дам, - злісно відповів Петро.

- Як, у тебе є п'ятачок, і ти після цього скажеш, що ти не свиня! - скрикнув радісно Микола".

4. Відношення часткової сумісності

Усі логічні відношення між простими судженнями, крім еквівалентності, можна наочно зобразити за допомогою логічного квадрата.

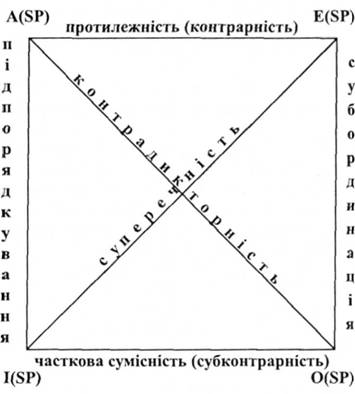
Його вершини символізують прості категоричні судження - А, Е, І, О; сторони та діагоналі — логічні відношення між судженнями. Верхня сторона символізує відношення (А - Е) протилежності (контрарності); нижня сторона - відношення (І - О) часткової сумісності (субконтрарності); дві вертикальні сторони - відношення (А -1, Е - О) підпорядкування (субординації); діагоналі - відношення (А - О, Е -I) суперечності (контрадикторності).

Частково сумісними є судження I(SР) — O(SР), які не можуть бути одночасно хибними.

З таблиці видно, що ці судження можуть бути одночасно істинними, або мати протилежні значення істинності. Наприклад, "Деякі студенти є відмінниками" - судження І(8Р), істинне; "Деякі студенти не є відмінниками" - судження О(SР), істинне. "Деякі студенти є академіками" - судження І(SР), хибне; "Деякі студенти не є академіками" - судження O(SР), істинне. Неможливим є випадок, коли б ці судження були одночасно хибними, тому їх називають хиба-несумісними (х - несумісні).

5. Відношення підпорядкування

У відношенні підпорядкування знаходяться такі пари суджень: А(SР) – I(SР), Е(SР) - O(SР). Загальні судження (А, Е) називають підпорядковуючими, а часткові (І, О) - підпорядкованими. Відношення підпорядкування існує у всіх можливих випадках значень їх істинності, крім одного — коли загальне є істинним, а часткове -хибним. У таблиці це можна подати так:

З таблиці видно, що:

1) 3 істинного загального судження (А, Е) завжди випливає істинне часткове (підпорядковане -1,0). Наприклад, "Жоден прокурор не є адвокатом" - "Деякі прокурори не є адвокатами".

2) Якщо загальне є хибним, то часткове може бути й істинним, і хибним. Наприклад, "Усі люди - юристи" (А, хибне) - "Деякі люди -юристи" (І, істинне); "Усі люди - безсмертні" (А, хиба) - "Деякі люди - безсмертні" (І, хиба).

3) Якщо підпорядковане (1, О) - істинне, то підпорядковуюче (А, Е) може бути і істинним, і хибним. Наприклад, "Деякі люди - злочинці" (І, істинне) - "Усі люди - злочинці" (А, хибне); "Деякі студенти-юристи вивчають логіку" (І, істинне) - "Усі студенти-юристи вивчають логіку" (А, істинне).

4) 3 хибного часткового судження завжди випливає хибне загальне. Наприклад, "Деякі судді не є юристами" - "Жоден суддя не є юристом".

5) Неможливим є випадок, коли б загальне судження (А, Е) було істинним, а часткове (І, О) - хибним.