Менеджмент организаций - Киржнер Л.А. - Мера риска

Можно ли измерить риск? Теория риска и многолетний опыт зарубежных фирм, учитывающих фактор риска, отвечает на этот вопрос утвердительно. Одним из основных методов, позволяющих найти меру риска, является теория вероятностей. Объектом теории вероятностей является измерение степени возможности случайных различных результатов.

Случайное событие в математической статистике определяется как событие, которое может произойти или не произойти, в отличие от достоверного события, которое обязательно осуществляется (при данных условиях) и невозможного события, осуществление которого при данных условиях исключается, случайное событие в математической статистике определяется, как событие, которое может произойти или не произойти. Случайные события становятся предметом теории вероятностей только тогда, когда с ним связываются определенные числовые характеристики — их вероятности.

Различают математическую и статистическую вероятность события. Измерение вероятностей основывается на подсчете шансов. Математическая вероятность того, что событие А произойдет, измеряется отношением числа шансов (равновозможных и несовместимых), благоприятствующих данному событию А (М), к общему числу благоприятствующих и не благоприятствующих шансов (N):

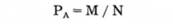
Такое определение вероятности называется классическим.

Кроме математической вероятности случайного события имеется статистическое понимание вероятности. Если в результате достаточно большого числа испытаний установлено, что частота случайного события М(m/n) приближается к некоторой величине, то эту величину в силу закона больших чисел, принимают за численное значение вероятности данного события (РА). Ясно, что установление вероятности случайного события опытным путем носит несколько неопределенный характер.

Бели вероятность случайного события определяется до испытания, приведшего к определенному исходу, то численное значение этой вероятности называют априорным (до опытным).

Вероятность события после опыта, приведшего к определенному результату, в отличие от опытной вероятности называют апостериорной вероятностью.

Вероятность того, что событие А не произойдет (qa), исчисляется в соответствии с определением вероятности как отношение числа шансов, не благоприятствующих событию А, к общему числу шансов. Если N — общее число шансов и событию А благоприятствует М шансов, то не благоприятствует ему N-М шансов. Тогда: -

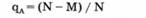
Полученную вероятность называют вероятностью противоположного события.

Сумма вероятностей двух противоположных событий, т.е. таких, из которых в результате испытания может произойти либо одно, либо другое, равна единице:

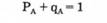
Отсюда вытекает, что зная вероятность события А можно вычитанием ее из единицы определить вероятность того, что А не произойдет:

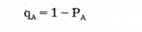
Если N случаев благоприятствует событию А(М= N), то вероятность события А равна единице. Такое событие называется достоверным.

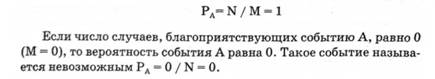
Чем ближе вероятность событий к единице, тем оно достовернее. Чем ближе вероятность события к нулю, тем оно мало вероятнее.

Если речь идет об единичном испытании, то при вероятности Р < 0,01 действует "принцип практической невозможности маловероятных событий", состоящей в том, что, если какое-нибудь событие имеет малую вероятность, то при единичном испытании можно практически считать, что это событие не произойдет. Из этого принципа вытекает важное следствие для событий, вероятности которых близки к единице (Р > 0,99), то практически при единственном испытании можно считать, что это событие произойдет наверняка.

Случайные события в процессе их наблюдения повторяются с определенной частотой. Частота случайного события, как уже отмечалось, представляет собой отношение числа проявлений этого события к общему числу наблюдений. Частота обычно обладает статистической устойчивостью в том смысле, что при многократном наблюдении ее значения мало меняются. Таким образом, частоты случайного события как бы группируются около некоторого числа. Устойчивость частоты отражает некоторое объективное свойство случайного события, заключающееся в определенной степени его возможности.

Но необходимо помнить, что частота — это результат того, что уже произошло, вероятность предсказания того, что должно случиться в будущем. Чем больше опытом проведено при определении частоты, тем точнее, объективнее получается вероятность. Это проявление одно из важнейших законов, управляющих случаем — так называемого "Закона больших чисел". Это классический способ определения вероятностей и его формула и сегодня находит широкое применение при расчетах риска неудачи.

Математический аппарат теории вероятностей позволяет производить действия с вероятностями (сложение, умножение, деление), определять полную вероятность события А, а строить полигон распределения, определять наивероятнейшую частоту, рассчитывать вероятность конкретной частоты по формуле общего члена разложения бинома Ньютона. Для различных ситуаций могут быть использованы локальная и интегральная формулы Лапласа.

Таким образом, вероятность позволяет прогнозировать случайные события. Она дает им количественную и качественную характеристику. При этом уровень неопределенности и степень риска уменьшаются.

Вероятность означает также и возможность получения определенного результата. Применительно к экономическим задачам, связанным с риском методы теории вероятностей сводятся к определению значений вероятности наступления событий и к выбору из возможных событий самого предпочтительного события исходя из наибольшей величины математического ожидания.

Математическое ожидание случайной дискретной величины равно сумме произведений каждого возможного значения этой величины на его вероятность:

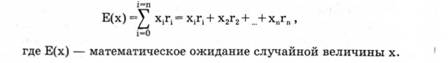
Математическое ожидание случайной величины равно среднему ее значению, взвешенному по вероятностям: Е(х) = х. Такая средняя называется стохастической"

Следует различать объективную и субъективную вероятность. Объективная вероятность — это вероятность, базирующаяся на расчете частоты, с которой происходит данный процесс или явление. Субъективная вероятность — это вероятность, основанная на предположении о возможности получения данного результата. Она основана на использовании субъективных критериев, которые базируются на различных предложениях. К ним относятся: суждение оценивающего, его личный опыт, оценка эксперта, мнение финансового консультанта и т.п. Когда вероятность определяется субъективно, то разные люди могут устанавливать разное значение дел одного и того же события и делать каждый свой выбор.

Важное место при этом занимает прием экспертной оценки, т.е. проведение экспертизы и использование его результатов при обосновании значения вероятности. Прием экспертной оценки представляет собой комплекс логических и математико-статистических методов и процедур, связанных с деятельностью эксперта по переработке необходимой для анализа и принятия решений информации. Прием экспертной оценки основан на использовании способности специалиста, находить нужное, наиболее эффективное решение.

Вероятность позволяет прогнозировать случайные события. Она дает им количественную и качественную характеристику. При этом уровень неопределенности и степень риска уменьшается. Неопределенность хозяйственной ситуации во многом определяется, как уже отмечалось, и фактором противодействия: катастрофа, пожар идр. природные явления; война, революция, забастовка, конфликты в трудовых коллективах, конкуренция, нарушения договорных обязательств, изменение спроса.

Предприниматель, менеджер в процессе своих действий должен выбрать такую стратегию, которая позволит ему уменьшить степень противодействия, что в свою очередь позволит снизить и степень риска.

Математический аппарат для выбора стратегии в конкретных ситуациях дает теория игр. Она позволяет предпринимателю, менеджеру лучше понимать конкурентную обстановку, свести к минимуму степень риска. Анализ с помощью приемов теории игр побуждает предпринимателя, менеджера рассматривать все возможные альтернативы, как своих действий, так и стратегии партнеров, конкурентов. Формализация данного процесса позволяет уменьшить понимание, принимающего решение проблемы в целом.

Таким образом, мы можем сделать вывод, что риск имеет математически выраженную вероятность наступления события, которая опирается на статистические данные и может быть рассчитана с достаточно высокой степенью точности.

Для несложных задач нам важно знать сколько раз проверять, чтобы риск оказался минимальным, т.е. как определить необходимое число проверок?

Предположим, фирма закупила комплект оборудования. Она задалась целью выполнить столько проверок, сколько нужно для обеспечения необходимого ей минимального риска. Как определить необходимое число проверок?

Если обозначить вероятность удачной проверки работы комплекта оборудования Р, то 1—Р станет обозначать вероятность неудачи при одной проверке. При двух проверках вероятность того, что оба раза нас постигнет неудача - мы не найдем неисправность, естественно, меньше. По теории вероятности она будет равна:

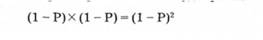
Действительно, вычтя из вероятности всех возможных исходов (она, как мы знаем равна 1) вероятность того, что все n раз нас постигла неудача, мы исключаем те случаи, которые нас не устраивают. В итоге, поэтому и остается вероятность получения неудачи хотя бы один раз (или не менее одного раза).

Из предыдущей формулы путем несложных преобразований уже нетрудно найти само n — конкретное число проверок, из которых хотя бы одна должна привести к удаче. Группируя члены и логарифмируя, получим:

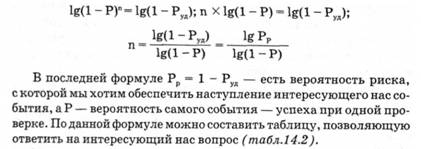
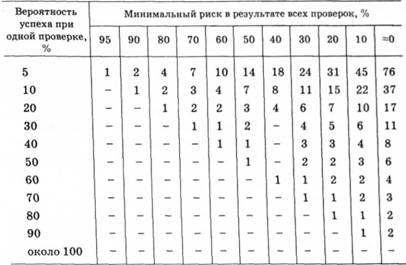
На основании таблицы, например, с вероятностью успеха при одной проверке 50 % и задаваясь требуемой вероятностью получения минимального риска всех проверок, скажем 20%, получим требуемое число проверок, равное 2. Это значит, что из двух проверок хотя бы одна окажется удачной — неисправность в оборудовании будет выявлена. Хотите уменьшить риск до 10% — увеличьте число проверок до трех.

Мы рассматривали задачи, которые решаются на основе теории вероятностей, речь в которых идет о случайных событиях, т.е. таких, которые по воле случая могли как произойти, так и не произойти. Но в реальной жизни возникают более сложные ситуации и получение односложного ответа "да" или "нет" нас часто не устраивает. Поэтому мы можем использовать более сложные правила современной теории вероятностей, которые будут рассмотрены ниже.

Табл.14.2. Сколько нужно сделать проверок, чтобы хотя бы одна из них привела к успеху?