Менеджмент підприємства - Хомяков В.І. - РОЗВ'ЯЗАННЯ ГРАФІКА "ВИТРАТИ-РЕЗУЛЬТАТИ" ТА КРИВОЇ ПОПИТУ

На довгостроковому етапі фірма може змінити всі використані фактори виробництва.

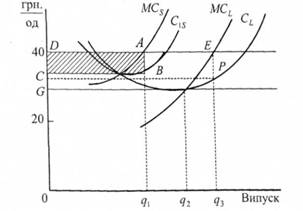
Рисунок 5.17. Оптимізація обсягу виробництва фірми на довгостроковому етапі

Рисунок 5.17 показує, як конкурентна фірма приймає довгострокове рішення відносно об'єкта виробництва, що забезпечує максимум прибутку. Як і в попередньому прикладі, фірма приймає постійну ринкову ціну (що дорівнює, наприклад, 40 грн.). Короткострокова крива середніх валових витрат, що припадають на одиницю продукції C1s, і короткострокова крива граничних витрат MCs розміщені так, що фірма має позитивний прибуток, зображений прямокутником АВСД за обсягу виробництва q1, при цьому MCs = МР = Ц, де МР - граничний дохід.

Довгострокова крива витрат на одиницю продукції CiL відображає позитивний ефект масштабу виробництва для всіх обсягів випуску продукції до q2 і негативний за більших обсягів виробництва. Довгострокова крива граничних витрат MCL перетинає довгострокову криву витрат C1L в точці q2 - точці довгострокових мінімальних витрат.

Якщо фірма вважає, що ринкова ціна залишається незмінною (40 грн.), вона вирішує збільшити виробництво продукції до величини qз, за якої довгострокові граничні витрати дорівнюють 40 грн. Коли таке розширення виробництва завершене, граничний прибуток фірми зростає з АВ до EF, а її валовий прибуток збільшується з ABCD до EFGD. Обсяг виробництва q3 максимізує прибуток фірми, тому що за будь-якого більш низького обсягу виробництва, скажімо q2, граничний дохід від додаткового виробництва вищий від граничних витрат і бажане подальше розширення. Але за будь-якого обсягу виробництва, вищого від q3, граничні витрати вищі за граничний дохід, і тому додаткове виробництво веде до скорочення прибутку. В результаті, на довгостроковому етапі конкурентна фірма максимізує свій прибуток за такого обсягу виробництва, за якого довгострокові граничні витрати дорівнюють ціні.

Таким чином, ціна в 40 грн. стимулює фірму збільшувати обсяг виробництва і забезпечує їй позитивний прибуток. А це означає, звичайно, високий процент на інвестований капітал. Цей високий прибуток спонукає вкладників спрямовувати ресурси з інших галузей в дану, і нові фірми з'являються на ринку. Поступове розширення виробництва, пов'язане з появою нових фірм, зміщує вправо криву ринкової пропозиції. При цьому обсяг реалізації на ринку зростає, а ринкова ціна товару падає. Рисунок 5.18 ілюструє це положення.

У правій частині рисунка 5.18 крива пропозиції змішується від S1 до S2, що змушує ціну знижуватися з ці (40 грн.) до Ц1 (30 грн.). В лівій частині рисунка 5.18, що ілюструє поведінку окремої фірми, довгострокова крива витрат на одиницю продукції торкається лінії ціни при обсязі виробництва q2/ В результаті, фірма отримує нульовий прибуток.

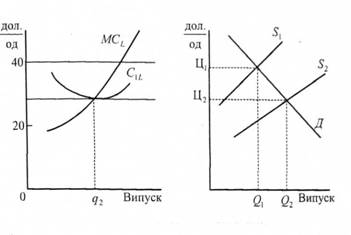
а - фірма; б - галузь; Д - лінія попиту

Рисунок 5.18. Графік довгострокової конкурентної переваги

Фірма вступає на ринок, розраховуючи заробити прибуток, і залишає справу у випадку збитків. За довгострокової рівноваги фірми отримують нульовий прибуток. Чому ж вони вступають у справу, якщо знають, що врешті решт вони одержать нульовий прибуток? Відповідь полягає в тому, що потрібно чимало часу, щоб досягти довгострокової рівноваги, але впродовж короткого відрізку часу фірма може одержати значний прибуток (або зазнати збитків).

Перша фірма, що вступає в прибуткову справу, може отримати значно більший короткостроковий прибуток для своїх вкладників капіталу, ніж фірми, що вступають у справу пізніше. Аналогічне, фірми, що виходять із неприбуткової галузі промисловості першими, можуть заощадити інвесторам значну кількість грошей. Таким чином, концепція довгострокової рівноваги пояснює нам, в якому напрямку, вірогідніше за все, буде діяти фірма. Висновок відносно кінцевого нульового прибутку не повинен збивати з путті менеджерів, винагорода яких залежить від короткострокового прибутку, ще отримує фірма [ 51 ].

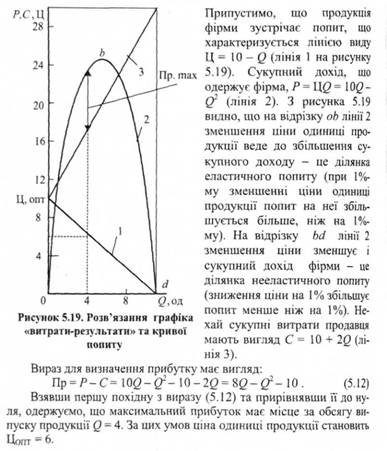
РОЗВ'ЯЗАННЯ ГРАФІКА "ВИТРАТИ-РЕЗУЛЬТАТИ" ТА КРИВОЇ ПОПИТУ