Прийняття управлінських рішень - Петруня Ю.Є. - Розділ 8. Методи прогнозування розробці управлінських рішень

8.1. Кількісні методи прогнозування

Розробка управлінського рішення в багатьох випадках передбачає врахування того, що може відбутися в зовнішньому середовищі організації в майбутньому. В управлінському рішенні відбивається комбінація бачення поточної ситуації та уявлення про можливі майбутні зміни. Чим точніше управлінець зможе передбачити зовнішні і внутрішні умови майбутнього, тим вища ймовірність досягнення запланованих результатів. Прогнозування може розглядатись як важливий інструмент "більш точного налаштування" бачення майбутніх змін. Без прогнозування, без уявлення майбутнього розвитку події неможливо прийняти ефективне управлінське рішення.

Прогнозування - процес передбачення майбутнього стану, перспектив змін певного явища чи процесу. Мета прогнозування - отримання науково обґрунтованих варіантів тенденцій розвитку показників, що характеризують відповідні явища та процеси і впливають на прийняття управлінського рішення та на управління організації в цілому.

Економічне прогнозування можна зарахувати до основних галузей прогнозування. Його результати використовуються для розробки управлінських рішень в інвестиційній, маркетинговій, збутовій та інших сферах діяльності. Оскільки будь-яке управлінське рішення за своєю суттю прогнозне, то прогнозування створює фундаментальну основу управлінської діяльності в будь-якій сфері. Роль прогнозування в менеджменті нерозривно пов'язана з роллю прийняття рішень, а прийняття управлінських рішень - вузлова процедура циклу управління в діяльності менеджерів усіх рівнів. Нерозривний зв'язок рішення і прогнозування пояснюється тим, що ще до прийняття рішення необхідно: отримати інформацію, обробити її, провести аналіз, подати у зручній формі. Прогнозування відбувається одночасно на базі: інтуїтивної інформації з використанням уяви; предметної інформації та логіки; кількісних даних і математичних методів.

На практиці використовують різні методи прогнозування. На вибір методу впливають, зокрема, такі фактори:

- форма прогнозу;

- період прогнозування;

- доступність, відповідність і придатність даних;

- точність прогнозу;

- особливості об'єкта прогнозування;

- витрати на прогнозування.

Методи прогнозування мають відповідати таким вимогам: поєднання суб'єктивної цінності й об'єктивної значущості оцінок; чітке застосування оцінок, яке не допускає різних тлумачень щодо вибору методів; можливість накопичення статистичної інформації та її використання для прогнозування.

За оцінкою спеціалістів, нараховується більш ніж 150 методів прогнозування, хоча на практиці використовується набагато менше.

Існує багато підходів до класифікації методів прогнозування. Зокрема, ці методи поділяють на кількісні та якісні.

Кількісні методи базуються на інформації, яку можна одержати, знаючи тенденції зміни параметрів або маючи статистично достовірні залежності, що характеризують виробничу діяльність об'єкта управління. Прикладами цих методів є аналіз часових рядів, причинно-наслідкове (каузальне) моделювання тощо.

Якісні методи ґрунтуються на досвіді, інтуїції, експертних оцінках фахівців у галузі прийняття рішень, наприклад методи експертних оцінок, думка журі (усереднення думок експертів у релевантних сферах), моделі очікування споживача (результат опитування клієнтів), думки досвідчених торгових агентів. На рис. 8.1 показано загальну схему вибору методів прогнозування.

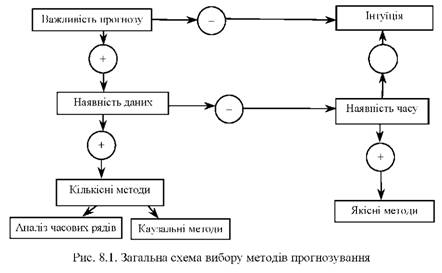
Розглянемо кількісні методи прогнозування більш детально.

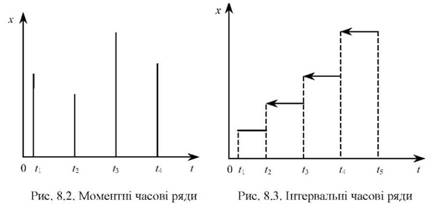
1. Аналіз часових рядів. Часові ряди бувають моментні й інтервальні. У перших у відповідні моменти часу (^) отримуються значення деякого параметра (хі).

Для інтервальних часових рядів у відповідні інтервали часу ^) значення деякого параметра (х) має сталі значення. Моментні й інтер-вальні часові ряди задаються графічно (рис. 8.2-8.3).

Для прогнозування з використанням аналізу часових рядів потрібна достатня кількість інформації в минулому для передбачення майбутнього стану. Попередня інформація дає можливість визначення тенденції розвитку процесу.

Методи прогнозування на основі аналізу часових рядів не можуть ураховувати деякі втручання ззовні в процес з можливими випадковими чи невипадковими відхиленнями. Чим більше даних і менший період прогнозу, тим точніший прогноз.

Для аналізу часових рядів використовують методи: 1) плинної середньої та зваженої плинної середньої; 2) експоненціального згладжування; 3) екстраполяції на основі аналітичних показників; 4) екстраполяції тренду.

Метод плинної середньої. Ґрунтується на ідеї обчислення середньої величини для проміжку, який є сумою кількох послідовних проміжків із заданими на їх кінцях рівнями ряду. Новий ряд, рівні якого - це певним чином усереднені значення рівнів вихідного ряду, має менші відхилення від закономірних значень досліджуваного показника.

Щоб використати плинну середню як показник тенденції та відповідно прийняти рішення, слід з'ясувати часовий проміжок, за який треба розрахувати середню, і визначити потрібний момент для ефективного виходу на ринок цінних паперів з інвестиційним рішенням.

Обчислення прогнозованої величини за методом плинної середньої базується на використанні такої залежності:

~і = уі + ^ і Ауі + ^ і-АУі-і + ^ г-2 Ауі-2 + - + ^ Нй-і) Ауі-("-і)'

де Ауі - ланцюговий абсолютний приріст, який визначається за формулою:

4у = уі ~yi-l,

де уп - кінцеве значення рівня динамічного ряду;

уі - умовно прийнятий ( і -й) рівень динамічного ряду; п - кількість елементів динамічного ряду. Коефіцієнт плинної середньої Хі розраховується так:

п

де п - кількість років передісторії;

і - число, яке означає послідовний натуральний ряд передісторії, починаючи з останнього.

Коефіцієнт Р визначається за табл. 8.1.

Таблиця 8.1

Особливістю методу плинної середньої є те, що рівень показників, який ближчий до прогнозованого періоду, більше впливає на значення прогнозованих показників порівняно з віддаленими періодами. Досягається це завдяки коефіцієнту X.

Метод зваженої плинної середньої. Ітераційна формула обчислення прогнозованої величини /п в наступні моменти часу:

N

~ 2 ™п-іуп-і

~ = М-

■>п N '

2 ^п-г

де уп_і - це значення прогнозованої величини в попередні N моменти

часу (значення уп _ 1 відповідають моментам часу їп _ 1, а значення /п - моментам часу іп);

уїп - 1 - вагові коефіцієнти, які відповідають значенням уп - 1 і котрі тим більші, чим ближчі відповідні моменти часу 4 - 1 до часу 4.

Метод експоненціального згладжування. Сутність методу полягає в тому, що кожний елемент часового ряду згладжується за допомогою зваженої плинної середньої, причому її вага зменшується в міру віддалення від кінців ряду. Крім того, в прогнозі беруть участь усі п відомих значень уп_і ( і = 1, п -1) часового ряду

~п+1 = ауп + а(1 - а)уп-1 + а(1 - а)2 уп-1 + ... ,

де а - параметр згладжування (0< а <1).

Ітераційна формула обчислення прогнозованої величини ~п+1 за методом експоненційного згладжування має вигляд:

~п+1 = иуп + "(1" <*) у*.

Для вищерозглянутих методів простої плинної середньої робиться адаптація числа N, зваженої плинної середньої - адаптація N і вагових коефіцієнтів м>п - і, а для експоненціального згладжування - адаптація параметра а. Для адаптації перелічених параметрів використовуються раніше отримані статистичні дані.

Метод екстраполяції на основі аналітичних показників. Цей метод передбачає дослідження й аналіз основних показників ряду. Прогнозована оцінка рівня ряду розраховується за допомогою середнього абсолютного приросту або середнього коефіцієнта зростання. Перевагою цього методу є відносна простота прогнозування, наявність невеликої кількості даних, а до недоліків належить те, що метод не дає можливості сформувати довірчий інтервал прогнозованої величини, а також неможливість отримання якісного прогнозу за наявності нерівномірного зростання чи спадання часових рядів.

Значення прогнозованої величини на основі середнього абсолютного приросту обчислюється за формулою:

де уп - кінцеве значення рівня динамічного ряду;

Ау - середній абсолютний приріст;

Т - величина горизонту прогнозу (Т = 1; 2; 3...).

Значення прогнозованої величини на основі середнього коефіцієнта зростання таке:

Уп+Т = уп o кР ,

де кр - середній коефіцієнт зростання.

Середній абсолютний приріст визначається за формулою:

дУ = Уп ~ Уі.

п -і

Середній коефіцієнт зростання визначається за формулою:

~кр = ^ o

де уі - початкове значення рівня динамічного ряду; уп - кінцеве значення рівня динамічного ряду; п - кількість елементів ряду динаміки.

Метод екстраполяції тренда. Тренд - це тенденції зміни певного показника в часі. При екстраполяції тренда за допомогою рядів динаміки виконують такі етапи: роблять попередній аналіз даних, формулюють набір моделей, оцінюють їх параметри, перевіряють їх адекватність, вибирають найкращу модель, роблять точкове та інтервальне прогнозування, виконують верифікацію прогнозу.

Особливості прогнозування за трендом:

- прогнозування за трендом припустиме зі збереженням основної тенденції та умов розвитку і неприпустиме в разі настання стрибкоподібних, революційних змін;

- прогноз на основі трендів охоплює всі фактори в неявному й узагальненому вигляді (на відміну від багатофакторної регресійної моделі, де кожен фактор має числову характеристику міри свого власного впливу).

За даними ряду динаміки будується функція у = /(і), яка аналітично виражає залежність значень досліджуваної величини У від часу і і називається трендовою кривою або лінією тренда. Існує багато різних типів кривих, які використовуються на практиці як лінії тренда.

Рівняння тренда може бути описане такими залежностями:

а) лінійна (використовується для опису величини, яка збільшується або зменшується з постійною швидкістю):

у = а + Ьї;

б) квадратична (використовується для опису величин, що поперемінно зростають і зменшуються):

у = а + Ьх + сї2;

в) степенева:

у = аі ;

г) експоненціальна (використовується, якщо швидкість зміни даних безперервно зростає):

bt

y = ae ;

д) показникова:

y = abt;

е) крива Гомперца:

y = kab, де b< 1;

є) логістична:

k

У " 1 + ae-bt ;

ж) гіперболічна:

b

y = a ч-;

де а і b - константи, t - змінна, e - основа натурального логарифма.

Використання лінії тренду того або іншого вигляду визначається характером вихідного ряду динаміки. Для знаходження коефіцієнтів трендових кривих використовують метод найменших квадратів. Для обраної трендової кривої ~~ = yt (a1, a2,...) будується функція

F(a1,a2,...) = 2(yЎ - yt) , яка мінімізується. Для цього частинні похі-

7=1 '

. dF 8F

дні: -, -, ... - прирівнюються до нуля. Утриману систему рівнянь розв'язують стосовно невідомих значень параметрів а1, а2, ... . Наприклад, для рівняння прямої yt = a0 + a1t система рівнянь для знаходження значень параметрів a0, а1 матиме такий вигляд:

( n n

nao + l1t' h = Л y';

Нелінійні тренди попередньо зводять до лінійної функції відповідними математичними перетвореннями, після чого застосовують метод найменших квадратів для визначення невідомих параметрів а1, а2, ... рівняння. Розглянемо деякі нелінійні залежності.

Для квадратичної залежності ~ = а + Ьї + сі2 система рівнянь, з якої розраховують коефіцієнти а, Ь, с, матиме вигляд:

па + 1 Ь + 1 2Х2 |с = 2 уі ,

Степенева функція ~ = аїЬ зводиться до лінійної, якій відповідає система рівнянь:

ґ п Л п

п8 + 1 2 іп ^ )Ь = 2 іп уі,

де я = іп а, а = е8.

Показникова функція ~ = аЬ? для отримання коефіцієнтів а, Ь зводиться до такої системи рівнянь:

п8 + ^ Ьі ^ / = уі ,

[ 2?і ] 8 + [ 2?2 у = 2?і іп уі ,

де 8 = іп а, а = е8, / = іп Ь, Ь = .

Гіперболічній залежності ~ = а + - відповідатиме така система рівнянь, з якої знаходять коефіцієнти а, Ь.

Г ґ

І п 1 І п

па + Ь = ^ уі ,

І і=1 ?і ) і=1

( п 1 А ( п 1 Л п у

2- а + £- Ь = £А.

Екстраполяція за допомогою часових рядів передбачає такі етапи: попередній аналіз даних, формулювання набору моделей, оцінка параметрів моделей, перевірка адекватності моделі, вибір найкращої моделі, точкове й інтервальне прогнозування, верифікація прогнозу.

Якість (адекватність) і щільність побудованого тренда можна оцінити за допомогою показників.

- У)2

1. Коефіцієнт детермінації: R2 =--,

т -y )2

- 1 "

де y = -^Уі - середнє значення величини Y.

П і=1

Коефіцієнт детермінації R може набувати значення від 0 - повна неадекватність, до 1 - повна адекватність побудованої трендової кривої. Чим R2 ближчий до 1, тим надійнійша лінія тренда.

2. Коефіцієнт кореляції є мірою щільності зв'язку: t < 0,5 - зв'язок слабкий; 0,5 < t < 0,7 - зв'язок помірної щільності (середній), т > 0,7 - зв'язок щільний (сильний).

3. Середня абсолютна похибка апроксимації:

д -у yt -~t

^абс - 2-, ■

П

4. Середня відносна помилка апроксимації:

£ = - ^Jyi_i2yJ .100%. П yt

5. Середнє квадратичне відхилення:

V П

Чим менше значення показників 3-5, тим вища якість трендової моделі.

Підбираючи лінію тренда до даних за допомогою Excel, можна автоматично розраховувати значення R та відобразити рівняння лінії тренда на діаграмі.

Прогнозоване значення показника Г-період можна отримати, підставляючи значення 7-періоду в розраховане чи автоматично виведене рівняння тренда.

Точковий прогноз здійснюється шляхом екстраполяції попередньо знайденої трендової кривої yt на час Т, тобто прогнозоване значення ут ознаки Yобчислюється за формулою yT = f (T).

Інтервальний прогноз - це інтервал значень величини Y, який із заданою ймовірністю повинен містити її майбутнє значення. Такий інтервал називається надійним (або довірчим), а відповідна ймовірність - надійною (або довірчою). Наприклад, інтервальний прогноз на наступний часовий інтервал визначається лівою у' = yT -1а (k) o S та правою

У = Ут + ta (k)' Sр межами, ta(k) - коефіцієнт довіри (або довірче число), який знаходиться за таблицями критичних точок розподілу Стьюдента, залежно від кількості степенів вільності k = n - m та рівня значущості a; m - кількість параметрів трендової кривої; S3 - регре-

сійне середнє квадратичне відхилення S3 = ^|ТХуі ~ Уі )2 jk1 ~ m)..

2. Каузальні методи прогнозування використовуються тоді, коли прогнозована величина залежить від великої кількості складних факторів, які можна використовувати тільки за наявності обчислювальної техніки та відповідного програмного забезпечення (наприклад, пакетів: Statistica, SPSS, Excel, Mathcad, Mathlab, Maple тощо).

Каузальні методи прогнозування поділяються на такі:

1) багатовимірні регресійні моделі, які є узагальненням вищенаве-деного методу проекціювання тренда, коли враховується не один, а кілька факторів і залежності можуть бути як лінійні, так і нелінійні;

2) економетричні моделі - це складні моделі, які враховують велику кількість параметрів і розв'язуються як екстремальні задачі або зводяться до розв'язання великих систем лінійних або нелінійних рівнянь;

3) комп'ютерна імітація.