Прийняття управлінських рішень - Петруня Ю.Є. - Висновки

Ризик - це можливість виникнення несприятливого випадку. Під цим розуміють імовірність втрати організацією своїх ресурсів, недоот-римання доходів або отримання додаткових збитків у результаті певної діяльності, інші негативні наслідки.

Ризики можна поділити на два види: динамічні та статичні. Динамічний ризик залежить від зовнішніх умов, наприклад зміни вартості товарних запасів як результату зміни курсу валют. Це можливо внаслідок економічних, політичних та інших змін. Статичний ризик можливий через дії самої організації (рівень кваліфікації персоналу, технічного забезпечення тощо). Під якісним ризиком розуміють різні види ризику, а під кількісним - можливі значення втрат внаслідок відповідного якісного ризику.

Під час дослідження ризику необхідно послідовно виконати такі дії: 1) виділити об'єктивні та суб'єктивні фактори, що впливають на конкретний вид ризику; 2) зробити аналіз виявлених факторів; 3) оцінити можливість того або іншого проекту з урахуванням різних видів ризику; 4) встановити допустиму верхню межу рівня ризику; 5) забезпечити заходи зниження ризику. Існують чотири способи управління ризиком: а) розподіл ризику між усіма учасниками проекту; б) страхування; в) резервування коштів; г) диверсифікація.

Розглянемо визначення міри ризику. Припустімо, що є m стратегій та n станів "природи". Задана матриця прибутковості A = (atJ )mxn, де

atJ - прибуток від реалізації 7-ї стратегії за j-ro стану "природи", qy -

ймовірність настання j-ro стану природи. Використовуються різні способи обчислення міри ризику найбільш важливих показників діяльності компанії або підприємства, наприклад за показниками варіації.

1. За дисперсією Di = 2z,aij ~ Mi [qj або Di = 2 aiflj - Mi ,

i = 1, m, Mi = 2ayqj. Mi математичні сподівання ефективності i-ї стратегії, i = 1, m. Чим більша дисперсія, тим більший ризик.

2. За середнім квадратичним відхиленням aЎ = i = 1, m. Чим менше середнє квадратичне відхилення, тим надійніша стратегія.

3. За коефіцієнтом варіації Vi = -----, i = 1, m. Чим більше значення коефіцієнта варіації, тим більш ризикована стратегія.

4. За семіваріацією SVЎ = £осЎ4Ў(О/ ~MЎ) , де а j індикатор відхи-

j=i _

лення від трогових значень MЎ, j = 1, n, де MЎ - математичне сподівання ефективності z'-ї стратегії. Для розрахунків додатної семіваріації

SVЎ+ беруть a j = 1, якщо ьj > MЎ, і а j = 0, якщо ьj < MЎ,

i = 1, m, j = 1, n. Додатна семіваріація SVЎ+ математичним сподіванням квадратів відхилень значень прибутку або від математичного сподівання ефективності 7-ї стратегії MЎ, які більші за нього, Ў = 1, m. Тобто чим більший цей показник, тим більший очікуваний від реалізації відповідної стратегії прибуток. У розрахунках від'ємної семіваріації SVЎ~ навпаки - а ■ = 1, якщо ьj < MЎ, і а ■ = 0, якщо

aЎj > MЎ, Ў = 1, m, j = 1, n. Від'ємна семіваріація SVЎ_ є сумою квадратів відхилень значень прибутку або від математичного сподівання ефективності 7-ї стратегії MЎ, які не перевищують його, Ў = 1, m. Тобто чим менша від'ємна семіваріація, тим менші прогнозовані втрати від відповідної стратегії.

5. За семіквадратичним відхиленням SSVЎ =^jSVЎ. Очевидно, що розраховуються SSV і+ і SSVЎ ~ : SSVЎ+ ={SSv+ SSVr ={SSvt, Ў = 1^.

SSV~ _

6. За коефіцієнтом ризику KrЎ =-'-, Ў = 1, m. Чим менший кое-

ssvЎ

фіцієнт ризику, тим менший ризик вибору стратегії.

Розглянемо інтервальну оцінку ефективності стратегій. Для ін-

тервальної оцінки розраховують граничну похибку AЎ = 7 Ў, якщо

Vn

t у ■ sЎ

n > 30, i AЎ = ' , якщо n < 30, де oЎ - середнє квадратичне відхи-

пг

лення, sЎ - виправлене середнє квадратичне відхилення: sЎ = <3ЎJ-,

V n -1

і = 1, m, t,f = t(а = 1 - у, v = n -1) знаходиться за таблицею критичних

точок розподілу Стьюдента для двосторонньої критичної області залежно від надійності у та обсягу вибірки n, а - рівень значущості, v - кількість степенів вільності, у - надійність того, що фактичний прибуток перебуватиме у відповідному надійному інтервалі. Чим менша гранична похибка (граничне відхилення), тим безпечніша і надійніша стратегія. Додавши та віднявши граничну похибку Аі до математичного сподівання ефективності і-ї стратегії Mj, отримаємо граничні межі, в яких коливатиметься фактичний прибуток за кожною стратегією: ajmax = Mj + Аі, ajmin = Mj - Aj, і = 1, m. У випадку коли aj min набуває від'ємного значення, замість очікуваного прибутку маємо обсяг очікуваних витрат.

Для оцінки ризику використовують розмах варіації, що розраховується на основі граничних меж atmin та atmax : Яі = atmax - atmin,

і = 1, m. Чим більший розмах варіації, тим більш ризикована стратегія.

Розглянемо визначення ступеня ризику. Один з його методів ґрунтується на оцінці можливих втрат від реалізації стратегії як співвідношення мінімального значення ефективності і-ї стратегії aimin до математичного

сподівання ефективності і-ї стратегії: Ксрі = ьlmin , і = 1, m. Якщо

і min

Ксрі > 0, то ризик припустимий, якщо -0,3 < Ксрі < 0, то вважають, що ризик виправданий, а якщо ж Ксрі < -0,3, то ризик оцінюють як

критичний або неприйнятний, і = 1, m.

Припустімо, розглядаються два проекти А та В. Для кожного проекту обчислюються математичне сподівання, наприклад прибутку: mA,

mB, та його середнє квадратичне відхилення: аA, аB. Проект тим кращий, чим більше математичне сподівання прибутку і чим менше середнє квадратичне відхилення. Якщо mA > mB та аA > аB або mA < mB та аA < аB, не можна однозначно сказати, який проект кращий. Тоді визначаються відносні значення показників або відсотки, за якими вибирається той проект, для якого покращання за одним показником перевищує погіршення за другим. Для візуального сприйняття координати показників проектів а та m наносяться на площину, що часто допомагає вибрати кращий проект (рис. 9.2).

Розглянемо позиційну гру на прикладі моделювання процесу входження на ринок. Наприклад, перша компанія вже випускає певний товар, друга компанія бачить, що перша отримує великі прибутки, й аналізує можливості входження на цей ринок зі своїм товаром.

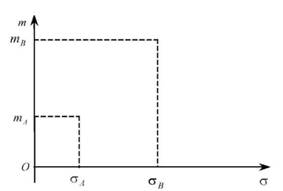
Рис. 9.2. Показники проектів

Перша компанія за випуск товару отримує 12 одиниць прибутку (в існуючих умовах). Можливі такі стратегії дій компанії: для першої - зберегти обсяги виробництва, зменшити обсяги виробництва; для другої - організувати нове виробництво, відмовитися від нової ідеї.

У табл. 9.1 показані можливі прибутки, збитки компаній (у дужках).

Таблиця 9.1

вихідні дані, млн грн

Табл. 9.1 відповідає граф (дерево рішень), що часто використовується у розв'язуванні позиційних ігор (рис. 9.3).

Рішення І компанії Рішення II компанії

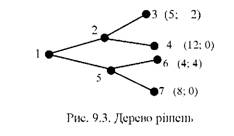
Рішення І компанії: 1-2 - зберегти обсяги виробництва, 1-5 - зменшити їх. Рішення II компанії: 2-3 - організувати нове виробництво, 2-4 - утриматися, 5-6 - організувати нове виробництво, 5-7 - утриматися. Стратегія І компанії "зберегти обсяги виробництва" домінуюча, і вона за такої стратегії одержить більший прибуток, ніж за варіантом "зменшити обсяги виробництва", незалежно від стратегії II компанії. Враховуючи таку ситуацію, II компанія змушена утриматися від вступу до ринку.

Існує така послідовність розв'язування задач з використанням дерева рішень: 1) формулювання задачі, визначення найбільш суттєвих факторів і отримання відповідної інформації; 2) побудова дерева рішень; 3) оцінка ймовірностей станів середовища; 4) обчислення виграшів (програшів) за різних комбінацій альтернатив; 5) остаточний вибір розв'язання задачі.

Отже, дерево рішень відображає ієрархічність і ранжування цілей, що мають такі ознаки: а) співзалежність, наприклад тактичні цілі залежать від стратегічних; б) розгортання за часом, рівнем і складом; в) ранжування цілей за важливістю.

Дерева рішень можна ефективно використовувати для розв'язування важливих багатоаспектних управлінських проблем.

Висновки

1. Теорія ігор - це розділ дослідження операцій з математичними моделями прийняття оптимальних рішень в умовах конфлікту.

2. Стратегічні (матричні) ігри виникають під час розв'язування різних задач економіки, коли інтереси партнерів мають протилежний характер.

3. Антагоністична модель у багатьох випадках є достатньо грубим відображенням реальних конфліктів, у яких інтереси сторін хоча й різні, але можуть бути непротилежними, кількість гравців може бути більше двох, а сума виграшів - не рівна нулю.

4. У теорії "ігор з природою" залежно від інформації розглядають дві ситуації: "прийняття рішень в умовах ризику" - відомі ймовірності або невідомі, але є дані щодо їх відносних значень, або встановлюються за допомогою експертів; "прийняття рішень в умовах невизначеності" - ймовірності можливих станів природи невідомі та немає ніякої можливості отримати таку інформацію.

5. Під ризиком розуміють імовірність втрати організацією своїх ресурсів, недоотримання доходів або отримання додаткових збитків у результаті певної виробничої або фінансової політики. Використовуються різні способи обчислення міри ризику найбільш важливих показників діяльності фірми або підприємства.

6. Дерево рішень - це графічне відображення послідовності рішень і станів середовища із зазначенням відповідних імовірностей (якщо вони відомі) та виграшів (програшів) для довільних комбінацій альтернатив. Граф (дерево рішень) часто використовується для розв'язування позиційних ігор.