Моделі і методи прийняття рішень в аналізі та аудиті - Гаркуша Н.М. - 14.3.2. Методи екстраполяції

Одним із найбільш поширених методів короткострокового прогнозування економічних явищ є екстраполяція.

Термін "екстраполяція" має кілька тлумачень. У широкому значенні екстраполяція - це метод наукового дослідження, що полягає в поширенні висновків, отриманих зі спостережень за однією частиною явища, на іншу його частину. У вузькому значенні - це визначення по ряду даних функції інших її значень поза цим рядом.

Екстраполяція полягає у вивченні сформованих у минулому і сьогоденні стійких тенденцій економічного розвитку і перенесення їх на майбутнє.

Мета такого прогнозу - показати, до яких результатів можна дійти в майбутньому, якщо рухатися до нього з тією самою швидкістю або прискоренням, що й у минулому.

Прогноз визначає очікувані варіанти економічного розвитку виходячи з гіпотези, що основні фактори і тенденції минулого періоду збережуться на період прогнозу або що можна обґрунтувати і врахувати напрямок їхніх змін у розглянутій перспективі. Подібна гіпотеза висувається виходячи з інертності економічних явищ і процесів.

У прогнозуванні екстраполяція застосовується при вивченні часових рядів.

Екстраполяцію в загальному вигляді можна представити у вигляді певного значення функції

де у, - прогнозоване значення рівня ряду динаміки; І - період упередження;

уІ - рівень ряду, прийнятий за базу екстраполяції; а - параметри рівняння тренду.

Залежно від особливостей зміни рівнів у рядах динаміки методи екстраполяції можуть бути простими і складними (рис. 14.7).

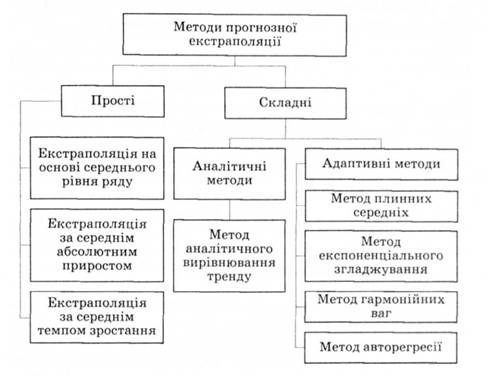
Рис. 14.7. Групування методів прогнозної екстраполяції

Прості методи екстраполяції ґрунтуються на припущенні відносної сталості в майбутньому абсолютних значень рівнів, середнього рівня ряду, середнього абсолютного приросту, середнього темпу зростання.

Розглянемо докладніше названі методи екстраполяції.

При екстраполяції на основі середнього рівня ряду використовується принцип, при якому прогнозований рівень дорівнює середньому значенню рівнів ряду в минулому, тобто

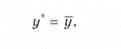
У такому випадку екстраполяція дає прогностичну точкову оцінку. Точний збіг цих оцінок з фактичними даними - явище малоймовірне. Отже, прогноз має бути у вигляді інтервалу значень. Довірчий інтервал прогнозу для середньої при невеликому числі спостережень знаходиться за формулою

де *о - табличне значення £ - критерію Стьюдента з п - 1 ступенями вільності і рівнем імовірності р; о - середнє квадратичне відхилення.

У свою чергу середнє квадратичне відхилення для вибірки дорівнює:

де уІ - поточний рівень ряду динаміки; п - число рівнів ряду динаміки.

Отриманий довірчий інтервал враховує невизначеність, пов'язану з оцінкою середньої величини, і його застосування для прогнозування збільшує ступінь надійності прогнозу. Але недоліком розглянутого підходу є те, що довірчий інтервал не пов'язаний з періодом упередження.

Екстраполяція за середнім абсолютним приростом може бути здійснена тоді, коли вважати загальну тенденцію розвитку явища лінійною.

Для обчислення прогнозного значення рівня необхідно визначити середній абсолютний приріст Л. Потім, знаючи рівень ряду динаміки, прийнятий за базу екстраполяції уп, записати екстраполяційну формулу

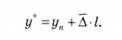
Екстраполяція за середнім темпом зростання може бути здійснена, коли є підстави вважати, що загальна тенденція ряду динаміки характеризується показовою кривою. Прогнозований рівень ряду в цьому випадку визначається за формулою

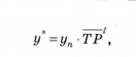
де ТР - середній темп зростання, який розраховано за формулою середньої геометричної.

Довірчий інтервал прогнозу за середнім темпом зростання може бути визначений лише в тому випадку, коли середній темп зростання розраховується за допомогою статистичного оцінювання параметрів експоненціальної кривої.

Усі три розглянуті методи екстраполяції тренду є найпростішими, але водночас і найбільш наближеними.

Складні методи екстраполяції передбачають виявлення основної тенденції, тобто застосування статистичних формул, що описують тренд. Методи цієї групи можна розділити на два основні типи: аналітичні (криві зростання) й адаптивні.

В основу аналітичних методів прогнозування (кривих зростання) покладений принцип отримання за допомогою методу найменших квадратів оцінки детермінованої компоненти, що характеризує основну тенденцію.

Адаптивні методи прогнозування засновані на тому, що процес реалізації їх полягає в обчисленні послідовних у часі значень прогнозованого показника з урахуванням ступеня впливу попередніх рівнів. До них належать методи плинної та експоненціальної середніх, метод гармонійних ваг, метод авто-регресії.

Метод аналітичного вирівнювання тренду (метод найменших квадратів) може бути застосований тільки в тому випадку, коли розвиток явища досить добре описується побудованою моделлю й умови, що визначають тенденцію розвитку в минулому, істотно не зміняться у майбутньому. При дотриманні цих вимог прогнозування здійснюється шляхом підстановки в рівняння тренду значень незалежної змінної £, що відповідає величині періоду упередження.

Процедура розробки прогнозу щодо використання аналітичного вирівнювання тренду складається з таких етапів:

1) вибір форми кривої, що відображає тенденцію;

2) визначення показників, що кількісно характеризують тенденції змін;

3) оцінка вірогідності прогнозних розрахунків.

Вибір форми кривої можна здійснювати на основі побудови графіка, загальний вигляд якого, як правило, дає змогу встановити:

а) чи має динамічний ряд показника чітко виражену тенденцію;

б) якщо так, то чи ця тенденція плавна;

в) який характер тенденції.

Відповідаючи на ці питання, необхідно пам'ятати, що зовнішня простота графіка хибна. Будь-яке динамічне завдання набагато складніше від статичного й кожна точка кривої є результатом зміни явища як у просторі, так і в часі.

У зв'язку з цим для підвищення обґрунтованості й вірогідності вирівнювання з метою більш точного виявлення наявної тенденції необхідно провести варіантний розрахунок за кількома аналітичними функціями й на основі експертних і статистичних оцінок визначити кращу форму зв'язку.

На другому етапі необхідно визначити параметри рівняння зв'язку. Для їх знаходження використовують метод найменших квадратів. У цьому випадку вирівнювальна функція буде займати таке положення серед фактичних значень показників, при якому сумарне відхилення точок від функції буде мінімальним.

Достовірну й обґрунтовану оцінку отриманим результатам можна дати, використовуючи такі статистичні показники, як середній коефіцієнт зростання, загальна і залишкова дисперсія, коефіцієнт кореляції, індекс кореляції, коефіцієнт кореляції вихідного ряду і ряду відхилень визначеного за різницею фактичних і вирівняних за будь-якою аналітичною функцією даних.

Для перевірки гіпотези про наявність або відсутність автокореляції використовують таблиці з критичними значеннями коефіцієнта автокореляції при різних рівнях значимості. Якщо табличне значення коефіцієнта автокореляції вище від фактичного, то можна стверджувати, що автокореляція відсутня або усувається, а отже, можна використовувати формули для імовірнісної оцінки значень, які прогнозуються за цими точками.

Приклад 14.1

Розглянемо використання методу аналітичного вирівнювання за даними діяльності TOB "Браво" м. Харкова, наведеними в табл. 14.4.

Таблиця 14.4. Динаміка товарообороту TOB "Браво"

Для прогнозу були обрані такі функції, як лінійна, логарифмічна, поліноміальна, ступенева та експоненціальна.

Наочне зображення коливань обсягу товарообігу за вказаними аналітичними функціями наведено на рис. 14.8.

Статистичні оцінки розглянутих аналітичних функцій наведені в табл. 14.5 (с. 539).

Як показують дані таблиці, не всі обрані аналітичні функції добре вирівнюють вихідний динамічний ряд. Про це свідчить значення коефіцієнта (індексу) кореляції. Для прогнозування, тобто продовження сформованої тенденції на найближчу перспективу, можуть бути використані тільки ті функції, для яких коефіцієнт (індекс) кореляції перевищує 0,7. До таких належать лінійна, експоненціальна й поліноміальна функції. Остання має найбільший коефіцієнт кореляції, який дорівнює 0,847, і найменшу величину залишкової дисперсії.

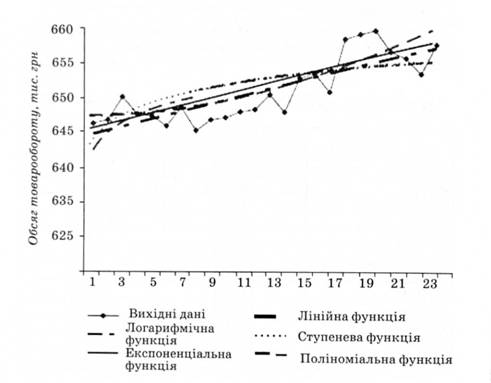
Рис. 14.8. Вихідні та вирівняні за аналітичними функціями значення обсягу товарообороту TOB "Браво"

Отже, найбільш прийнятною формою аналітичної функції для прогнозування є поліноміальна функція, яка представлена таким рівнянням:

Підставивши в отримане рівняння значення періодів упередження, визначаємо прогнозне значення обсягу товарообороту на наступні три місяці: у25 = 654,83; у = 655,93; у"--657,07 тис.грн. 26 27

Таблиця 14.5. Характеристики вирівнювальних функцій для динамічного ряду товарообороту

Ймовірність того, що прогнозований економічний показник у заданий момент часу буде дорівнювати значенню, яке відповідає точковому прогнозу, практично дорівнює нулю. Тому до точкового прогнозу визначаються границі можливої зміни прогнозованого значення показника - довірчий інтервал за формулою

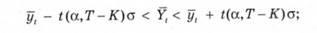
де * (а, Т - 20 - табличне значення розподілу Стьюдента зТ-д ступенями вільності й рівнем значимості а;

а - середньоквадратична помилка прогнозу.

Середньоквадратична помилка прогнозу обчислюється за формулою

де п - число рівнів динамічного ряду;

р - число параметрів у рівнянні прогнозу;

Зазначимо, що до отриманих при прогнозуванні оцінок довірчих інтервалів слід ставитися з обережністю. Це пов'язано зі специфікою динамічних рядів. Специфічність їх полягає в тому, що збільшення числа спостережень у статичній сукупності дає змогу одержати більш точні характеристики цієї сукупності, тоді як аналогічне подовження ряду динаміки не завжди приводить до подібних результатів, особливо в тих випадках, коли ряди динаміки використовуються для прогнозування. Ця обставина пов'язана з тим, що інформаційна цінність рівнів втрачається в міру їхнього віддалення від періоду упередження, тобто значення рівнів ряду динаміки при прогнозуванні нерівноцінне. Тому параметри рівнянь апроксимуючих кривих зростання можуть мати похибки і змінювати свої оцінки при виключенні частини членів ряду або додаванні нових членів ряду динаміки, що відбивається на точності розрахункових значень рівнів ряду динаміки. Крім того, параметри моделей тренду, отримані методом найменших квадратів, залишаються незмінними протягом усього розглянутого періоду. На практиці часто трапляються випадки, коли параметри моделей змінюються, а процедури, що згладжують, за допомогою методу найменших квадратів не можуть помітити такі зміни. Тому більш ефективними виявляються адаптивні методи, у яких значимість рівнів ряду динаміки зменшується в міру їхнього віддалення від прогнозованого періоду. До них належать: метод плинних середніх, метод експоненціального згладжування, метод гармонійних ваг та інші, що входять до класу адаптивних методів.

Часто ряди динаміки характеризуються різкими коливаннями показників за роками. Такі ряди, як правило, мають слабкий зв'язок з часом і не виявляють чіткої тенденції зміни. У цьому випадку метод аналітичного вирівнювання малоефективний, тому що вірогідність розрахунків різко падає. Довірчі границі прогнозу інколи виявляються ширшими за коливання показника в ряді динаміки.

При прогнозуванні на основі часових рядів, що дуже коливаються, можна використовувати метод плинних середніх, за допомогою якого можна виключити випадкові коливання часового ряду, що досягається шляхом заміни значень у середині обраного інтервалу середньою арифметичною величиною.

Інтервал, величина якого залишається постійною, поступово зміщується на одне спостереження. Якщо спостерігається визначена циклічність змін показників, інтервал плинності має дорівнювати тривалості циклу. У разі відсутності циклічності у зміні показників рекомендується виконувати різноманітний розрахунок при параметрі згладжування, що змінюється. Кращий варіант визначається на основі подальшої оцінки вирівняних рядів.

За даними вирівняних значень ряду динаміки здійснюється підбір форми кривої, що відображає тенденцію розвитку явища. Отримане рівняння регресії використовується для визначення прогнозного значення досліджуваного показника.

Приклад 14.2

Розглянемо використання методу плинних середніх на підставі даних, наведених у табл. 14.6,

Таблиця 14.6. Вирівняні за плинними середніми значеннями товарних запасів підприємства, тис. грн

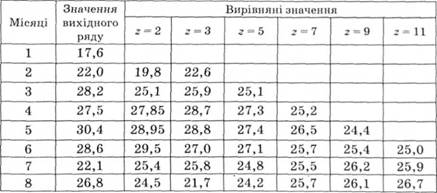
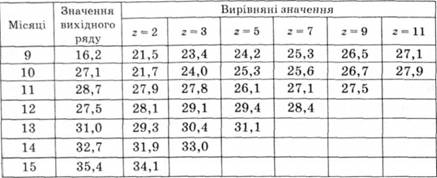
На основі вирівняних значень товарних запасів підприємства отримано такі значення коефіцієнта кореляції (г):

Наведені дані свідчать, що найкращі результати маємо за даними, вирівняними на основі 11 рівнів досліджуваного ряду динаміки.

У цьому випадку рівняння прямої матиме вигляд:

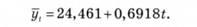
Використовуючи це рівняння, у перспективі отримуємо:

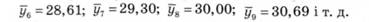
Прогнозне значення товарних запасів на 16-й рік можна визначити за формулою

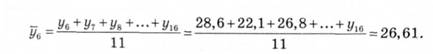
Звідси уи = 38,63 тис. грн.

Для розрахунку у17 використовується плинна середня у7, у формулі якої у1в буде вже відомою величиною.

Метод експоненціального згладжування

Експоненціальне згладжування - це вирівнювання динамічних рядів, що дуже коливаються, з метою наступного прогнозування. За цим методом можна дати обґрунтовані прогнози на підставі рядів динаміки, що мають помірний зв'язок у часі, і забезпечити більше врахування показників, досягнутих за останні роки. Сутність методу полягає у згладжуванні часового ряду за допомогою зваженої плинної середньої, у якій ваги підпорядковані експоненціальному закону. Кожне згладжене значення розраховується шляхом поєднання попереднього згладженого значення і поточного значення часового ряду. У цьому випадку поточне значення часового ряду зважується з урахуванням константи, що згладжує. Розрахунок здійснюється за формулою

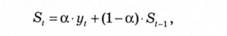
де ^ - значення експоненціальної середньої в момент *; у, - поточне значення ряду динаміки;

- значення експоненціальної середньої в момент (£ - 1); ос - константа, що згладжує.

Значення а завжди знаходиться в межах від 0 до 1, і в кожному конкретному випадку необхідно вибрати найбільш прийнятне значення.

Величину у формулі (14.9) можна також представити у вигляді суми фактичного значення рівня і згладженого значення спостереження, що йому передує £ 2, узятих із відповідними вагами. Процес такого поділу можна продовжити для членів ряду $^2$ і т. д. У результаті одержимо такий вираз:

у якому середнє згладжене значення є комбінацією всіх попередніх рівнів ряду. Величина у0 характеризує початкові умови процесу. Склавши у формулі (14.10) усі члени, що містять параметр а, одержимо:

де / - число періодів відставання від моменту £.

Відповідно до формули (14.11) відносна вага кожного попереднього рівня знижується за експонентою в міру його віддалення від моменту, для якого обчислюється згладжене значення. Звідси і виникла назва цього методу згладжування.

Послідовне застосування формули (14.10) дає можливість обчислити експоненціальну середню через значення всіх рівнів даного ряду динаміки. Крім того, вона визначає експоненціальні середні першого порядку, тобто середні, отримані безпосередньо при згладжуванні вихідних даних ряду динаміки. У тих випадках, коли тенденція після згладжування вихідного ряду визначена недостатньо чітко, процедуру згладжування повторюють, тобто обчислюють експоненціальні середні 2-го, 3-го і наступних порядків, користуючись такими виразами:

При практичному використанні методу експоненціального згладжування виникають деякі труднощі. Основними є вибір значення константи а і визначення початкової умови у0. Від чисельного значення параметра а залежить, наскільки швидко буде зменшуватися вага попередніх спостережень і відповідно до цього ступінь їхнього впливу на рівень, що згладжується. Чим більше значення параметра а, тим менше впливають попередні рівні і відповідно меншим виявляється вплив експоненціальної середньої. Пошук компромісного значення параметра згладжування становить задачу оптимізації моделі, що дотепер до кінця ще не вирішена.

Автор методу експоненціального згладжування, англійський учений Р.Г. Браун, запропонував таку формулу розрахунку а:

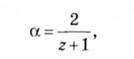
де г - число рівнів, що входять в інтервал згладжування.

Величина г визначається в цьому випадку емпірично.

Пошук оптимального значення параметра згладжування адаптивних поліномінальних моделей може здійснюватися також шляхом перебирання різних його значень. У цьому випадку оптимальним буде те значення а, при якому отримана найменша дисперсія помилки прогнозування, обчислена або при реалізації процедури згладжування всього ряду динаміки, або на не використаному в розрахунках відрізка ряду, який спеціально залишений для перевірки якості прогнозних моделей.

Завдання вибору параметра у0, що визначає початкові умови, пропонується вирішувати в такий спосіб:

o якщо є дані про розвиток явища в минулому, то замість у0 можна використовувати середню арифметичну всіх наявних рівнів ряду динаміки або якоїсь їхньої частини;

o якщо відомостей про розвиток явища в минулому немає, то замість у0 використовують вихідне (перше) значення рівня ряду Динаміки у. або спеціальні формули Брауна.

Для лінійної моделі початкові умови визначаються так:

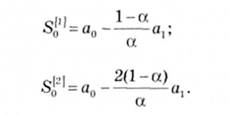
Для визначення значень коефіцієнтів а0 й ах необхідно розрахувати коефіцієнти рівняння тренду, отримані методом найменших квадратів.

Потім здійснюється розрахунок експоненціальних середніх першого і другого порядків за формулами (14.12), (14.13).

Прогноз у випадку лінійного тренду обчислюється за формулою

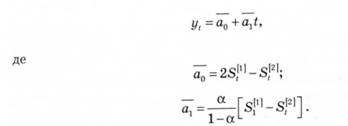
Помилку прогнозу можна обчислити за формулою

де а - середньоквадратична помилка відхилення від лінійного тренду, яка обчислюється за формулою

де к - число ступенів вільності, яке визначається за числами членів ряду п і параметрів вирівняної кривої.

Метод експоненціального згладжування порівняно з іншими методами прогнозу має переваги і недоліки. Серед переваг необхідно назвати його точність, що збільшується зі збільшенням числа рівнів динамічного ряду. Недоліком методу є те, що немає точного методу для вибору оптимальної величини параметра згладжування а. Точність прогнозу за цим методом зменшується зі збільшенням прогнозного інтервалу. Він ефективний для короткострокових прогнозів, в інших умовах його можна використовувати для одержання наближених оцінок.

Приклад 14.3

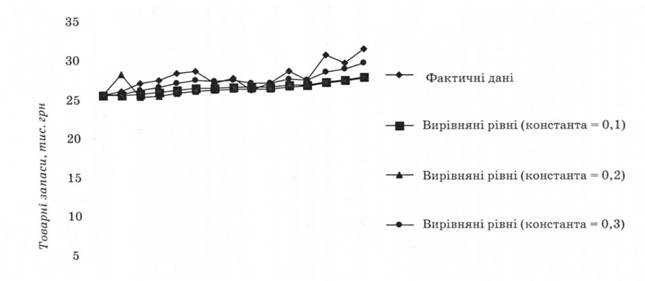
Складемо ретроспективний прогноз товарних запасів методом експоненціального згладжування для а = 0,1, а = 0,2 та а = 0,3 (табл. 14.7).

Розрахунок експоненціального згладженого значення здійснено за формулою (14.10), яка залежно від величини згладжу-вальної константи набуває вигляду:

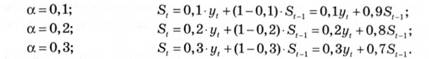
Незалежно від величини а експоненціальне згладжене значення у першому році дорівнює фактичному значенню рівня ряду динаміки за цей рік. Згладжене значення у наступних роках визначається так:

Аналогічно розраховуються і наступні згладжені значення, наведені в табл. 14.7.

Таблиця 14.7. Експоненціальні середні, розраховані за товарними запасами підприємства, тис. грн

Як видно з рис. 14.9, значення, отримані при а = 0,3, найкраще відображають загальний тренд.

Для розрахунку прогнозного значення залишку товарних запасів необхідно визначити експоненціальну середню другого порядку за формулою (14.12), а також параметри лінійного тренду за формулами (14.19) та (14.20).

Експоненціальна середня першого порядку для 16 місяця визначається за формулою (14.9), де поточне значення товарних запасів розраховане на підставі рівняння тренду:

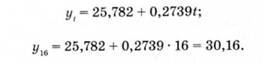
Результати розрахунків наведені в таблиці 14.8.

Таблиця 14.8. Побудова моделі прогнозу методом експоненціального згладжування

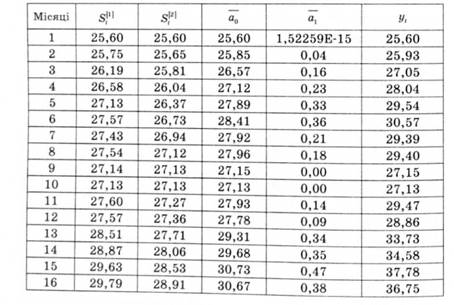
Таким чином, прогнозне значення залишку товарних запасів на 16-й місяць дорівнює 30,67 тис. грн.

Більш раціональним способом дисконтування інформації є метод гармонійних ваг, розроблений польським статистиком 3. Хелвігом. Він подібний до методу простого експоненціального згладжування і використовує той самий принцип. У його основі лежить зважування плинного показника, але замість плинної середньої використовується ідея плинного тренду. Екстраполяція проводиться за плинним трендом, окремі точки ламаної лінії зважуються за допомогою гармонійних ваг, що дає змогу пізнішим спостереженням надавати більшу вагу.

Метод гармонійних ваг базується на таких передумовах:

1) період часу, за який вивчається економічний процес, має бути досить тривалим, щоб можна було визначити його закономірності;

2) вихідний ряд динаміки не повинен мати стрибкоподібних змін;

3) прогнозоване соціально-економічне явище має бути інерційним, тобто для настання великої зміни в характеристиках процесу необхідно, щоб пройшов значний час;

4) відхилення від плинного тренду мають випадковий характер;

5) автокореляційна функція, розрахована на основі послідовних приростів, повинна зменшуватися зі зростанням часу (0" тобто вплив більш пізньої інформації має сильніше відображатися на прогнозованій величині, ніж на ранній інформації.

Для здійснення прогнозу за цим методом вихідний ряд динаміки розбивається на фази г. Число фаз має бути меншим за число членів ряду л, тобто г < п. Звичайно фаза г дорівнює 3- 5 рівням.

Для кожної фази розраховується лінійний тренд:

Для оцінки параметрів зв'язку використовується спосіб найменших квадратів.

За допомогою отриманих (п - г + 1) рівнянь визначаються значення плинного тренду (і/,(/)), з яких знаходиться середнє значення (уІ(п) за формулою арифметичної простої.

Для перевірки гіпотези про те, що відхилення від плинного тренду є стаціонарним процесом, розраховується автокореляційна функція. Якщо значення автокореляційної функції зменшуються від періоду до періоду, то п'ята передумова цього методу виконується.

Далі розраховують прирости за формулою

Середній приріст обчислюється за формулою

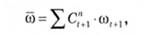
де С"+1 - гармонійні коефіцієнти за таких умов:

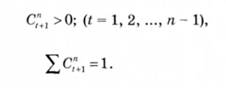
За цим виразом пізнішій інформації надається більше ваги, тому що прирости обернено пропорційні часу, який відокремлює ранню інформацію від пізньої для моменту і - п.

У загальному вигляді ряд гармонійних ваг визначають за формулою

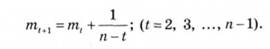
Щоб одержати гармонійні коефіцієнти С(я+1, які задовольняють умови (14.28), потрібно гармонійні ваги гпІ+ї розділити на (п -1), тобто

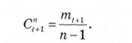
Далі прогнозування здійснюється так само, як і при простих методах прогнозу, шляхом додавання до останнього значення ряду динаміки середнього приросту, тобто

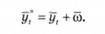
Приклад 14.4

Проілюструємо цей метод на прикладі динаміки реалізації продукції за 9 місяців 2007 р. (табл. 14.9).

Таблиця 14.9. Вихідні дані та результати розрахунку прогнозу обсягу реалізації продукції методом гармонійних ваг

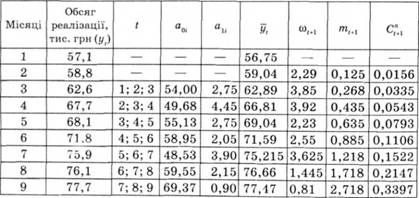
Попередньо ряд динаміки був перевірений на виконання передумов, на яких базується метод.

Параметри рівнянь окремих фаз руху плинного тренду визначені методом найменших квадратів за умови, що інтервал згладжування (г) дорівнює 3.

За допомогою отриманих рівнянь визначаємо значення плинного тренду.

Якщо г = 1, маємо одне значення у1{і)і яке отримуємо з рівняння

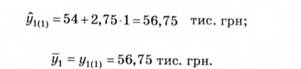
Якщо І - 2, маємо два значення дт, які отримуємо з рівнянь:

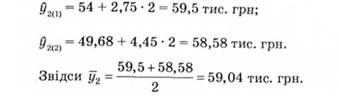
Якщо і = 3, маємо три значення уЮ), які отримуємо з рівнянь:

Аналогічно знаходимо всі значення у,.

Розрахунок приросту здійснюється за формулою (14.26). Наприклад:

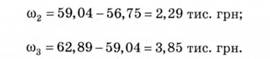
Гармонійні ваги визначаються за формулою (14.29). Наприклад:

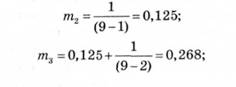
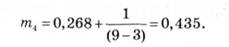
Гармонійні коефіцієнти отримуємо за формулою (14.30):

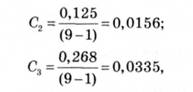
і так далі.

Використовуючи формулу (14.27), знаходимо середній абсолютний приріст (б) = 1,974) і розрахуємо прогнозні значення виробництва реалізованої продукції на наступні три місяці за формулою (14.31):

Цей метод прогнозування використовується тоді, коли є впевненість, що тенденція у майбутньому описується плавною кривою, тобто ряд динаміки немає сезонних і циклічних коливань.