Концепції сучасного природознавства - Карпов Я. С. - 2.8.3.3 Закон всесвітнього тяжіння

Ще в давнину, спостерігаючи за рухом планет, люди здогадувалися, що всі вони, разом із Землею, рухаються навколо Сонця. Пізніше, коли було забуто, про що знали колись, це відкриття заново зробив Коперник. І тоді виникли нові запитання: як саме планети рухаються навколо Сонця" який характер їхнього руху? Чи рухаються вони по колу й Сонце знаходиться в центрі, чи вони рухаються по якійсь іншій кривій? Як швидко вони рухаються? І так далі. З'ясувалося це не так швидко. Після Коперника знову настали неспокійні часи й розпочалися суперечки про те, чи обертаються планети разом із Землею навколо Сонця, чи Земля знаходиться в центрі Всесвіту. Тіхо Браге знайшов вихід із скрутного становища, що склалося на той час. Він прийшов до висновку, що потрібно дуже уважно стежити, де з'являються на небі планети, точно записувати дані спостережень і тоді уже вибирати між двома супротивними теоріями. Це і було початком сучасної науки, становленням нових підходів до правильного розуміння природи — спостерігати за явищем, записувати всі подробиці й використовувати їх для того чи іншого теоретичного тлумачення. І от Тіхо Браге у своїй обсерваторії фіксував щоночі положення планет. Величезну кількість високоточних даних Браге заповідав Кеплеру, який і спробував дати відповідь на питання, як рухаються планети навколо Сонця. У кінцевому підсумку Кеплер установив, що планети рухаються навколо Сонця по еліпсах, а Сонце знаходиться в одному з фокусів. Потім він відкрив другий і третій закони, які названі його ім'ям. Ці три закони вичерпно описують рух планет навколо Сонця. Але яка сила змушує планети рухатися?

Тим часом Галілей досліджував закони руху звичайнісіньких предметів, що були в нього під рукою. Вивчаючи рух кульки по похилій площині, хитання маятника й т.д., Галілей відкрив принцип інерції, відповідно до якого, якщо на предмет ніщо не діє і він рухається з певною швидкістю по прямій лінії, то рух відбуватиметься із цією ж швидкістю по цій же прямій лінії вічно.

Потім прийшов час Ньютона. Розмірковуючи над питанням: а якщо кулька не котиться по прямій лінії, що тоді? — він відповів так: для того, щоб хоч якось змінити її швидкість, потрібна сила. Наприклад, якщо ви підштовхнете кульку в тому напрямку, у якому вона котиться, то вона покотиться швидше. Якщо ви помітили, що вона повернула вбік, значить сила діяла збоку. Силу можна охарактеризувати добутком двох величин — прискорення й маси тіла. Силу можна і виміряти: наприклад, якщо ми прив'яжемо до мотузки камінь і почнемо крутити його над головою, то відчуємо, що мотузку треба тягти. Чим більша маса, тим сильніше потрібно тягти мотузку. Коли камінь рухається по колу, величина швидкості не змінюється, зате змінюється її напрямок. Ньютон вирішив, що планеті, яка обертається навколо Сонця, не потрібна сила, щоб рухатися вперед; якби ніякої сили не було, планета рухалася 6 по дотичній. Але насправді планета рухається не по прямій. її рух постійно відхиляється в бік Сонця. Щоб так викривити траєкторію, потрібна сила. Стало зрозуміло, що джерело цієї сили знаходиться десь біля Сонця. І Ньютонові вдалося довести, що другий закон Кеплера — закон рівності площ — безпосередньо випливає із тієї простої ідеї, що всі зміни у швидкості спрямовані до Сонця, навіть у випадку еліптичної орбіти. Цей закон посилив переконаність Ньютона в тому, що сила, яка діє на планет ти, спрямована до Сонця і що, знаючи, як період обертання різних планет залежить від відстані до Сонця, можна визначити, як слабшає сила з відстанню. Він довів, що сила оберненопропорційна квадрату відстані. Дотепер Ньютон не сказав нічого нового — він лише повторив іншими словами те, що сказав до нього Кеплер. Один закон Кеплера рівнозначний твердженню, що сила спрямована до Сонця, а інший — твердженню, що сила оберненопропорційна квадрату відстані й не залежить ні від яких інших величин, крім відстані.

Вихідний факт, покладений в основу Ньютонової теорії тяжіння, — вага, яку мають всі тіла, що знаходяться на Землі. З рівності прискорення для всіх падаючих тіл, доведеної численними експериментами, Ньютон встановлює, що ваги тіл, рів-новіддалених від центра Землі, відносяться як кількості матерії, чи маси тіл. За умови однакової віддаленості від центра Землі сили, з якими тіла притягають до себе Землю, відповідно пропорційні масам. Звідси випливає, що сила тяжіння, властива конкретному тілу, складається із сил тяжіння його частин. Тому всі земні тіла притягаються одне до одного із силою, пропорційною кількості матерії, тобто масі кожного тіла.

Установивши властивості земної ваги, Ньютон поставив за мету визначити тяжіння в небесному просторі. Як було зазначено вище, сила, що є причиною доцентрового прискорення планети, спрямована, як і саме прискорення, до Сонця, інакше кажучи, ця сила притягає планету до Сонця. Вона дорівнює прискоренню, помноженому на масу. З іншого боку, вага, що надає тілам рівномірного прискорення, спрямована до центра Землі й пропорційна масі. Ньютон припустив, що йдеться не про аналогію, а про тотожність, тобто ототожнив рух небесних тіл з падінням вантажів на Землі.

Установивши цей факт, Ньютон завершив об'єднання астрономії і земної механіки. Усю геніальну сміливість цієї ідеї важко зараз оцінити, настільки глибоко ввійшов закон всесвітнього тяжіння в науку.

Згодом Ньютон досліджує, чи можна за допомогою астрономічних спостережень підтвердити обернену пропорційність між квадратами відстаней і доцентровим прискоренням. Він припустив, що Місяць на орбіті утримують ті ж сили, що притягають предмети до Землі. Взявши за основу астрономічні дані, Ньютон підрахував, наскільки відхиляється Місяць за секунду від прямої лінії, по якій він повинен був би рухатися, якби його не притягувала Земля. Ця величина дещо більша, ніж 1,25 мм. Місяць знаходиться в 60 разів далі від центра Землі, ніж ми. Отже, якщо закон оберненої іропорційної залежності від квадрата відстані є вірним, то предмет біля поверхні Землі при падінні повинен пролітати за секунду 1,25 • 602, тому що на орбіті Місяця предмети притягаються в 60-60 разів слабкіше. Отже, 1,25 602 — це приблизно 5 м. Вимірювання Галілея показали, що, падаючи біля поверхні Землі, тіла пролітають за секунду 5 м. Це означало, що Ньютон на вірному шляху, тому що якщо раніше були відомі два незалежних факти: по-перше, період обертання Місяця й величина його орбіти і, по-друге, відстань, яку пролітає тіло, падаючи біля поверхні Землі, — то тепер ці факти виявилися тісно пов'язаними.

Таким чином, доцентрова сила, яка впливає на рух Місяця, на поверхні Землі повинна була б дорівнювати силі ваги. Сила, з якою Земля притягує Місяць і спричинює його рух по криволінійній орбіті, є земна сила ваги, дія якої поширюється аж до Місяця.

Якщо Земля притягує Місяць, то і Місяць з такою ж силою притягує Землю. З кеплерівських законів обертання планет навколо Сонця випливає, що доцентрова сила планет спрямована до центра Сонця, а доцентрова сила супутників — до центрів планет; ці сили оберненопропорційні квадратам відстаней до центрів тяжіння. Таким чином, закон тяжіння пояснює також рух планет і їхніх супутників. Досліджуючи рух комет, припливи й т.д., Ньютон в усьому бачить підтвердження свого закону.

Пізніше він переходить від небесних тіл до мікросвіту й прагне довести, що дрібні частинки речовини також зазнають взаємного тяжіння, яке пропорційне їх масі. Учений стверджує, що всі, без винятку, тіла — від нерухомих зірок до дрібних частинок — зазнають тяжіння, величина якого пропорційна добутку їхніх мас та оберненопропорційна квадрату відстані. Земля притягує Місяць, але і її саму притягує Сонце, і все це доповнюється зворотним впливом Місяця на Землю, Землі на Сонце й т.д. Відповідно, формула доцентрового прискорення перетворюється на формулу взаємного тяжіння

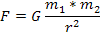
де G - множник пропорційності, а

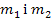— маси тіл, які взаємно притягаються одне до одного.

Віддаючи данину генію Ньютона, усе-таки слід зазначити, що закон всесвітнього тяжіння має ряд недоліків: він неспроможний, коли йдеться про обчислення руху Меркурія, передавання тяжіння через порожнечу, він визнає необхідність першого поштовху. На що "тірокляті питання" старої механіки дала відповідь загальна теорія відносності.